Каледин
В.О., Нагайцева Н.В.
Новокузнецкий
институт (филиал) Федерального государственного бюджетного образовательного
учреждения высшего профессионального образования «Кемеровский государственный
университет»
Методика и программная реализация аппроксимации
диаграммы деформирования органопластика при одноосном растяжении
Была выполнена серия экспериментов на девяти
одинаковых плоских прямоугольных образцах толщиной 4 мм, шириной 30 мм при
расстоянии между захватами разрывной машины 155 мм. Образцы изготовлены из
органопластика, армированного тканью ТСР 3 на связующем ЭДН-1У.
Эксперименты производились путем одноосного
растяжения с постоянной скоростью деформации до разрушения. После разрушения
образец выдерживался в испытательной машине в течение одной минуты.
Регистрировались диаграммы деформирования и температурные поля.
Вид диаграммы деформирования приведен на рисунке
1.
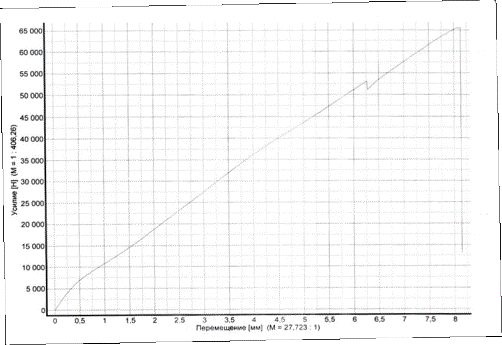
Рисунок 1 – Диаграмма «усилие-перемещение» для образца из
органопластика
Представленная диаграмма имеет следующие
особенности, характерные для данного материала. При малых нагрузках рост
перемещений происходит относительно медленно, что соответствует упругому
деформированию с начальным модулем упругости. При дальнейшем нагружении
касательный модуль упругости (тангенс угла наклона касательной к диаграмме)
уменьшается, а затем незначительно увеличивается и остается постоянным до
начала разрушения. На третьем этапе нагружения на диаграмме появляются
характерные зубцы, соответствующие локальным разрушениям, однако эти зубцы наблюдаются
не у всех образцов одной и той же серии. На последнем этапе нагружения
происходит разрушение образца, и нагрузка падает до нуля.
Аппроксимация диаграммы деформирования выбрана
так, чтобы по возможности точно описать уменьшение касательного модуля упругости
в процессе нагружения. Схема, иллюстрирующая построение аппроксимирующей
функции, приведена на рисунке 2.
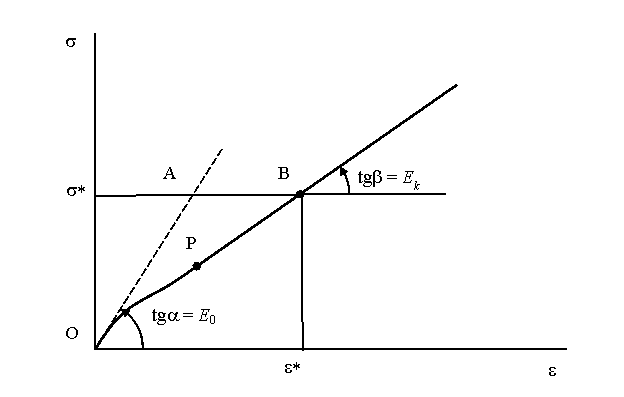
Рисунок 2 – Схема построения аппроксимирующей функции
На этой схеме пунктиром показана линейная
диаграмма деформирования с модулем упругости, равным начальному (отрезок ОА).
Кривая ОР аппроксимирует нелинейный участок диаграммы деформирования. Прямая PB
соответствует третьему этапу нагружения (линейный участок с постоянным
касательным модулем).
Начальный участок диаграммы (прямая ОА) имеет
уравнение:
![]() , (1)
, (1)
где
E0 – начальный модуль упругости.
На третьем участке диаграммы линейное уравнение
имеет вид:
![]() , (2)
, (2)
где
Ek – касательный модуль
упругости, ![]() и
и ![]() – координаты точки
линеаризации на диаграмме, показанные на схеме (рисунок 2). Между первым и
третьим участками диаграмма деформирования нелинейна. Для её описания
предлагается использовать решение линейного дифференциального уравнения второго
порядка с отрицательными корнями характеристического уравнения k1 и
k2:
– координаты точки
линеаризации на диаграмме, показанные на схеме (рисунок 2). Между первым и
третьим участками диаграмма деформирования нелинейна. Для её описания
предлагается использовать решение линейного дифференциального уравнения второго
порядка с отрицательными корнями характеристического уравнения k1 и
k2:
![]() (3)
(3)
с
начальными условиями:
![]() . (4)
. (4)
Правую часть выберем так, чтобы третий участок
диаграммы (прямая РВ) был асимптотой графика решения, т.е. чтобы функция![]() была частным решением уравнения (3). Подставляя это решение в (3), получаем
окончательный вид дифференциального уравнения:
была частным решением уравнения (3). Подставляя это решение в (3), получаем
окончательный вид дифференциального уравнения:
![]() . (5)
. (5)
Общее
решение уравнения (5) имеет вид:
![]() . (6)
. (6)
При
увеличении деформации решение должно асимптотически приближаться к линейной
функции, т.е. обе экспоненты в (6) должны стремиться к нулю. Поэтому корни
характеристического уравнения k1 и k2 должны быть
различными и отрицательными. Введем вспомогательный безразмерный параметр s –
положительное число, меньшее единицы, и выразим через него требуемые корни:
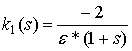 ,
, 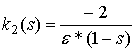 . (7)
. (7)
Рекомендуется выбирать s в диапазоне от 0,2 до
0,8.
Постоянные интегрирования C1, C2 определим из
начальных условий (4). Подстановка в (4) общего решения (6) с учетом (7) дает
следующие формулы для определения постоянных интегрирования:
 , (8)
, (8)
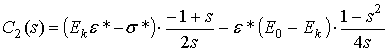 . (9)
. (9)
Дифференцируя
функцию (6), аппроксимирующую диаграмму деформирования материала, получим
зависимость касательного модуля от деформации:
![]() . (10)
. (10)
Нетрудно проверить, что при равенстве деформации
нулю модуль упругости равен начальному модулю E0, а при стремлении
деформации к бесконечности он асимптотически стремится к касательному модулю Ek.
Построенная таким образом аппроксимация
диаграммы деформирования содержит четыре настроечных параметра: координаты
точки линеаризации ![]() и
и ![]() ,
начальный модуль упругости E0 и касательный модуль упругости Ek.
Эти величины должны определяться из экспериментов, по диаграмме деформирования.
Целесообразно выбирать точку линеаризации на третьем участке диаграммы.
,
начальный модуль упругости E0 и касательный модуль упругости Ek.
Эти величины должны определяться из экспериментов, по диаграмме деформирования.
Целесообразно выбирать точку линеаризации на третьем участке диаграммы.
Вычисление начального модуля упругости
производится по формуле:
![]() , (11)
, (11)
где
![]() – угловой коэффициент диаграммы
«нагрузка-перемещение», Н/мм;
– угловой коэффициент диаграммы
«нагрузка-перемещение», Н/мм;
l,
b, h – соответственно длина, ширина и толщина образца в мм.
Вычисление
по формуле (11) дает модуль упругости в МПа.
Аналогично по угловому коэффициенту линейного
участка диаграммы может быть вычислен касательный модуль.
Для оценки точности аппроксимации (и для
дальнейших расчетов) рекомендуется использовать специально разработанную
компьютерную программу. Работа с аппроксимацией диаграммы деформирования в ней
производится на вкладке «Диаграмма деформирования» (рисунок 3).
Работа с компьютерной программой включает
задание первичных исходных данных, расчет (или ручное задание) параметров
диаграммы, а также расчет и построение графиков, показанных на рисунке 3.
При вводе координат точек диаграммы нагружения
могут быть использованы заранее подготовленные таблицы формата Excel или Word;
их содержимое копируется в буфер обмена и вставляется в таблицу «Данные
«перемещение-сила»» на форме. Удобнее, однако, вводить эти данные
непосредственно в таблицу. Удобство достигается тем, что пользователь может
выбрать один из вариантов задания данных: либо самостоятельно переводя
координаты точки машинограммы в миллиметры перемещений и килоньютоны, либо
вводя измеренные координаты в миллиметрах машинограммы. В последнем случае
перевод осуществляется по масштабам, напечатанным на машинограмме. Масштабы
должны быть введены в соответствующие поля на левой панели формы (рисунок 3).
После ввода первичных данных следует нажать
кнопку «Завершить ввод», после чего можно проводить расчет параметров
диаграммы.
Кнопка «Подбор» внизу левой панели позволяет
выполнить автоматический расчет параметров диаграммы по условию минимума
отклонения аппроксимирующей кривой от заданных первичных точек. В качестве
точки линеаризации выбирается средняя из заданных первичных точек. Результаты
расчета отображаются на графиках, расположенных на правой панели.

Рисунок 3 – Вкладка «Диаграмма деформирования»
Наличие зубцов на диаграмме снижает качество
вычислений. Целесообразно удаление соответствующих строк из первичной таблицы;
для этого следует использовать всплывающее контекстное меню.
Автоматический расчет недостаточно надежен и
может привести к значительной погрешности в определении начального модуля
упругости. Поэтому целесообразна ручная корректировка результатов. Для этого в
поля на левой панели следует ввести значения начального и/или касательного
модуля, определенные, как было описано выше, и нажать кнопку «Диаграмма
деформирования» для построения графиков при данных значениях параметров
аппроксимации. При необходимости следует откорректировать также координаты
точки линеаризации. Отклонение аппроксимирующей кривой от первичных точек можно
контролировать визуально по графику зависимости напряжений от деформаций
(второй сверху на рисунке 3), на котором сплошной кривой показана
аппроксимирующая функция, а точками – первичные данные.
Результатом обработки экспериментальных данных
являются значения начального и касательного модулей (поля на левой панели) и
графики зависимостей от деформаций следующих величин (сверху вниз): переменного
касательного модуля упругости (формула (10)), напряжений (формула (6)),
плотности рассеянной механической энергии на единицу объема и условной
температуры.