УДК 681.533.34

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СИСТЕМЫ С НЕЛИНЕЙНЫМИ ХАРАКТЕРИСТИКАМИ НА ПРИМЕРЕ ДОЗИРОВАНИЯ ЖИДКОСТИ

Сидоренко Сергей Александрович, Герасимов Роман Валерьевич, Маргарита Сергеевна Мелихова

Северо-Кавказский федеральный университет

Представлена математическая модель системы с нелинейными характеристиками для ее дальнейшего использования при моделировании системы управления на базе искусственных нейронных сетей.

Ключевые слова: управление, математическая модель, нелинейные характеристики.

Возрастающая необходимость в повышении энергоэффективности современных машин и агрегатов во всех областях промышленности обуславливает все более острую значимость применения интеллектуальных систем управления.

На сегодняшний день для решения этих задач ведутся работы по совершенствованию оборудования и использованию современных информационных технологий, но при этом управление нелинейными системами стараются свести к линейным, для которых существует мощный и удобный математический аппарат, позволяющий проводить их анализ и синтез, однако, все эти методы ограниченно приемлемы для нелинейных систем, например, для систем управления и регулировки гидроприводов.

В данной работе разработанна математическая модель процесса регулирования нелинейной системы на примере процесса дозирования жидкости.

Одним из аспектов решения проблемы дозирования жидкости является анализ влияния расходных характеристик на процесс истечения.

Анализ показал, что данная система имеет нелинейную зависимость расхода жидкости от положения управляющего элемента вследствие того, что несколько параметров изменяется нелинейно, например, площадь проходного сечения в регулирующем устройстве нелинейно зависит от изменения положения регулирующего элемента (задвижки, клапана и т. д.). Вследствие чего линейная аппроксимация передаточной функции системы управления приводит к неудовлетворительным результатам.

По результатам исследований на характеристики истечения через отверстия в тонкой стенке оказывают влияние следующие факторы: напор жидкости над сливным отверстием ; площадь отверстия ; плотность ; поверхностное натяжение ; вязкость жидкости и режим прохождения потока жидкости через отверстие (ламинарный или же турбулентный). Одним из наиболее сильно влияющих факторов на процесс истечения жидкости является площадь проходного сечения. [1].

В рамках данной работы определена зависимость между площадью проходного сечения и положением регулирующего элемента, в качестве которого выбран шаровой кран.

Для определения зависимости изменения площади проходного сечения от угла поворота сферы введены следующие ограничения:

- все поверхности имеют идеальные геометрическую форму и размеры;

- проходное сечение сводится к его проекции на плоскость;

- проходное сечение полностью определяет пропускную способность регулирующего устройства.

Помимо ограничений связанных с регулирующим устройством в работе при построении математической модели исключены факторы с наименьшим влиянием на процесс, а именно:

- поверхностное натяжение которое в случае истечения жидкости из отверстия при атмосферном давлении играет несущественную роль;

- переход из ламинарного в турбулентный режим при истечении через отверстия и насадки происходит постепенно, без резкого изменения коэффициента расхода.

С учетом вышеуказанных ограничений для определения зависимости площади проходного сечения от угла поворота сферического диска необходимо рассмотреть шаровой кран в сечении, проведенном по оси симметрии корпуса и перпендикулярно к оси рукоятки, схема которого представлена на рисунке 1.

Рисунок 1 – Сечение шарового крана

На рисунке 1: – диаметр отверстия в сфере; – угол поворота сферического диска относительно оси корпуса; – длина сферического диска.

Длина сферического диска, при соответствии крана ГОСТ 9544-93, имеет соотношение с диаметром отверстия, представленно в формуле 1.

, (1)

где – диаметр отверстия в сфере;

– длина сферического диска.

Для определения точки пересечения двух окружностей построим два треугольника и (рисунок 2). Треугольник является равнобедренным, так как . Рассмотрим треугольники и , данные треугольники равны по двум сторонам и углу между ними. Сторона равна стороне , сторона является общей стороной, угол равен углу и равен из треугольника . Рассмотрим треугольник , данный треугольник является равнобедренным, так как сторона равна стороне из условия равенства треугольников и . Следовательно, точка D принадлежит одновременно отрезкам , и находиться под углом к оси корпуса.

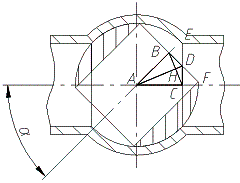
Рисунок 2 – Треугольники ABC и BCD

Определим отрезок , для этого рассмотрим треугольник :

.

Откуда следует, что:

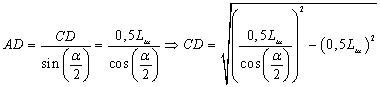. (2)

В дальнейшем вместо переменной используем переменную . Переменная является расстоянием, на котором расположена хорда относительно центра окружности, как показано на рисунке 3.

Рисунок 3 – Расположение хорды от центра окружности

Для определения дины хорды рассмотрим треугольник , представленный на рисунке 3. Из теоремы Пифагора следует:

.

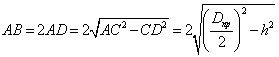Определим угол :

,

.

Тогда угол равен:

.

Определим площадь сегмента:

,

. (3)

Площадь сегмента является составляющей площади проходного сечения. Второй составляющей проходного сечения принимаем половину эллипса, получаемого в результате проецирования сегмента на плоскость, перпендикулярную оси корпуса (рисунок 4).

Площадь половины эллипса определяется по формуле:

, (4)

где – большая полуось;

– малая полуось.

Рисунок 4 – Вторая составляющая сечения

Из рисунков 3 и 4 видно, что в качестве большой полуоси можно принять половину хорды :

,

следовательно:

. (5)

Преобразуя формулу (5) и подставляя в нее значение длины сферического диска из формулы (1) получим:

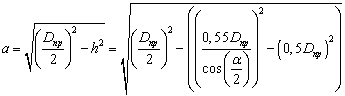. (6)

В качестве малой полуоси используем зависимость:

, (7)

подставляя в формулу (7) зависимость из формулы (2), получим:

. (8)

Подставляя в формулу (4) формулы (6) и (8), получим:

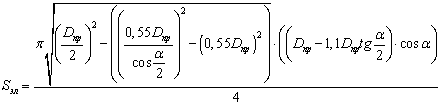. (9)

Площадь проходного сечения равна сумме площадей сегмента и половины эллипса:

, (10)

подставляя в формулу (10) формулы (3) и (9), получим:

, (11)

где – диаметр проходного отверстия шарового крана;

– угол поворота регулирующего элемента.

График зависимости площади проходного сечения от угла поворота диска шарового крана диаметром 20 миллиметров представлен на рисунке 5.

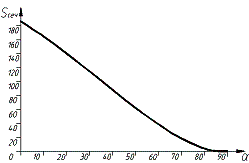
Рисунок 5 – График зависимости проходного сечения от угла поворота

После определения зависимости для проходного сечения задача сводится к определению скорости истечения и расхода жидкости.

Так при истечении жидкости из горизонтального отверстия на дне сосуда (рисунок 6) формула скорости будет иметь вид:

, (12)

где – ускорение свободного падения;

– напор жидкости над сливным отверстием.

При этом стоить отметить, что формула (12) будет справедлива только в том случае, если будет выполнено условие постоянства давления и стабильности уровня жидкости над отверстием. Данное условие выполнимо при избыточном поступлении жидкости в емкость и отводе лишней через специальные отверстия.

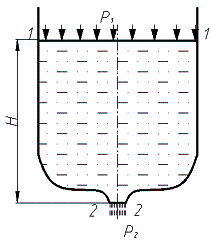
Рисунок 6 – Схема истечения жидкости

Зная скорость истечения и площадь проходного сечения, можно определить расход жидкости:

. (13)

Действительное явление, наблюдаемое при истечении жидкости из отверстия, несколько отличается от рассмотренной схемы, так как частицы жидкости в сечении отверстия движутся по непараллельным между собой траекториям, что обуславливает уменьшение площади поперечного сечения струи при выходе из отверстия [2]. В связи с этим действительный расход жидкости следует определять с учетом сжатия струи и действительной скорости истечения жидкости, а именно, вводя коэффициент расхода жидкости, который представляет собой отношение действительного расхода к теоретическому. Методика определения которого является темой для отдельного рассмотрения.

Таким образом, в результате работы:

- разработана математическая модель системы с нелинейными характеристиками на примере процесса истечения жидкости;

- обоснованна необходимость проведения экспериментального исследования для определения коэффициента расхода;

Разработанная математическая модель будет использована при создании управляющей системы дозирования жидкости на базе искусственной нейронной сети.

Литература

1. Гнедковский А. Н., Скобельцын Ю. А. Истечение жидкости через насадки при несовершенном сжатии // Изв. вузов. Нефть и газ, 1977. № 4. С. 73–77.

2. Идельчик И. Е. Справочник по гидравлическим сопротивлениям – 2-е изд. пер. и доп. – М.: Машиностроение, 1975. – 560 с.