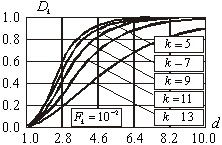Кревецкий Александр Владимирович

Обнаружение пространственных групп точечных объектов
на основе анализа графа иерархической группировки объемной сцены

Кревецкий Александр Владимирович

krevetskyav@volgatech.net

Поволжский государственный технологический университет,
Йошкар-Ола, Россия

Введение

В работе [1] показано, что наиболее информативными для распознавания пространственно компактных ГТО являются форма взаимного расположения точечных объектов, их число и плотность. Для выделения этих признаков необходимо вначале обнаружить, разрешить и пространственно ограничить ГТО.

Самые устойчивые к помехам (в виде ложных отметок и пропуска части полезных) известные методы обнаружения ГТО строятся на анализе плотности точек как некоторого их числа в области заданной формы [2, 3]. Такой подход оказывается недостаточно эффективным, когда форма данной области и ее ориентация заранее не известны.

В данной главе рассматривается метод обнаружения пространственно компактных ГТО, инвариантный к их форме и позволяющий разрешать и пространственно ограничивать ГТО при априорной неопределенности относительно ракурса наблюдения.

Математическая модель наблюдаемой точечной сцены

На рис. 1 приведен пример радиолокационного изображения, содержащего групповые малоразмерные объекты, сформированного радиолокатором с синтезированной апертурой. Из рисунка видно, что на изображении существуют отметки, схожие по размерам и яркости с отметками от реальных объектов и которые при обнаружении малоразмерных объектов могут быть приняты за них. Кроме того часть отметок от реальных объектов, например вследствие интерференции радиоволн могут иметь недостаточный контраст по отношению к окружению и вследствие этого быть пропущенными.

Рис. 1. Пример радиолокационного изображений ГТО

С учетом этого в качестве математической модели наблюдаемой точечной сцены рассматривается результат обнаружения точечных объектов:

, (1)

где x – пространственные координаты, – трехмерный символ Кронекера, – поле ложных точечных отметок с плотностью (ошибки первого рода), – поле сигнальных отметок с плотностью , – область пространственного ограничения ГТО (неизвестна), ― яркость n точки, и , ― координатный шум, i – номер класса ГТО.

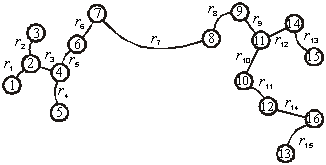
Используем для оценки пространственной компактности любых двух множеств точечных объектов меру на основе длин ребер графа иерархической группировки (рис. 2).

Рис. 2. Изображение дендрограммы иерархической группировки ГТО
в виде графа на плоскости исходной точечной сцены

Постановка задачи обнаружения пространственно компактных ГТО
с произвольной формой

Относительно наблюдения (1) выдвинем две альтернативные статистические гипотезы: 1) ― группа образована исключительно ложными отметками, 2) ― группа представляет собой смесь точек ГТО и ложных отметок.

Необходимо вынести обоснованное решение Н в пользу одной из данных гипотез, если условные относительно величины r распределения вероятности мощности k для групп из смеси точек ГТО и фона , а также групп исключительно из точек фона заданы. Здесь – длина ребра графа иерархической группировки точечных отметок, – пороговая длина ребра графа.

Пространственная локализация ГТО

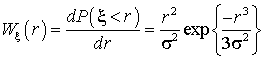Пусть – случайная длина ребра в графе иерархической группировки (рис. 2). Тогда для 3D равномерных полей точечных отметок получим следующие вероятностные модели: – вероятность непопадания в полушарие с радиусом r соседней отметки, – плотность случайного поля отметок, – плотность вероятности значений , (рис. 3), 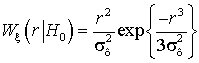, 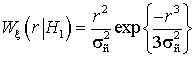– функции правдоподобия гипотез и , где – для области фона, для смеси фона и ГТО.

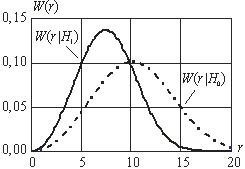
Рис. 3. Примеры распределения длин ребер минимального
дерева для равномерных полей точек

Байесовский алгоритм пространственной локализации ГТО на основе минимальной достаточной статистики имеет вид

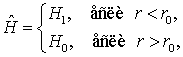
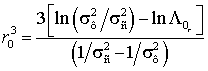, (2)

где – пороговое значение отношения правдоподобия , назначаемое согласно установленному критерию оптимальности, – и сводится к разрушению крупных (в статистическом смысле) ребер графа иерархической группировки на множестве точечных объектов наблюдаемой сцены.

Вероятности ошибок первого и второго рода для данного алгоритма определяются соответственно выражениями

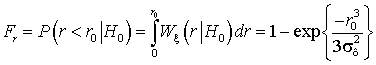, , (3)

В частности, оптимальный порог на длину ребра графа иерархической группировки для критерия Неймана-Пирсона может быть рассчитан по формуле .

Обнаружение 3D ГТО на фоне локализованных групп точек

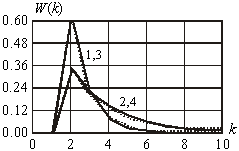
Статистические характеристики числа точечных отметок в локализованных на предыдущем этапе компактных группах описываются выражениями: , где , – распределение вероятностей, , – функции правдоподобия гипотез (рис. 4).

Рис. 4. Распределение вероятности мощности компактных групп

После формирования отношения правдоподобия и приведения подобных слагаемых получим оптимальный алгоритм обнаружения ГТО на основе минимальной достаточной статистики:

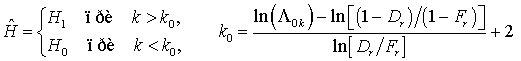, (4)

где – пороговое значение отношения правдоподобия. Как видно, алгоритм вносит решение об обнаружении ГТО по числу объектов в локализованных группах, превышающем величину .

Характеристики данного алгоритма для принятого в работе допущения о наибольшей априорной неопределенности относительно конфигурации ГТО можно рассчитать по формулам:

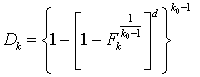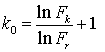, , где , . (5)

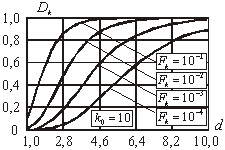
Hа pис. 5 пpиведены гpфики хаpактеpистик обнаpужения ГТО, pасчитанные согласно выpажению (5): рис. 5а – для четыpех фиксиpованных значений веpоятности ложных тpевог и фиксиpованного поpога . Хаpактеpистики на pис. 5б постpоены для и .

Рис. 5. Характеристики обнаружения ГТО с произвольной формой

Так, напpимеp, пpи интенсивности ложных отметок 200 на сцену размером 512х512, для обеспечения пpи достаточно, чтобы плотность отметок в области ГТО из не менее 10 малоразмерных объектов превосходила в 2,2 раза плотности ложных отметок.

Для оценки платы за незнание конфигурации ГТО сравним пороговые сигналы обнаружителя, реализующего алгоритм (2, 4) и обнаружителя ГТО с известным положением в исходной сцене и заданной формой области расположения [1]. Для занимаемого ГТО объема в 1000 элементов разрешения и рассмотренных выше плата за отсутствие априорной информацией о конфигурации ГТО станет приблизительно 40% увеличение порогового числа точек ГТО или соответствующее увеличение пороговой компактности отметок в области расположения ГТО.

Заключение

Рассмотренные в данной главе алгоритмы обнаружения ГТО имеют применение для случая, когда конфигурация ГТО, как один из наиболее информативных параметров, заранее неизвестна, но считается, что плотность отметок в области ГТО выше плотности ложных отметок.

Выбранная мера плотности точек учитывает особенности геометрии широкого класса ГТО и приводит к двухступенчатой процедуре обнаружения ГТО, где на первом этапе происходит оптимальная группировка точечных отметок по критерию минимального расстояния, а на втором – непосредственно обнаружение ГТО на основе анализа числа точек в каждой из выделенных на первом этапе групп. Анализ рассмотренных алгоритмов и результаты статистических экспериментов, проведенных путем моделирования на ЭВМ, демонстрируют удовлетворительное качество принимаемых решений в условиях сильной априорной неопределенности. Это обуславливает возможность применения обнаружителей, реализующих подобные алгоритмы, на этапе, предшествующем распознаванию ГТО, а также самостоятельно в условиях локационного наблюдения.

Достоинства описанного алгоритма обнаружения ГТО заключаются в следующем: 1) инвариантность к ракурсу наблюдения вследствие инвариантности алгоритмов локализации ГТО к данным преобразованиям, 2) инвариантность к форме и, следовательно, к номеру класса ГТО, поскольку точки группируются естественным образом по критерию компактности, 3) попутное формирование оцененок вторичных признаков ГТО, необходимых для последующего распознавания, 4) алгоритм является несмещенным равномерно наиболее мощным, в том числе и для сложной альтернативной гипотезы , когда известно лишь, что плотность объектов ГТО выше плотности ложных отметок.

Платой за отсутствие априорной информацией о конфигурации ГТО является приемлемое для практики увеличение порогового числа точек ГТО или соответствующее ему увеличение порога на длину ребра графа иерархической группировки.

Список литературы

1. Введение в контурный анализ; приложения к обработке изображений и сигналов/ Я.А. Фурман, А.В. Кревецкий, А.К. Передреев, и др.; Под ред. Я.А.Фурмана. – 2-е изд. – М.: ФИЗМАТЛИТ, 2003. – 592 с.

2. Комплекснозначные и гиперкомплексные системы в задачах обработки многомерных сигналов/ Я.А. Фурман, А.В. Кревецкий, А.А. Роженцов, и др.; Под ред. Я.А.Фурмана. – М.: ФИЗМАТЛИТ, 2004. – 456 с.

3. Krevetsky A.V. The Method of Associated Solid Image in the Theory of Groupp Point Objects Image Recognition// 8-th International Conference “Pattern Recognition and Image Analysis: New Information Technologies” (PRIA-8-2007): Conference Proceedings. Vol. 1. – Yoshkar-Ola, 2007. – P.324-326.