КЛАССИФИКАЦИЯ ГРУПП МАЛОРАЗМЕРНЫХ ОБЪЕКТОВ МЕТОДОМ АНАЛИЗА ПОСЛЕДОВАТЕЛЬНОСТЕЙ РЕБЕР МИНИМАЛЬНОГО ДЕРЕВА

Д. В. Уржумов, А. В. Кревецкий

Поволжский государственный технологический университет

Рассмотрена задача классификации групп малоразмерных объектов. Предложен алгоритм, анализирующий последовательности ребер минимального дерева. Доказана устойчивость к искажениям формы ассоциированного образа.

Введение

При анализе данных дистанционного зондирования актуальными задачами являются обнаружение и классификация искусственных объектов. Так как размеры подобных объектов близки к разрешению сенсора, форма их изображений вырождается [1]. На локационных изображениях, объекты с вырожденной формой выглядят как скачки яркости, состоящие из одной или нескольких смежных точек, и могут считаться точечными объектами (ТО).

Поскольку вырождение формы означает потерю наиболее информативной характеристики объекта, задача непосредственной классификации становится невыполнимой [2]. Распространенным походом к решению задачи классификации ТО является объединение их в группы (ГТО) и анализ ассоциированного сплошного изображения (АСО), полученного в результате такой группировки. Задача классификации ГТО осложняется как ошибками в результатах процедуры обнаружения ТО, так и отклонениями положения ТО от эталонного, вызванными особенностями рельефа на котором располагаются ТО или изменениями траектории движения ГТО (рис. 1).

Рис. 1. Пример искажений в ГТО типа цепочка.

Для повышения устойчивости алгоритма классификации ГТО к искажениям структуры АСО рационально использовать подход, учитывающий не только контур АСО, но и внутреннюю структуру ГТО.

Постановка задачи

Целью настоящей работы является разработка метода различения ГТО типов цепочка скопления по структуре минимального остового дерева (МД) – графа без циклов, построенного на входящих в ГТО ТО, как на вершинах.

Методика решения

Использование в качестве АСО МД, построенного на ТО, входящих в ГТО, как на вершинах, позволяет применить для анализа АСО помимо алгоритмов контурного анализа также методы теории графов. Положим – длину ребра, соединяющего смежные вершины v_i и v_j, МД равной геометрическому расстоянию между ТО, соответствующими вершинам v_i и v_j. Тогда длина маршрута , образованного последовательностью ребер равна 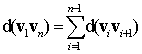. Для удобства будем считать, маршрутом в МД G, являющимся АСО для ГТО только последовательность попарно смежных вершин, степени которых: . Таким образом, граф G в силу своей ацикличности состоит из конечного множества не имеющих общих ребер маршрутов, границами которых будет множество V’ вершин v_j .

Пусть M_i – множество маршрутов, для которых вершина v_j, принадлежащая множеству V’ вершин МД G является граничной. Очевидно, что для сохранения структуры цепочки несмотря на искажения, внесенные смещениями образующих ТО относительно их эталонных положений, а также изменениями траектории движения ГТО, необходимо, чтобы суммарная длина побочных образовавшихся в результате различного рода искажений маршрутов по всем вершинам v_j, принадлежащих множеству V’, была значительно меньше суммарной длины основного маршрута. Пусть степень вершины v_k МД G , тогда из v_k существует p маршрутов . Примем справедливым соотношение: . Тогда множество будем считать множеством побочных маршрутов из вершины v_k. Обозначим сумму длин побочных маршрутов из вершины v_k как 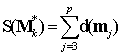. Сумму длин ребер u_j, принадлежащих множеству ребер U графа G, обозначим как . 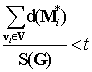Таким образом, ограничение на длину побочных маршрутов можно записать как , где t – пороговое значение. Экспериментально обнаружено, что для большинства ГТО типа цепочка: 0.01≤ t ≤ 0.1.

Полученные результаты

Поскольку предложенная методика анализирует отношение суммарной длины ребер побочной последовательности к общей суммарной длине ребер МД, алгоритм остается инвариантным к масштабированию и повороту АСО. Оценка суммарных длин позволяет исключить из рассмотрения геометрическое расположение ребер на плоскости относительно друг друга. Таким образом, предлагаемый алгоритм устойчив к искажениям, полученным в результате смене направления движения ГТО, приводящим к отклонению от эталонной формы АСО.

Предлагаемый алгоритм может быть осуществлен на этапе формирования МД. Производимый в рамках данного алгоритма анализ структуры МД может быть использован для построения контура АСО, состоящего из элементарных векторов (ЭВ), построенных на ребрах МД. Построенный подобным способом контур АСО содержит меньшее количество ЭВ. Таким образом, как трудоемкость самого алгоритма, так и дальнейших операций над АСО ниже чем при использовании методов, основанных исключительно на алгоритмах контурного анализа.

Заключение

Таким образом, предлагаемый алгоритм может быть применен при классификации ГТО. Хотя данный алгоритм требует исключительно АСО, представленного в виде МД, он более устойчив к искажениям структуры ГТО. Интеграция в процедуру построения МД, а также выполнение операций над контуром, содержащим оптимальное число ЭВ, повышает производительность алгоритма и позволяет ему функционировать в реальном масштабе времени.

Список литературы

1. Кревецкий А.В., Митрофанов В.И., Плекин В.Я. Различение групповых точечных объектов по форме ассоциированного сплошного образа // Известия вузов. Радиоэлектроника. – 1997, Том 40, №3.- С. 44-52.

2. Введение в контурный анализ; приложения к обработке изображений и сигналов/ Я.А. Фурман, А.В. Кревецкий, А.К. Передреев, и др.; Под ред. Я.А.Фурмана. – 2-е изд. – М.: ФИЗМАТЛИТ, 2003. – 592 с.

Работа выполнена в рамках проекта РФФИ № 13-01-00427