Приложения теории оптимального управления

к синтезу композиционных материалов

¹Будылина Е.А., ²Гарькина И.А., ²Данилов А.М.

¹Московский государственный машиностроительный университет

²Пензенский государственный университет архитектуры и строительства

Рассмотрим подход к синтезу материалов как к задаче управления и его приложения к оптимизации свойств и структуры композиционных материалов. Он состоит из указанных ниже этапов.

1. Техническая постановка задачи и выбор технического критерия оптимизации.

2. На основе технической постановки задачи строится математическая модель объекта управления в форме системы операторных уравнений (дифференциальных, интегральных, разностных, дифференциально-разностных, дифференциально-интегральных и т.д.). При этом математическая модель и пути ее построения зависят от степени изученности объекта, наличии опыта разработки аналогичных систем, полноты знания физических процессов, характеризующих поведение объекта, и строится на основе теоретических исследований по изучению физических процессов в системе, логического анализа, идентификации по данным нормальной эксплуатации и т.д. Далее делается оценка области применения математических моделей. Здесь же выбираются компоненты вектора управления, параметры системы и возмущения. Устанавливаются фазовые координаты, и строится пространство состояния объекта, указываются ограничения на компоненты вектора управления. Так, ограничения на фазовые координаты (например, установление допустимого угла атаки летательного аппарата) могут дать принадлежность вектора состояния некоторому замкнутому множеству точек -мерного пространства. Они могут определять прочность, жесткость объекта и т.д. Здесь же указываются ограничения на вектор управления (например, энергопотребление). Определяются начальные или краевые условия, осуществляется выбор критерия для оценки качества управления.

3. В предположении полной формализации задачи выбирается метод оптимизации. Как правило, предполагается задание математической модели объекта применительно к выбранному методу на его языке. Однако не исключается, когда модель подгоняется под выбранный метод оптимизации. Например, по системе дифференциальных уравнений линейного объекта может быть построен соответствующий функционал качества на основе корней характеристического полинома.

4. Выбор численных методов, реализующих метод оптимизации (методы решения систем дифференциальных уравнений, определения значений функционала качества и т.д.).

5. Разработка и отладка программно-алгоритмического обеспечения (в том числе корректировка численных методов для повышения точности и вычислительной эффективности алгоритма).

6. Анализ полученных результатов оптимизации с возможной корректировкой и упрощением, как всей математической задачи, так и отдельных ее элементов. Результаты решения математической задачи являются исходной информацией для уточнений формулировки технической задачи, и итерационный процесс может повторяться до достижения заданной точности.

Практически без оговорок указанная последовательность может использоваться при синтезе материалов из условий получения требуемых кинетических процессов формирования физико-механических характеристик материалов (прочность, твердость, параметры тепловыделения, химическая стойкость и т.д.). Основные понятия и определения материаловедения легко интерпретируются в соответствующих терминах, принятых в теории систем управления, часть из которых приводится ниже.

Линейные объекты с непрерывным временем описываются векторно-матричным уравнением состояния

;

(1)

- вектор фазовых координат (состояние объекта); - вход (управление объектом); - непрерывные матрицы, имеющие соответственно размерности . Выход объекта (т- символ транспонирования) в общем случае определяется в виде уравнения наблюдения

,

(2)

- непрерывная матрица размерности .

В общем случае объект описывается нелинейным дифференциальным уравнением

.

(3)

После линеаризации получим систему (1) - (2) (структурная схема на рис.1).

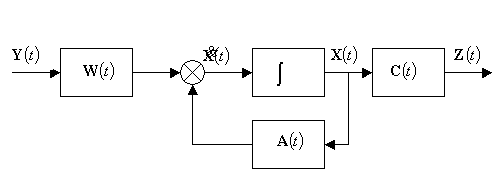
Рис.1.Структурная схема

В материаловедении управление структурой и свойствами материала осуществляется изменением соответствующих рецептурно-технологических параметров [1]. Из этого с очевидностью следует, что оптимизация структуры и свойств материала (объекта) возможна из условий получения оптимальных параметров кинетических процессов (критерии качества) изменением рецептурно-технологических параметров (управляющее воздействие).

Литература

1. Будылина Е.А., Гарькина И.А. Данилов А.М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. № 2(16). 2013. – C. 138-143.