Электродинамическая поправка сечения рассеяния сдвиговой волны

цилиндрической неоднородностью в пьезоэлектрическом кристалле

Е. Г. Косяк, Н. С. Шевяхов

Саровский физико-технический институт НИЯУ МИФИ

Последнее десятилетие ознаменовалось в ряде областей физики повышенным интересом исследователей к регулярно-периодическим композитным средам, иначе – икусственным квазикристаллическим образованиям, за которыми утвердилось общее название – метаматериалы. Наиболее широко исследуются свойства метаматериалов в оптике [1], где их также называют фотонными кристаллами. По аналогии с оптикой в акустике рассматривают фононные кристаллы. В простейшем варианте двухмерный фононный кристалл – это однородная упругая или жидкая среда, пронизанная упорядоченной системой одинаковых стержней или полостей.

Для приложений важно располагать удобной возможностью динамического манипулирования основным параметром фононного кристалла – шириной запрещенной зоны. В случае 2d-фононных кристаллов с жидкой матричной средой предлагался [2] механический способ управления посредством вращения прямоугольных стержней. Технологичнее, однако, применять управление внешними полями, оказывая на фононный кристалл статическое или импульсное электрическое воздействие. По указанной причине получили развитие фононные кристаллы с пьезоэлектрической матрицей [3].

Свойства фононных кристаллов определяются особенностями рассеяния акустических волн структурными элементами решетки. Соответственно фундаментальное значение имели и продолжают сохранять вопросы теории рассеяния акустических волн одиночными неоднородностями в материалах, используемых в фононных кристаллах в качестве матричной среды. Для пьезоэлектриков акустическое рассеяние рассматривается обычно [4, 5] в квазистатическом приближении. Ниже на примере рассеяния плоской монохроматической сдвиговой волны горизонтальной поляризации круговой вакуумной полостью в пьезоэлектрике класса 6mm, 4mm () будет показано, что с учетом запаздывания электрических полей полное поперечное сечение рассеяния приобретет электродинамическую поправку. Влияние ее мало, но может возрасти на несколько порядков в случае металлизации полости. Для теории фононных кристаллов на основе пьезоэлектриков можно также заключить, что в условиях их предельно высокой механической добротности именно электродинамический добавок к сечению рассеяния может оказаться источником не исчезающе малых потерь из-за большого числа актов рассеяния.

Примем, что полость не заполнена веществом и ориентирована осью вдоль оси симметрии высшего порядка пьезоэлектрика, занимающего в цилиндрических координатах область . Полагаем также, что сдвиговая волна со смещениями падает на полость нормально вдоль луча . В этих условиях рассеяние происходит без изменения поляризации волны и аналогично [5] из уравнений пьезоэффекта [4] имеем отличные от нуля компоненты тензора напряжений

(1)

и электрической индукции

(2)

где – модуль сдвига, пьезомодуль и диэлектрическая проницаемость пьезоэлектрика, – электрическая постоянная.

Для гармонических полей , , где – частота, – время, рассмотрение (1), (2) вместе с уравнениями Максвелла и уравнением движения упругой среды [4] показывает, во-первых, связь смещений с электромагнитным полем Н-типа , :

. (3)

Во-вторых, вытекающую отсюда возможность выражать поля в пьезоэлектрике величинами ,, которые определяются из уравнений Гельмгольца

. (4)

Аналогичным образом, электромагнитное поле в полости, возбуждаемое с ее поверхности колебаниями пьезозарядов, индуцируемых падающей волной, целесообразно характеризовать напряженностью магнитного поля , единственная составляющая которого также удовлетворяет уравнению Гельмгольца

. (5)

В выражениях (3)-(5) и – волновые числа сдвиговой и электромагнитной волн в пьезоэлектрике, – волновое число электромагнитной волны в вакууме, – скорость света, , – плотность.

Уравнения (4), (5) дополним граничными условиями

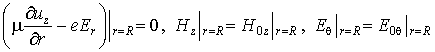. (6)

Первое из них выражает стандартное требование отсутствия механических напряжений на границе упругой среды с вакуумом [4]. Другие два представляют обычное для электродинамики условие непрерывности тангенциальных компонент электромагнитного поля на границе раздела сред в отсутствие свободных зарядов и токов.

Падающая сдвиговая волна не сопровождается вихревым электрическим полем. Поэтому с учетом ограниченности решения в полости и погашаемости полей на бесконечности из уравнений (4), (5) получим

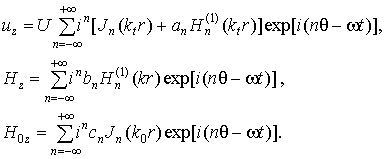(7)

Напомним, что первое слагаемое выражения (7) для величины представляет собой известное из теории цилиндрических функций [6] разложение падающей плоской волны в ряд по цилиндрическим гармоникам. Таким образом, под в (7) понимается полное поле, слагаемое падающей волной и всеми парциальными волнами, рассеянными полостью. При записи выражений (7) использованы общепринятые [6] обозначения функций Бесселя и Ханкеля целочисленного порядка .

Для определения коэффициентов подставим (7) в (6), где предварительно выразим величины и через согласно (3) и учтем, что . Образующаяся в итоге система неоднородных алгебраических уравнений дает

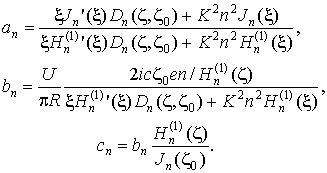(8)

В формулах (8) штрихами помечены производные цилиндрических функций, а также обозначено:– квадрат коэффициента электромеханической связи пьезоэлектрика, , , . Функция в (8) имеет вид

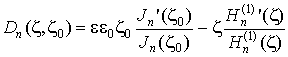. (9)

Сопоставим решение (7), (8) результатам работы [5]. Переход к квазистатическому пределу , когда согласно (9) , можно непосредственно выполнить для коэффициентов , принимающих, как следовало ожидать, вид работы [5]. Для остальных коэффициентов (8) необходима предварительная подстановка в (7), где наряду с условием выполняются условия и . В результате парциальные компоненты магнитных полей оказываются пропорциональными мультиполям потенциалов полей рассеяния квазистатического приближения [5], которые изменяются по степенному закону при и , если . Тождественность результатам [5] здесь состоит в том, что определяемая вихревая часть электрического поля (3) в пьезоэлектрике или связанное с вихревое электрическое поле в полости, совпадают при с электрическими полями указанных потенциалов.

Потенциалы мультиполей рассеяния локализуются у границы полости и не переносят энергию в радиальном направлении. Поэтому приходящееся на единицу длины полости (погонное) полное поперечное сечение рассеяния (ППСР) сдвиговой волны определялось в [5] только акустической частью

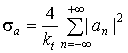. (10)

С учетом запаздывания переизлученное в результате рассеяния сдвиговой волны электромагнитное поле с магнитной компонентой и электрической частью, определяемой по формуле (3), обретает способность к радиальному переносу энергии. Формально на это указывает присутствие в выражении вектора Пойтинга для рассматриваемого случая

(11)

первого (электродинамического по происхождению) члена. Соответственно в выражении для ППСР к величине из (10) добавится подлежащая определению электродинамическая поправка .

Согласно общепринятому определению ППСР

. (12)

Угловые скобки здесь обозначают средние по времени величины, – радиус произвольного цилиндра, охватывающего полость, а – средний поток энергии, переносимый падающей волной [4]. Среднее значение радиального потока энергии можно представить на основании (11) в виде

, (13)

где звездочка – знак комплексного сопряжения. Чтобы получить , в выражении (13) следует брать не полную величину из (7), а только часть, относящуюся к рассеянному полю. С учетом этого обстоятельства, используя для определения и их сопряженных значений формулы (1), (3) на основании (12) получим после преобразований

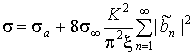, (14)

где – геометро-оптический предел ППСР, а .

В пьезоэлектриках обычно имеем , где – скорость сдвиговых волн. Оценку электродинамической поправки к ППСР целесообразно, поэтому, выполнять в области . Область практически соответствует квазистатическому пределу, когда и из (14) вытекает, что

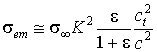. (15)

Для пьезокерамики с типичными параметрами , даже при замене в (15) на (таким формальным способом, обнуляя везде, кроме спектральной переменной , приходим к случаю металлизированной полости [5]) не превышает от уровня . Таким образом, использование в аналогичных условиях работы [5] квазистатического приближения представляется вполне оправданным.

Возможность увеличения из-за запаздывания электрического поля имеет смысл связывать с ростом отношения . Оговоримся, однако, что существенное возрастание , например, в сегнетоэлектриках в окрестности фазового перехода [7], сопряжено со столь же значительным уменьшением в (14) ввиду того, что знаменатель этих коэффициентов (8) содержит функцию , пропорциональную . В результате поправка остается весьма малой. Исключение представляет случай металлизированной полости в сегнетоэлектрике, когда в формуле (9) как выражение металлизации поверхности можно принять . Особенности возникающих в таких условиях изменений ППСР вследствие запаздывания электрического поля и пьезоэффекта иллюстрируют кривые зависимостей на рис. 1, рассчитанные по формулам (8), (9), (14) при .

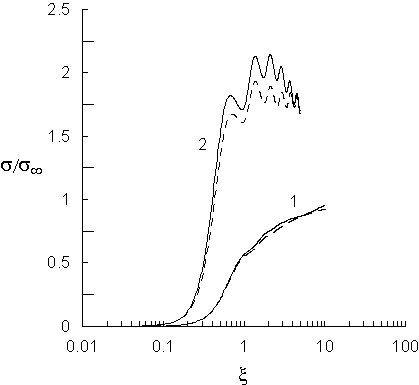
Рис. 1. Спектры ППСР: 1 – металлизированная полость сегнетоэлектрика; 2 – гипотетический пьезоэлектрик с аномально высоким запаздыванием в отсутствие металлизации полости. Штриховыми линиями показаны соответствующие спектры ППСР при отсутствии запаздывания электрического поля.

Кривые 2 на рис. 1 соответствуют рассеянию сдвиговой волны металлизированной полостью в сегнетоэлектрике () при условном значении параметра запаздывания (сплошная кривая) и отсутствии запаздывания (, штриховая кривая). Кривые 1 рассчитывались для неметаллизированной полости в гипотетическом пьезоэлектрике с параметрами и аномально высоким запаздыванием (сплошная кривая). Несмотря на это различие между сплошной и штриховой () кривыми 1, показывающее влияние запаздывания, выражено заметно слабее, чем это имеет место для кривых 2. Как уже отмечалось [5], мелкопериодическая рябь на кривых 2 обязана своим происхождением интерференционному вкладу в рассеяние электрозвуковой поверхностной волны, способной эффективно удерживаться металлизированной границей полости.

Рассмотрим теперь случай гиперзвуковых частот СВЧ-диапазона, освоенных в практике генерирования акустических колебаний в твердых телах. Здесь для типичных пьезоэлектриков с размерами полости имеем с допустимыми значениями . Можно предположить, что ввиду предельно больших ряд (14), если сходится, то прежде, чем возникнет потребность в учете членов номеров . Коэффициенты можно, поэтому, оценивать в (8) при (практически в пределе при ) с использованием асимптотических разложений функций Ханкеля аргумента [6]:

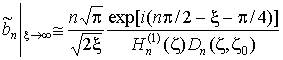. (16)

Из выражения (16), вообще говоря, вытекает, что на высоких частотах поправка оказывается пренебрежимо малой. Имеется, однако, принципиально отличие от случая низких частот. Именно, на частотах и при номерах цилиндрических гармоник, для которых функция оказывается существенно малой, может заметно возрасти. Так как функция характеризует в асимптотическом пределе парциальный импеданс полости для электромагнитного поля H-поляризации, то причину указанного различия нетрудно усмотреть в проявлении полостью свойств открытого резонатора электромагнитных колебаний.

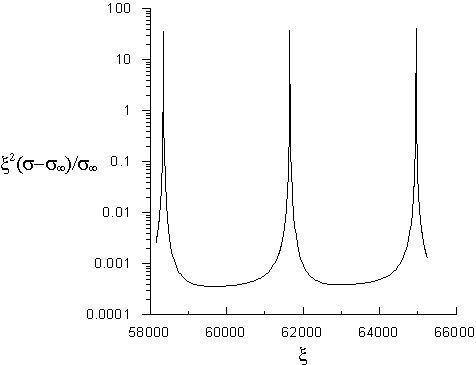
Рис. 2. Относительное изменение ППСР вследствие запаздывания электрического поля для резонансной области электромагнитных колебаний полости: .

Резонансы полости можно подавить, согласуя электрически полость с пьезоэлектриком. Для этого, например, достаточно разместить в полости без акустического контакта с пьезоэлектриком диэлектрический цилиндр с проницаемостью близкой . Принимая в (9) в связи с выравниванием поляризационных свойств полости и внешней среды , с учетом выражения для вронскиана [6] и ввиду равенства , придем на основании (14), (16) к оценке нерезонансного значения на высоких частотах

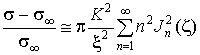
и поскольку 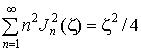, имеем оценку типа (15):

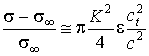. (17)

Для определения непосредственно в резонансах прибегнем к численному расчету по формулам (14), (16). Результаты вычислений подтверждают наличие острых резонансных пиков зависимости при и позволяют установить, что при обычных значениях область электромагнитных резонансов находится в окрестности значений . Типичный фрагмент зависимости , содержащий три первых резонансных пика, показан на рис. 2. Видно, что в резонансах величина возрастает на 5 порядков и выше, но в абсолютном выражении составляет, из-за существенно больших , ничтожно малую величину , согласующуюся с ранее данными оценками по формулам (15), (17). Отсюда заключаем, что если не принимать в расчет строгую подстройку в резонанс, не имеющую практического смысла по причине проявляющихся в реальных условиях потерь, то в обычных условиях электродинамическая поправка ППСР пренебрежимо мала и независимо от диапазона частот при вычислениях правомерно использовать квазистатическое приближение.

Литература

1. С. Е. Банков. Электромагнитные кристаллы. М.: Физматлит, 2010. 352 с.

2. C. Goffaux, J.P. Vigneron. Theoretical study of a tunable phononic band gap system // Physical Review. B. 2001. Vol. 64. P. 075118-1.

3. T. T. Wu, Z. C. Hsu, Z. G. Huang. Band gap and electromechanical coupling coefficient of a surface acoustic wave in a two-dimensional piezoelectric phononic crystal // Physical Review B. 2005. Vol. 71. P. 064303-1.

4. Д. И. Бардзокас, А. И. Зобнин, Н. А. Сенник, М. Л. Фильштинский. Математическое моделирование в задачах механики связанных полей. Т. II: Статические и динамические задачи электроупругости для составных многосвязных тел. М.: КомКнига, 2005. 376 с.

5. Н. С. Шевяхов. О полном сечении рассеяния поперечной волны полостью в гексагональных и тетрагональных пьезоэлектриках // Акустический журнал. 1998. Т. 44. № 6. С. 855-857.

6. Б. Г. Коренев. Введение теорию бесселевых функций. М.: Наука, 1971. 288 с.

7. Б. А. Струков, А. П. Леванюк. Физические основы сегнетоэлектрических явлений в кристаллах. М.: Наука, 1995. 304 с.