Òåõíè÷åñêèå íàóêè /12.Àâòîìàòèçèðîâàííûå ñèñòåìû óïðàâëåíèÿ
íà ïðîèçâîäñòâå.
Ph.D. Lyashenko A.
National mineral resources university
DEVELOPING SYSTEMS WITH OPTIMAL
ADAPTIVE TRANSFER FUNCTION
In many cases, the static and dynamic
properties of the systems change over
time, and the regulator with a
constant setting can not provide
the optimal condition. In these cases it is necessary to change the setpoint
setpoint or parameters of any elements, change the wiring diagram elements or introduce new elements: such as logic gates, computers,
and the elements of the automatic
search, which leads to the creation of automated systems with properties of self-adjustment or adaptation. In this
connection, in real time, the
development of the theory of automatic
control systems, and its practical application, is characterized by intensive
development of adaptive management. These techniques are used for construction of control systems with
significant uncertainties of the
control object and the conditions of its functioning (environmental characteristics), available at the design stage or before the commencement of operation
of the system. We
consider such management tasks for which the dynamic properties
of an object can vary widely
unknown in advance way. Available primary
(a priori) is not enough information
to build control systems with optimal (or given) quality
indicators. In adaptive control systems, the lack of a priori information compensated during its operation on
the basis of the current data on
the behavior of the object. These
data are processed in real time (the
flow rate control process) and used to improve the quality control system.
Application of the principles of adaptation
allows you to:
- To ensure the system is operating in a significant change in the dynamic properties of the object;
- To make optimization of operating modes of the object by changing its parameters;
- To reduce the technological
requirements for the construction of
individual components and elements of the system;
- To unify separate controls or blocks of regulators, adapting them to work with
different kinds of similar objects;
- Shorten design
tests;
- To increase system
reliability.
Widespread in practice the task is to stabilize the dynamic properties of industrial objects for which the transients are considered primary modes of operation.
Under the influence of random factors
and due to changes in the parameters of the system may be in breach of these regimes. Stabilization of transients can be done by comparing the timing of objects with
some reference to the subsequent minimization of their differences. The
objective being to achieve optimal accuracy and optimal
performance under varying environmental
conditions and characteristics of the object. Here, the
best solution is obtained using adaptive
systems.
Consider the process of
adaptation in the presence of the
reference model (Fig. 1) as an
example of thermal processes.
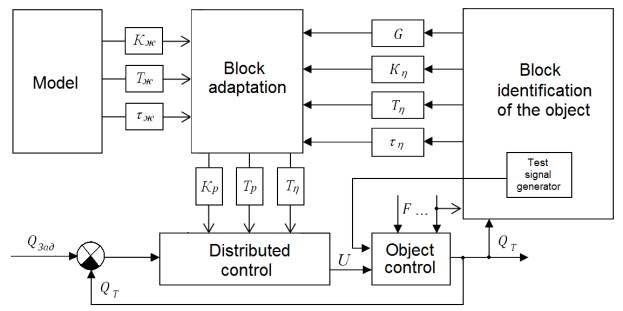
Fig. 1. A block diagram of an adaptive system model
Thermal processes in objects with distributed
parameters (PPR) can be described
by the following transfer function
[1]:
 (1)
(1)
where: 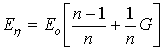 – the gain of the
object;
– the gain of the
object;
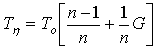 – time constant; G – generalized coordinate; τη
–
– time constant; G – generalized coordinate; τη
–
time lag,
n – a
weighting factor..
The transfer function of the synthesized distributed PID controller according to [2] is:
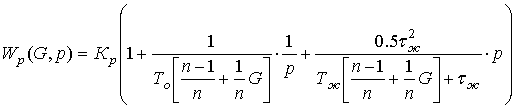 (2)
(2)
We introduce the notation and write the
expression:
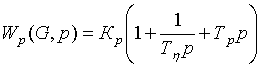 (3)
(3)
where: 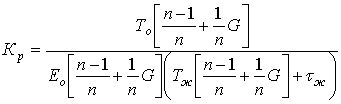 ; (4)
; (4)
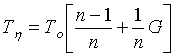 ; (5)
; (5)
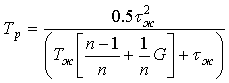 . (6)
. (6)
The model specifies the desired values
of the transfer, the
time constant and the time delay
of the control object.
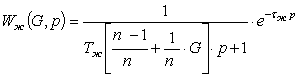 . (7)
. (7)
With the identification
of the object management unit
define the parameters ![]() the results of numerical
simulations. For this test
signal generator generates
and supplies the input to the
system input action of the form:
the results of numerical
simulations. For this test
signal generator generates
and supplies the input to the
system input action of the form:
![]() (8)
(8)
where: ![]() ;
; 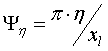 ;
; ![]()
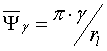 .
.
According to the results of
numerical simulations we define
the parameters ![]() , which is input adaptation
unit.
, which is input adaptation
unit.
Adaptation unit calculates the
controller parameters in accordance with a specially developed technique. This uses the expression (4) - (6).
Adaptation procedure can be represented
as a block diagram in Fig. 2.
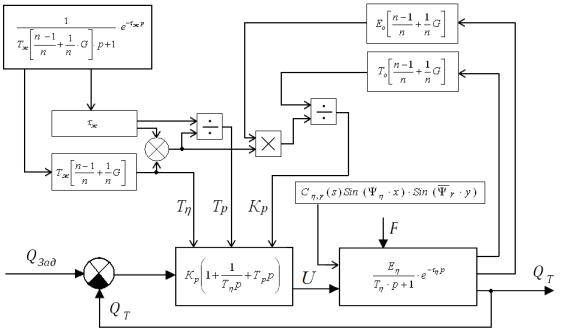
Fig. 2. A block
diagram of an adaptive system model
Using this method, we calculated the settings adaptive distributed PID control system for
thermal fields thermohousing protective circuit television camera. The simulation results of the closed system management demonstrated the high quality management of
the facility in full accordance
with the requirements of the
control system.
Literature
1. Pershin I.M. The analysis and synthesis of systems with distributed
parameters. - Pyatigorsk, RIA at CMS. 2007. - 244c.
2. Lyashenko A.L. Development of methods for the synthesis of optimal
control of distributed systems / Components and Technology - 2013. - ¹ 2 (139).
- c. 122-124.