5. Технические науки

Іванов В. І., Скачков В. О., Мосейко Ю. В.

Запорізька державна інженерна академія

ТЕРМОДИНАМІЧНІ ОСНОВИ МАТЕМАТИЧНОЇ МОДЕЛІ ДИФУЗІЙНОГО ПЕРЕНЕСЕННЯ ТЕПЛОВОЇ ЕНЕРГІЇ

Розглядають закриту термодинамічну систему, яка обмінюється тепловою енергією із довкіллям. При цьому конвективна складова перенесення теплової енергії й ентропії до системи є відсутньою. Оскільки термодинамічна система є твердим тілом, змінюванням її об’єму в першому наближенні можна нехтувати.

Тоді для рівняння

, (1)

де – ентальпія системи, що розглядають; , – відповідно щільність і хімічний потенціал -го компонента, – яке характеризує змінювання параметрів стану системи у просторово-часових координатах для необоротних процесів, мають місце:

, , .

, тому рівняння перенесення (1) набуває вигляду:

, (2)

Використовуючи співвідношення

та вважаючи, що і , одержують

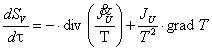. (3)

Згідно до рівняння Умова можна записати

. (4)

Зіставлення співвідношень (3) і (4) дозволяє одержати співвідношення

, .

Виходячи з теореми про виробництво ентропії

, (5)

де – швидкість виробництва ентропії усередині системи за рахунок дисипативних ефектів необоротних процесів перенесення теплової енергії; – питомий тепловий потік дифузійного перенесення теплової енергії, який спричинено дією -ої сили; – -та термодинамічна рушійна сила, – можна записати:

. (6)

Звідки

. (7)

На підставі принципу лінійності потік внутрішньої енергії у системі, що розглядають, визначається співвідношенням

, (8)

де – кінетичний коефіцієнт перенесення внутрішньої енергії, що відображає фізичні властивості системи та її відношення до цього перенесення.

Вводячи позначення , записують

, (9)

Після підставляння співвідношення (9) до рівняння (2) одержують

. (10)

Оскільки ентальпія , то за і рівняння (10) має вигляд:

. (11)

Рівняння (11) є диференційним рівнянням перенесення питомої ентальпії під час взаємодії закритої системи із довкіллям.

Оскільки , де – питома масова теплоємність системи, то за одержують

(12)

або

. (13)

З урахуванням, що можна записати

. (14)

Таким чином, термодинамічний аналіз взаємодії системи із довкіллям, що виконано у роботі, дозволяє одержати диференційне рівняння теплопровідності для декартової системи координат.