Научный руководитель – профессор.т.н. Бейсенби М.А.,

Доктарант – Темиргалиева А. Е.

 

Евразийский национальный университет им. Л.Н.Гумилева

 

Применения детерминированного хаоса для передачи информации

 

Одной из актуальных задач теории управления является методы управления детерминированными хаотическими процессами.

Рассмотрим подробнее некоторые схемы применения хаоса для передачи сообщений [1,4,5] .

 

В данной работе [6,7] передатчик строится как система Лоренца, уравнения которой после масштабирования приводятся к виду:

 

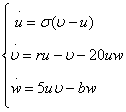(1)

В настоящее время сформировалось новое направление работ, посвященных  выявлению и анализу хаотических процессов,возникающих  в решениях детерминированных уравнений как открытых, так и замкнутых систем. Основным инструментом для выявления хаотических процессов является компьютерное  моделирование уравнений систем и имитация  их параметров [2].

 

Function Synch

Global sigma r b;

Sigma = 16;

R=45,6;

B=4.0;

[T,X]=ode 113 (@dx, [0 200], [10 10 10]);

Plot3(x(: ,1), x(: ,2), x(: ,3)); grid;

 

Function f=dx(t, x)

Global sigma r b;

F=[sigma*(x(2)-x(1));

r*x(1)-x(2)-20*x(1)*x(3);

      5*x(1)*x(2)-b*x(3)];

 

 

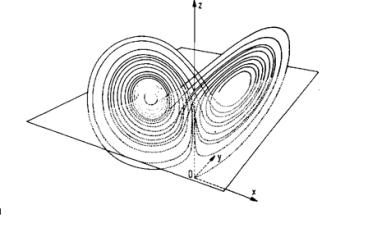
Рис.1  Странный аттрактор Лоренца .

 

В соответствии с (1) построена аналоговая электронная цепь, имеющая параметры= 16,r = 45.6,b = 4.0 (переменные и, , отвечают напряжениям на выходах операционных усилителей).

 

Уравнения приемника взяты в виде:

 

 

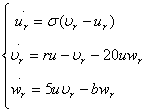
                      (2)

Уравнения (2) похожи на (1), за исключением того, что правая часть (2) зависит не от «своей» переменной состояния ur, а от переменной и, которая таким образом можетрассматриваться как поступающий на приемник выходной сигнал передатчика.

Обозначимпеременныесостоянияпередатчика и приемника в виде векторов , . Определения динамической ошибки.

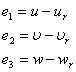
Предполагая, что коэффициенты передатчика и приемника являются идентичными,вычислим динамическую ошибку

 

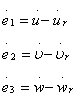
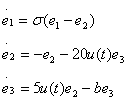
Динамическая ошибкаглобально асимптотически устойчивов начале координатпри условии, что> 0. Этот результатвытекает изтрехмернойфункцией Ляпунова, котораяопределяется таким образом

 

 

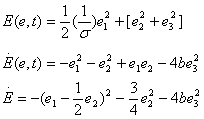
Методом функций Ляпунова в работах [6,7] показано, что системы (1) и (2) синхронизируются, т. е. невязка между их соответствующими переменными состояния асимптотически стре­мится к нулю.

Другими словами, (2) является асимптотическим наблюдателем для (1). Для передачи двоичного сигнала коэффициентb передатчика (1) изменялся, принимая значе­ниеb = 4.4, соответствующее двоичной «единице», тогда как и сходное значениеb = 4.0 означало двоичный «ноль». При изменении величиныbв (1) доb = 4.4 в системе (2) резко возрастает уровень сигнала рассогласованияe =u — ur(так как параметрb наблюдате­ля (2) отличается от значенияb в системе (1)). Усреднением e2(t) определялось, какой из сигналов был передан.

В работе [4,5,7,8] продемонстрирована и возможность применения хаоса для защиты ин­формации. Предложенный там подход известен под названием «хаотического маскирова­ния» (chaoticmasking) и состоит в том, что в передатчике к информационному (полезно­му) сигналу добавляется хаотический, а в приемнике происходит восстановление полезного сигнала из смеси.Для выделения полезного сигнала использовано свойство робастности процесса синхронизации систем (2), (1). Система (2) может, тем самым, рас­сматриваться как фильтр, настроенным, нестрого говоря, в резонанс к хаотическому ге­нератору (1). Поскольку полезный сигнал m(t) имеет принципиально другую форму, чем хаотический, его можно восстановить, подавая на вход приемника (2) смешанный сигнал s(t) = m(t) + u(t), а затем на выходе приемника восстановить по оценкеur(t) переменной u(t) по формулеm(t) = s(t) —ur (t) [5,7,8].

Процесс восстановления приемником передаваемого сообщения на основе синхрониза­ции имеет много общего с известным в теории управления оцениванием состояния объекта с помощью наблюдающего устройства (которое для данных задач реализуется в приемнике).

 

 

 

 

 

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

 

1.     Андриевский Б.Р., Фрадков А.Л. Управление хаосом. Методы и приложения. Часть 1, Методы // Ли Г. 2003. 5. С. 3-45.

2.     Андриевский Б,Р., Фрадков А,Л, Элементы математического моделирования в про­граммных средах MATLAB 5 и Scilab (учебное пособие). СПб.: Наука, 2001, 286 с.

3.        Дмитриев А. С., Панас А.И., Старков С. О. Динамический хаос как парадигма совре­менных систем связи // Зарубежная радиоэлектроника. Успехи современной радио­электроники, 1997, № 10, С, 4-26,

4.        Дмитриев А. С., Кузьм,ин Л.В. Передача информации с использованием синхронного хаотического отклика при наличии фильтрации в канале связи // Письма в ЖТФ, 1999. 25. 16. С 71-77.

5.        Короновский А.А. Москаленко О.И., Храмов А.Е. О применении хаотической синхронизации для скрытой передачи информации. Том 179, №12.

6.        Cuomo K.M., Oppenheim A.V., Strogatz S.H. Synchronization of Lorenz-based chaotic circuits with application to communications // IEEE Trans. Circ. Svst. - II. 1993. 40. 10. P. 626-633.

7.        Cuomo K.M., Oppenheim A.V. Circuit implementation of synchronized chaos with applications to communications // Phvs. Eew. Lett. 1993. 71. 1. P. 65-68

8.        Complexity, chaos, and biological evolution /Eds E. Mosekilde, L. Mosekilde //NATO ASI Series, Ser. B: Physics. New York; London: Plenum Press, 1991. Vol. 270.