Д.т.н. Догода П.А., д.т.н. Степанов А.В.,

ст. пр. Степанова Е.И.

Южный филиал Национального университета биоресурсов и природопользования Украины «Крымский агротехнологический университет», Авт. Респ. Крым, Украина

ПРОЕКТИРОВАНИЕ ПЕРЕХОДНОГО УЗЛА МЕЖДУ ТРАНСПОРТЕРАМИ АГРЕГАТА ДЛЯ УБОРКИ ОВОЩЕЙ НА ОСНОВЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ВЯЗКОУПРУГОГО ВЗАИМОДЕЙСТВИЯ

Проектирование различного рода переходных узлов между транспортирующими механизмами сельскохозяйственных агрегатов представляет собой довольно затруднительную задачу как с точки зрения математического моделирования процессов перемещения упруго-пластичных тел, так и с точки зрения получения точных аналитических или численных (приближенных) с приемлемой точностью решений. Как правило, исследования в этом направлении осуществляются в плане получения эмпирических зависимостей, основанных на опытных данных.

В настоящее время, в связи с освоением энергосберегающих технологий в сельскохозяйственном производстве, весьма актуальна разработка новых конструкций агрегатов для уборки и послеуборочной доработки продукции, в частности, в растениеводстве (овощеводстве). Очевидно, что в этом плане, оптимальное сочетание ручного и механизированного труда даст возможность получать качественную продукцию (без значительных потерь) в достаточных объемах, при снижении ее себестоимости. Например, в комплексе машин по уборке томатов, сконструированы и применяются в производстве такие агрегаты как транспортер овощной конвейерный ТОК-18 («РОСТА», Украина, Мелитополь), платформа для уборки овощей ПУО-1А и ПУО-2 (ПООО «Техмаш», Беларусь, Лида), АУО-14 (НПО «Наука», Украина, Симферополь).

Основные преимущества агрегата АУО-14: легкость конструкции, возможность применения в многоразовой уборке продукции по мере ее созревания и, по сравнению с аналогами ТОК-18 и ПУО-2, более высокий коэффициент механизации труда сборщиков продукции. Экспериментальный образец показал, что наиболее проблематичным элементом конструкции является переходный узел между боковыми транспортерами и центральной частью (рис. 1). Очевидно, что для решения этой конструктивной задачи, в этой части агрегата следует поместить спускное устройство в виде желоба, по которому плоды могли бы под действием силы тяжести перемещаться и попадать на подъемник центральной части. Поверхность такого устройства должна иметь криволинейную направляющую, так что бы при упругом ударе плода и дальнейшем его перемещении, обеспечивалось бы выполнение условия «минимум времени контакта». Таким образом, такая кривая находится в классе брахистохрон [1], а именно среди гипоциклоид.

ОСНОВНОЙ РЕЗУЛЬТАТ РАБОТЫ

По определению – гипоциклоида – это плоская кривая, описываемая точкой окружности, катящейся по другой окружности и имеющей с ней внутреннее касание.

Гипоциклоида в параметрической форме имеет вид:

Рис. 2. Гипоциклоида	Рис. 3. Отражатель в форме гипоциклоиды (кривая )

где радиус катящейся окружности, радиус неподвижной окружности, угол, стягиваемый дугой между точками касания окружностей. Величина модуля определяет вид кривой. При кривая состоит из непересекающихся частей (рис. 2).

Конструкция отражателя в форме гипоциклоиды приведена на рис. 4.

Для рис. 4. , , фиксировано и равно . Находим далее кинетическую энергию в момент удара в некоторой фиксированной точке . При фиксированном , находим значение параметра из уравнения:

Получено квадратное уравнение относительно с дискриминантом и решением: .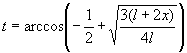

Таким образом:

Отсюда, кинетическая энергия в точке :

,

где скорость боковых транспортерных лент. Составляющие скорости плода в точке (см. рис. 3.):

Откуда:

Кинетическая энергия в точке :

Гипоциклоида относится к так называемым циклоидальным кривым, которые в свою очередь относятся к кривым скорейшего спуска – брахистохронам. Если такая кривая параметрически описывается соотношениями:

то

.

Это условие обеспечивает минимальный по времени контакт плода с поверхностью отражателя.

Очевидно, что параметры желоба могут быть определены из решения задачи контактного взаимодействия вязкоупругого тела (плод) и поверхности.

В [2] Г. Герц предполагал, что упругая сила контактного взаимодействия тел при ударе зависит от деформации так же, как и в случае статического нагружения. Было показано, что если тело и препятствие в окрестности соприкосновения имеют сферическую поверхность и их деформации малы по сравнению с их радиусами, то с увеличением пятна контакта с ростом деформации сила упругого взаимодействия равна , где константа, значение которой определяется радиусами этих сферических поверхностей и материалом контактирующих тел. В [2] показано, что уравнение движения тела при этом имеет интеграл энергии, который интегрируется в квадратурах.

Модель Г. Герца была обобщена К. Хантом и Ф. Кроссли [3], введением в рассмотрение силы сопротивления:

, (1)

где коэффициент упругости, постоянная сопротивления, постоянная, которая определяется формой поверхности тела и препятствия в окрестности точки контакта, перемещение тела (деформация), причем . Для сферической поверхности тел .

Обозначая: скорость тела до удара и скорость после удара, можно получить коэффициент восстановления при ударе, как отношение модулей указанных скоростей:

. (2)

При малых скоростях соударения, коэффициент восстановления линейным образом зависит от и .

Модель (1) может быть обобщена:

, (3)

где упругая сила взаимодействия при ударе такая, что монотонно возрастающая функция при и . Таким образом, уравнение движения тела примет вид:

, (4)

где масса тела. Тривиальное решение уравнения (4): .

Обозначим потенциальную энергию упругой деформации. Тогда:

. (5)

Используя: , после подстановки в уравнение (4), разделения переменных и интегрирования, получим:

Откуда:

. (6)

Уравнение (6) – трансцендентное и может быть решено относительно с помощью специальной функции Ламберта [3]. , где: монотонно убывающая функция при ; для фазы восстановления (основная ветвь функции ) и для фазы деформации (вторая вещественная ветвь функции – пунктирная линия) (рис. 4). График функции может быть также легко построен. При этом максимальное перемещение тела при ударе определяется как решение уравнения: .

Таким образом, зная физико-механические и геометрические параметры соударяющихся тел, можно определить максимальное перемещение одного относительно другого. Возвращаясь к задаче проектирования поверхности ската в конструкции агрегата, важно, зная параметры перемещаемых плодов, из условия минимального перемещения (при отскоке), подобрать форму и материал поверхности отражателя так, что бы . Из этих соображений, форма отражателя имеет вид поверхности с направляющей в виде гипоциклоиды с параметром (рис. 5) и образующими в виде эллипсов с возрастающим к единице эксцентриситетом к верхней части поверхности отражателя (рис. 6). По известным размерам, поверхность отражателя может быть задана таблицей значений, как функция двух переменных.

	а). б).
Рис. 5. Направляющая в виде гипоциклоиды	Рис. 6. Поверхность отражателя: а). выполненная в MS Excell, б). модель.

ВЫВОДЫ

Проектирование переходных узлов между рабочими органами сельскохозяйственных агрегатов для уборки и послеуборочной доработки овощей является одной из актуальных задач, которая связана с внедрением энергосберегающих технологий. Математическое моделирование процессов взаимодействия продукции с элементами агрегата относится к классу задач вязкоупругого взаимодействия тел с различными физико-механическими и геометрическими параметрами. Учет режимов вязкоупругих взаимодействий позволит осуществлять модификации конструкций с целью снижения потерь.

ЛИТЕРАТУРА

1. Математическая энциклопедия / И.М. Виноградов (глав.ред.)[и др.], Т.1. – М.: Советская Энциклопедия. – 1977. – 1152 с.

2. Hertz H. Über die Berührung fester elastischer Körper // Journal reine und angewandte Mathematik. – 1882. – B. 92. – S. 156-171.

3. Hunt K.H., Crossley F.R.E. Coefficient of restitution interpreted as damping in vibroimpact // ASME Journal of applied mechanics. – 1975. – № 6. – P. 440-445.

4. Corless R.M., Gonnet G.H., Hare D.E.G., Knuth D.E. On the Lambert W function // Advances in computational mathematics. – 1996. – V. 5. – P. 329-359.

Summary. Planning of different sort of transitional knots between the transporting mechanisms of agricultural asms is an enough difficult task both from the point of view of mathematical design of processes of moving of resiliently-plastic bodies and from the point of view of receipt of exact analytical or numeral (close) with acceptable exactness decisions. As a rule, researches in this direction are carried out in the plan of receipt of empiric dependences, based on the experienced data.

Анотація. Проектування різного роду перехідних вузлів між транспортуючими механізмами сільськогосподарських агрегатів є досить скрутним завданням як з точки зору математичного моделювання процесів переміщення пружно-пластичних тіл, так і з точки зору отримання точних аналітичних або чисельних (наближених) з прийнятною точністю рішень. Як правило, дослідження в цьому напрямі здійснюються в плані отримання емпіричних залежностей заснованих на досвідчених даних.