Костарев Д.Д., Рябушкин С.А.

Тольяттинский государственный университет,

специальность «Прикладная информатика», 4 курс

Научный руководитель: Гущина О.М.,

к.п.н., доцент кафедры «Информатика и ВТ»

Прогнозирование социально-экономических процессов с применением уравнения регрессии

Прогноз всегда был важен для общества. Будучи многогранным, прогноз не привязан ни к одной стороне человеческой деятельности или различным природным явлениям. Все знают про прогноз погоды, но это далеко не единственная, хоть и наглядная, возможность получения прогноза и выгоды от него. В свою очередь, разработку прогноза принято называть прогнозированием, которое применимо для многих явлений и процессов. Существует несколько видов процессов: политические, экономические, социально-экономические и т.д. Прогнозирование наиболее часто применяется в социально-экономических процессах.

Получение прогноза – достаточно трудоемкий и требовательный процесс, который занимает много времени. Обычно для прогнозирования используются следующие методы: экстраполяция известных данных, моделирование некоторых ситуаций или вариативная оценка, полученная на основе экспертных данных. Для их решения можно применять стандартные математические средства и средства компьютерных технологий, такие как: построение прогнозных рядов и использование стандартных функций в MS Excel. Но, как правило, данные методы занимают много времени для вычислений и требуют специальных знаний. Для ускорения процесса получения прогноза можно использовать различные автоматизированные системы, которые обычно содержат несколько определенных методов, необходимых для получения того или иного варианта прогнозного результата. В качестве средств создания подобных систем используют различные языки программирования, с помощью которых можно описать поведение объекта в будущем, основываясь на моделировании социально-экономических процессов с помощью уравнения регрессии.

Для начала необходимо понять, что же такое социально-экономический процесс. Это явление представляет собой изменения в обществе, которые отражаются на его благосостоянии, политической и экономической стабильности, условиях безопасности и прочем. Главная особенность социально-экономических процессов – тесная привязка к деятельности предприятий, крупных национально-государственных систем и регионов, которая определяет масштабы, уровень, темпы и цели происходящего в русле этих, постоянно меняющихся, объектов. Как и многие другие процессы, социально-экономические можно прогнозировать; для этого существуют три основных класса моделей: модели временных рядов, системы эконометрических уравнений и регрессионные модели. Наиболее точным является последний класс, потому что в отличие от других средняя ошибка (доверительный интервал) прогноза рассчитывается с достаточно большой надежностью.

Рассмотрим наиболее значимые понятия данного класса: регрессия и уравнение регрессии. Важнейшим из них является понятие регрессии – это зависимость среднего значения какой-либо величины от некоторой другой величины или нескольких величин. В отличие от чисто функциональной зависимости y = f(x), когда каждому значению переменной x соответствует одно определенное значение y , при регрессивной зависимости одному значению x могут соответствовать несколько значений y (в зависимости от случая). Из этого определения следует понятие уравнения регрессии, которое представляет собой уравнение y = u(x), в котором x играет роль "независимой" переменной, а соответствующий график - линией регрессии величины Y по X. Точность, с которой уравнение регрессии Y по X отражает изменение Y в среднем при изменении x, измеряется мерой разброса величины Y вычисленной для каждого значения X=x.

Рассмотрим процесс прогнозирования величины расходов в зависимости от доходов. Кроме того определим основные задачи:

1) выделить объект, который содержит необходимые данные для решения задачи: статистические данные среднедушевых месячных доходов и расходов за 2010 год конкретного региона;

2) построить однофакторную модель регрессии зависимости расходов от доходов;

3) проверить значимость параметров модели регрессии;

4) построить доверительный интервал для полученной модели регрессии;

5) оценить расходы, если доход составляет величину прожиточного минимума.

Основным средством решения обозначенных задач будет использование автоматизированной системы, разработанной средствами языка программирования Delphi (рис. 1).

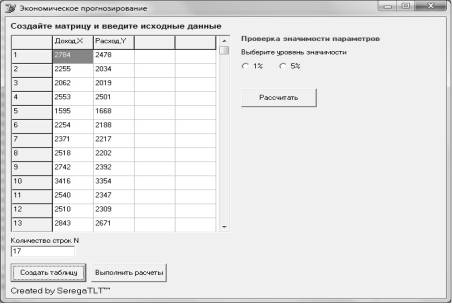
Рис. 1. Табличное представление данных доходов и расходов

Для решения обозначенной задачи определим зависимость расходов от доходов. Обозначим – постоянная величина, параметр β – коэффициент регрессии, величина которого показывает среднее изменение результата с изменением фактора на единицу.

	(1)
	(2)

В итоге получаем модель зависимости расходов от дохода, которая показывает, что при увеличении дохода на определенную величину, расходы увеличатся в среднем на величину β:

(3)

Следующим шагом является проверка значимости параметров модели регрессии (рис. 2). Для этого необходимо рассчитать значение t-критерия () по формулам:

	(4)
	(5)
где	(6)

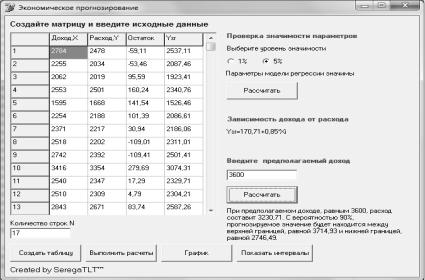
Рис. 2. Проверка значимости параметров модели регрессии

Полученное значение t-критерия () (5) сравним с табличным значением t-критерия Стьюдента (). Если || > , то коэффициент β значим, что позволяет использовать данные факторы для создания прогнозной модели.

Завершительным этапом в построении модели регрессии является расчет доверительного интервала (7) для прогнозирования индивидуальных значений y_i (рис. 3).

(7)

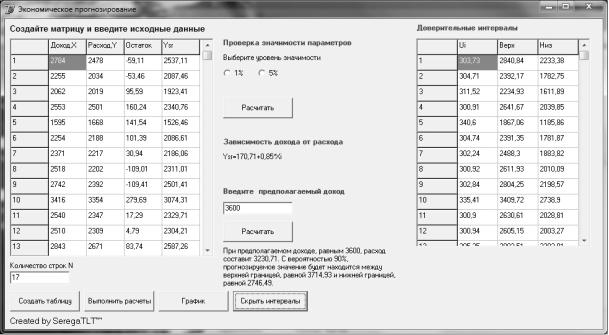
Рис. 3. Данные доверительного интервала

Результатом проделанных действий является сформированная таблица, содержащая статистические данные среднедушевых месячных доходов и расходов за 2010 год конкретного региона и возможного отклонения фактического значения от значения, полученного при расчетах. На основании этих данных строится график зависимости расходов от дохода (рис.4), позволяющий наглядно просчитать требуемые показатели.

Рис. 4. График зависимости расходов от доходов

Данный пример наглядно демонстрирует преимущества использования автоматизированных систем в получении точечного и интервального прогноза развития социально-экономических процессов при помощи уравнения регрессии.