Філатова Г.М., Чернишева С.В.

Автомобільно-дорожній інститут

державного вищого навчального закладу

«Донецький національний технічний університет»

Побудова математичної моделі поведінки об’єктів і об’єктних відносин системи «Матеріальне стимулювання праці»

Під системою оплати праці розуміється спосіб обчислення розмірів винагороди, що підлягає виплаті працівникам підприємства згідно із здійсненими ними витратами праці або за результатами роботи.

Система оплати праці регулюється Кодексом законів про працю (КЗпП) та системою угод, що укладаються на відповідних рівнях: колективний договір та індивідуальний трудовий договір.

Економіко-математичний аналіз вирішення оптимізаційних завдань — полягає перш за все у виявленні умов, при яких отримане рішення задачі стійке, тобто знайдений план залишається оптимальним при порівняно невеликих змінах початкових і інших зовнішніх умов. Для цього прораховується і порівнюється ряд більш менш схожих варіантів завдання.

Об’єктом дослідження даної статті є система матеріального стимулювання праці. Предметом дослідження є модель системи матеріального стимулювання праці. Метою написання статті є побудова фрагментів моделі системи матеріального стимулювання праці системи.

Розглянемо питання математичного моделювання поведінки об'єкту «МСП» для подальшого визначення кількісних характеристик елементів потоку управління.

В рамках лінійної моделі монетарної системи матеріального стимулювання праці поставимо наступне завдання:

Є n робіт з вагами значущості k₁, k₂ ., k_n і n постачальників об'єктивних відомостей про якість виконання робіт а₁, а₂ ., а_n m виконавцями b₁, b₁, b₂., b_m з ефективностямі роботи е₁,е₂.,е_m. Потрібно так розподілити фонд стимулювання S, щоб сумарна ефективність була максимальною.

Вважатимемо, що число виконавців робіт m не більше, ніж число робіт n. Випадок же, коли m більше n вважатимемо виродженими. У роботі розглядається випадок m = n, тобто число виконавців рівне числу робіт.

Крім того, коефіцієнти значущості робіт вважаються рівними одиниці k_i = 1, що, на нашу думку, визначає лінійність завдання, а випадок коли k_i ≠ 1 відповідає нелінійній моделі. Введемо наступні позначення:

- Z_i розмір стимулу i-го виконавця;

- e_i ефективність i-го виконавця;

- k_j - значущість j-той роботи;

- z_ji - i -тая частина стимулу виконання j - тієї роботи;

- n_j - кількість частин стимулу j - тієї роботи.

Щодо ефективності виконавця керуватимемося наступними міркуваннями.

У виконавця, що вперше виконує роботу, ефективність приймається рівній одиниці, оскільки, будучи призначеним на виконання роботи, відносно його, отже, було зроблено (об'єктивно чи ні) припущення про його потенційну ефективність.

У працюючого виконавця ефективність залишатиметься рівній одиниці при стовідсотковому виконанні роботи або підвищуватися за рахунок тієї частини фонду стимулювання, яка буде утворена в процесі виробництва на основі підвищення ефективності виконавця.

Ефективність виконавця зменшується у разі не стовідсоткового виконання роботи на стільки відсотків, на скільки відсотків не виконана робота.

Під періодом оцінювання розумітимемо проміжок часу від початку виконання праці до моменту нарахування заробленої плати.

Викладені міркування дозволяють отримати аналітичний вираз для визначення величини стимулу i-того виконавця .

,

(1)

де Z_i розмір стимулу i-го виконавця;

e_i ефективність i-го виконавця;

k_j - значущість j-той роботи;

z_ji - i -тая частина стимулу виконання j - тієї роботи;

n_j - кількість частин стимулу j - тієї роботи.

Отриманий аналітичний вираз вважатимемо математичною моделлю поведінки об'єкту «МСП», що дозволяє визначити кількісну характеристику властивості об'єкту «МСП» як числового виразу елементу потоку управління, - «розрахувати МСП».

Таким чином, в процесі написання роботи отримана математична залежність, що дозволяє знайти кількісні характеристики елементів потоку управління системи, з одного боку, і, з іншого боку, модель поведінки об'єкту системи.

Література:

1. Власов М.П. Моделирование экономических процессов / М.П. Власов, Т.Д. Шимко. – Ростов-на-Дону: Феникс, 2005. – 409 с.

2. Катренко А.В. Системний аналіз об’єктів та процесів комп’ютеризації: Навч. посіб. / А.В.Катренко – Львів: «Новий світ – 2000», 2003. – 424 с.

3. Федосеев В.В. Экономико-математические модели и прогнозирование рынка труда: Учеб. пособие. / В.В.Федосеев – М.: Вузовский сборник, 2005. – 144 с.
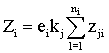