Математика/3.Теория вероятности и математическая статистика

Бесарабов В.О.

Донецький Національний Університет Економікі і Торгівлі імені Михайла Туган-Барановського

Індивідуальні індекси в статистиці

Індекс (index) у статистиці – узагальнюючий відносний показник, який характеризує співвідношення в часі чи просторі соціально-економічних явищ і процесів. За допомогою індексів вивчають зміну обсягу виробництва різнорідної продукції, цін на різні види товарів, продуктивності праці у галузях матеріального виробництва. Їх також використовують і для визначення ступеня впливу окремих факторів на зміну окремого явища.

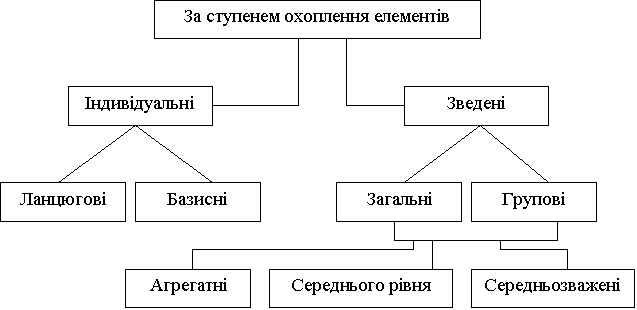
У статистиці розрізняють кілька видів індексів. В основу класифікації покладено два різні критерії: за ступенем охоплення елементів; за способом побудови. За ступенем охоплення елементів розрізняють індекси: індивідуальні; зведені. У свою чергу індивідуальні бувають: базисні; ланцюгові. Зведені індекси поділяються на: загальні; групові. За способом побудови зведені індекси поділяються на: агрегатні; середньозважені.

Цю класифікацію можна показати схематично

Індивідуальні індекси служать для характеристики зміни окремих елементів складного явища (наприклад, зміна обсягу випуску телевізорів певної марки, зростання або падіння цін на акції в будь-якому акціонерному товаристві і т.д.). Індивідуальні індекси позначають буквою і та супроводжують підрядковим значком індексуючого показника, тобто показника, співвідношення рівнів якого характеризує індекс. Індекс цін позначають символом і_р, індекс фізичного обсягу і_g тощо. Показники за період, з яким проводиться порівняння /базисний період/, мають підрядкову цифру «0», а показники за період, що порівнюється /звітний чи поточний/ «1» (наприклад: ціна базисного періоду – р_о; обсяг виробництва – q₀; собівартість одиниці продукції - z_o; продуктивність праці - w_o; трудомісткість -t_o; товарообіг - p_o*q_o; та відповідно поточний період, буде характеризуватися наступними показчиками: p₁, q₁, z₁, w₁, t₁, p₁*q₁) Якщо зміна явища вивчається більше, ніж за два періоди, то кожен з показників цих періодів позначається відповідно цифрами «2», «3» і т.д. У цьому випадку “базисним” може служити як показник початкового періоду, так і будь-який інший показник, що передує звітному показнику. Ім'я «звітного» показника надається по черзі всім наступним показникам з номерами «1», «2», «3», …, і далі..Основні економічні індивідуальні індекси з формулами:

Назва	Розрахункова формула
1. Індекс ціни	ip = p1/p0
2. Індекс кількості продажу (виробництва) продукції	iq = q1/q0
3. Індекс товарообігу	IQ = Q1/Q2
4. Індекс собівартості продукції	iz = z1/z0
5. Індекс продуктивності праці	iv = v1/v0 iw = w1/w0 it = t1/t0

Індивідуальний індекс дуже простий у своєму розрахунку і тут ніяких методологічних труднощів не виникає. Однак, і при розрахунку індивідуального індексу необхідно враховувати сутність розглянутого ознаки (показника, явища). Наприклад, рівень продуктивності праці може оцінюватися з використанням двох взаємопов'язаних показників - вироблення (обсягу виробленої продукції в одиницю часу) або трудомістко (витратами праці на виробництво однієї одиниці продукції). Між цими показниками існує зворотна залежність. Підвищення продуктивності праці виражається або збільшенням виробітку або зниженням трудомісткості. У першому випадку використовується відомий індексний вираз, а в другому випадку індивідуальний індекс продуктивності праці визначається як рівень трудомісткості базисного періоду і рівнем трудомісткості звітного періоду. Іншою особливістю індивідуальних індексів є те, що вони характеризують зміну в часі (або співвідношення в зміні) одиничних простих показників.
Однак набагато частіше доводиться за допомогою індексів характеризувати зміни зведених показників, складних явищ. Строго кажучи, такого роду зведені відносні показники, що характеризують зміну складного явища в цілому, являють собою власне індекси, до побудови яких і відноситься теорія індексів.

Література:

1. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. -М.: Инфра-М, 1999.

2. Малыхин В.И. Математическое моделирование экономики. -М: УРАО, 1998.

3. Вероятность и математическая статистика. Энциклопедия / Гл. ред. Ю. В. Прохоров. — М.: Изд-во «Большая Российская Энциклопедия», 1999.

4. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика: Учебник / Под ред. В.А. Колемаева. — М.: ИНФРА-М, 1997. - 302 с. - (Серия «Высшее образование»).