Математика/ 5. Математическое моделирование

к.ф.-м.н. Искакова А.С., Мухамбетов М.К.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Об одном методе определения несмещенных оценок вероятностей процессов энергетических характеристик радиолинии ИСЗ Meteosat

Одной из характерных особенностей поставленных перед Астанинским филиалом АО "НЦКИТ" центра космического мониторинга является регулярный прием и запись входного потока данных дистанционного зондирования земли с космических аппаратов IRS-1C, IRS-1D, IRS-P6, RADARSAT, AQUA находящихся в зоне радиовидимости.

Телеметрическая информация передается с борта спутника на частоте 1675.928 МГц, вид модуляции КИМ-ФМ2/180-ЧМ. Для передачи телеметрии используется направленная антенна S-диапазона частот с высоким коэффициентом усиления, а на этапе вывода ИСЗ на орбиту — ненаправленная антенна S-дпапазона частот. Командная информация принимается на частоте 2098.0 МГц с помощью направленной антенны S-диапазона с высоким коэффициентом усиления.

На энергетические характеристики радиолинии передачи данных в режиме HR с ИСЗ Meteosat серии МОР /22/ влияют ЭИИМ, потери на распространение, потери на наведение антенны (), КНД приемной антенны с диаметром зеркала 4 м, потери в фидерных линиях, потери на отражение, принимаемая мощность ), модуляционные потери, эффективный принимаемый сигнал ), шумовая температура антенны для угла места 30°, шумовая температура РПУ, шумовая температура системы ), спектральная плотность шума ), скорость передачи информации 166 кбит/с , общая мощность шума ), отношение с/ш (9-15), потери демодулятора, эффективное отношение с/ш ), требуемое отношение с/ш для вероятности ошибки, запас мощности для вероятности ошибки, добротность системы () ). Иными словами на искажение влияют 23 фактора, то есть .

Рассмотрим вероятностную модель процессов энергетических характеристик радиолинии ИСЗ Meteosat. В работе [1] приведена вероятностно-статистическая вероятности оправдываемости метеорологического прогноза.

Допустим, что истинное изображение представимо в виде матрицы , на которые наложили искажение , состоящее их четырех факторов (матриц) искажений, принимающие значения из множества .

Очевидно, что факторы (матрицы) искажения являются реализациями случайных матриц , которые проявляются с соответствующими вероятностями , причем 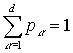. Обозначим через число разбиений матрицы на матрицы . Иными словами, представляет количество решений следующей системы уравнений

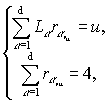
где для каждого элементы вектора , элементы которого принимают значения от 0 до 23.

Предложение. Вероятность того, что искажение значение определяется по формуле

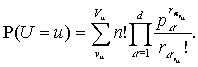(1)

На практике, как правило, элементы вектора 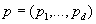не известны. Также не известны матрицы 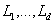. Следовательно, формула (1) не находит фактического применения.

Допустим, что имеются снимки в количестве определенной местности с искажениями . Иначе говоря, ряд фактических данных можно трактовать как реализацию выборки объема , элементы которой подчиняются распределению (1).

Обозначим через вектор , который определяет – ое решение системы уравнения

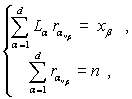(2)

, где – число разбиений матрицы на матрицы . Используя решения системы уравнений (2), матрицыи фактические данные , определим для каждого число разбиений матрицы на и векторы . Пусть, при , где 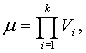вектор представляет решение, основанное на наблюдении, которое имеет следующий вид .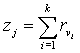

Теорема 1. Элементы множества являются несмещенными оценками для вероятности распределения (1), которые при определяются как

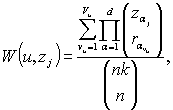(3)

где –число разбиений матрицы на части ; для каждого разбиения определяют возможное количество матрицами ; и , при .

Итак, имеем множество несмещенных оценок вероятности проявлений искажений. Наиболее подходящая несмещенная оценка для вероятности оправдываемости метеорологического прогноза распределения (1) определяется из всего множества полученных несмещенных оценок , согласно определениям.

Определение 1. Решение , основанное на наблюдении, является наиболее подходящим из множества если

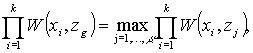(4)

где при элементы множества являются несмещенными оценками для вероятности распределения (1), определенными в (3).

Определение 2. Несмещенная оценка для вероятности распределения (1) является наиболее подходящей из всего множества несмещенных оценок , определяемых в (4), если – наиболее подходящее решение, основанное на наблюдении.

Теорема 2. Наиболее подходящая несмещенная оценка для вероятности модели (1) является состоятельной, асимптотически нормальной и асимптотически эффективной.

Литература:

1. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84.

2. И.Лисов. Искусственные спутники Земли. // Новости космонавтики, № 01, 1996.