Математика/ 5. Математическое моделирование

Амантай А.А., к.ф.-м.н. Искакова А.С.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Об одном методе моделирования прогнозов финансовых активов

Одними из задач поставленных перед владельцами финансовых активов является составление прогноза доходов.

По консолидированной финансовой отчетности владельцев финансовых активов имеем статистические данные доходов за последние k лет

y₁=f(x₁), y₂=f(x₂), …, y_k=f(x_k).

1. Построение аналитической зависимости доходов финансовых активов. Одними из задач поставленных перед владельцами финансовых активов является составление прогноза доходов.

По консолидированной финансовой отчетности владельцев финансовых активов имеем статистические данные доходов за последние k лет

y₁=f(x₁), y₂=f(x₂), …, y_k=f(x_k).

Нас интересует, как выглядит функциональная зависимость между x_i и y_i, где i определяет год отчетности.

Пусть y – функция одной переменной с двумя параметрами a и b. Согласно [1], в качестве набора выбора функций, из которых будем иметь эмпирическую зависимость, рассмотрим: линейную функцию ; показательную функцию ; дробно-рациональную функцию ; логарифмическую функцию ; степенную функцию ; гиперболическую функцию ; дробно-рациональную .

Для наилучшего выбора вида аналитической зависимости y=f(x,a,b), соответствующий построенному графику, построим следующие промежуточные вычисления. На заданном отрезке изменения независимой переменной выберем точки, достаточно надежные и по возможности, далеко отстоящие друг от друга. Будем считать, что это x₁ и x₂. Вычислим среднее арифметическое , среднее геометрическое и среднее гармоническое 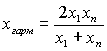. По вычисленным значениям независимой переменной найдем из построенного графика соответствующие значения переменной , , для пока еще неизвестной аналитической зависимости y=f(x,a,b). Вычислим среднее арифметическое крайних значений , среднее геометрическое и среднее гармоническое . Оценим следующие погрешности: , , , , , , . Пусть ε=min{ ε₁, ε₂, …, ε₇}. Тогда имеем следующее:

1. Если ε=ε₁, то в качестве аналитической зависимости для данного графика хорошим приближением служит линейная функция .

2. Если ε=ε₂, то в качестве аналитической зависимости для данного графика хорошим приближением служит показательная функция .

3. Если ε=ε₃, то в качестве аналитической зависимости для данного графика хорошим приближением служит дробно-рациональная функция .

4. Если ε=ε₄, то в качестве аналитической зависимости для данного графика хорошим приближением служит логарифмическая функция .

5. Если ε=ε₅, то в качестве аналитической зависимости для данного графика хорошим приближением служит степенная функция .

6. Если ε=ε₆, то в качестве аналитической зависимости для данного графика хорошим приближением служит гиперболическая функция .

7. Если ε=ε₇, то в качестве аналитической зависимости для данного графика хорошим приближением служит дробно-рациональная функция .

Для уточнения коэффициентов a и b выбранной аналитической зависимости y=f(x,a,b) можно воспользоваться методом средних или методом наименьших квадратов.

Пример 1. Подберем эмпирическую зависимость для функции дохода грузовых перевозок АО «Национальной компании Казакстан темiр жолы», по имеющимся следующим статистическим данным: 2005г. – 175627754; 2006 г. – 209511577; 2007 г. – 243114528; 2008 г. – 295646874.

В данном случае имеем статистические данные за последние 4 года. Проведем вычисления: , и ; , , ; =2356714, =227867936,44 и =220354728,95. Из проведенных сравнений получаем, что ε=ε₂, следовательно, в качестве аналитической зависимости дохода от грузовых перевозок следует выбрать показательную функцию . С использованием метода средних были определены коэффициенты a и b. Таким образом, получили аналитическое выражение функции дохода от грузовых перевозок .

2. Построение критериев ожидаемых прогнозов финансовых активов страхового портфеля страховой компании «АТФ Полис».

В предыдущем пункте выводились эмпирические функции доходов (операционных расходов). Разумеется, что значения от эмпирических формул, в основном, в какой-то степени расходятся с фактическими данными.

В связи с этим, маловероятно построение идеального прогноза финансового актива. Отметим, что значения эмпирической функции дохода представляют собой средний ожидаемый доход или эффективность операции. Тогда риском r_i (i- конечное натуральное число) операции является модуль разности ожидаемого дохода q_i и значения эмпирической функции y_i, то есть r_i =|q_i -y_i|.

По правилу Вальда или по правилу крайнего пессимизма за рекомендуемый прогноз дохода следует принять прогноз со значением

.

Так, например, при рассмотрении прогноза дохода от грузовых перевозок имеем r₁ =9485174, r₂ =6049609, r₃ =6049609, r₄ =9485174 и . Значит, правило Вальда рекомендует принять прогноз дохода в виде .

Аналогично правилу Вальда можно определить крайние оптимистические прогнозы как

.

Очевидно, что значение прогноза дохода (операционного расхода), принимающие значения больше крайних пессимистических и меньше крайних оптимистических прогнозов, удовлетворяет следующему условию

или

.

Литература:

1. Малыхин В.И. Финансовая математика. –М.:Юнити, 2003. -237 с.

2. Искакова А.С. Условие существования оценок максимального правдоподобия для параметров одного класса многомерных распределений // Известия МОН РК, НАН РК. 2004 г. №1. – С. 90-95.

3. Искакова А.С. Об определении некоторых оценок одной вероятностной модели // Евразийский математический журнал. -2005, №2.- С. 87-101.