Математика/ 5. Математическое моделирование

к.ф.-м.н. Искакова А.С., Искаков Т.М.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Моделирование оценок максимального правдопадобия одного класса дискретных распределений

Как известно, оценки максимального правдоподобия, при выполнении определенных условий (см. [1, стр. 544]), обладают важными свойствами в теории оценивания. Иными словами, они являются состоятельными, асимптотически нормальными и асимптотически эффективными.

Рассмотрим случай, когда оценки максимального правдоподобия не всегда существуют. Предположим, что урна содержит шары, и каждый шар в урне помечен некоторым значением прямоугольной матрицы , где элементы матрицы l_ai произвольные целые числа из известного конечного множества. Допустим, что число возможных матриц L_a есть d.Пусть элементы вектора p=(p₁, … , p_d) определяют вероятности извлечения из урны шара, помеченного соответственными матрицами L₁, … , L_d, причем .

Производится последовательное извлечение n шаров из урны с возвращением, причем неизвестно, какие именно шары были вынуты из урны. Известно только значение матрицы которая представляет сумму матриц на n вынутых из урны шаров. Для изучения данной ситуации требуется построение распределения вероятности u. Допустим, что V_u представляет число возможных сочетаний r_1vuL₁,…, r_{d vu}L_d,которые в сумме образовали матрицу u, где r_1vu,…, r_{d vu} определяют возможное количество вынутых шаров, которые помечены соответствующими матрицами L₁,…, L_d. Иначе говоря, из работы [2] следует, что V_u есть число разбиений матрицы u на части L₁,…, L_d. Из результатов работ [3-5] следует следующее утверждение. Вероятность, что случайная величина U примет значение матрицы u, есть

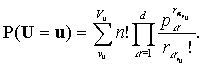(1)

Очевидно, что на практике не известны элементы вектора p=(p₁, …, p_d).

Следовательно формула (1) не находит фактического применения. В связи с этим возникает необходимость определения оценки вероятности (1).

Пусть Х=(X₁, ..., X_k) представляет выборку объема k из распределения (1) и х=(x₁, ..., x_k) есть наблюдавшиеся значения Х, где элементы х_i (i=1, …, k) представляют сумму матриц на n шарах, последовательно вынутых из урны с возвращением. Для каждого i=1, ..., k определим V_i число разбиений х_i на матрицы L₁, … , L_d. Векторы r_1i=(r_11i,…, r_d1i), …, r_Vi=(r_1Vi,…, r_dVi), определяющие эти разбиения.

Найдем оценки максимального правдоподобия для параметров p₁, … , p_d распределения (1). Логарифмическая функция правдоподобия для параметров p₁, … , p_d распределения (1) можно представить в виде

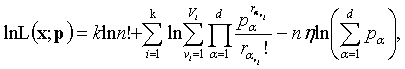
Где 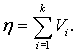Из чего следует, что при любом Δ=1, ¼ , d имеем

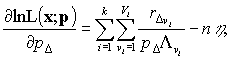(2)

где при i=1, … , k, v_i=1, … , V_i

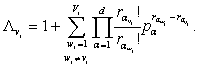(3)

Как известно, оценки максимального правдоподобия 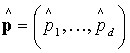для параметров p=(p₁, … , p_d) удовлетворяют следующему при Δ=1, ¼ , d

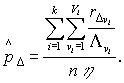(4)

Так как то

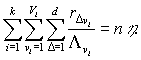(5)

В силу (3) очевидно, что L_vi³1, при i=1, … , k, v_i=1, … , V_i, причем L_vi=1, если V_i=1, иначе L_vi>1. Из чего следует, что

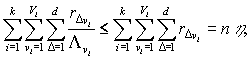
то есть

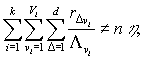
если при каком-нибудь i=1, …, k L_vi>1.

Значит (6) выполняется в случае, если V_i=1 при всех i=1, …, k. Следовательно, построение оценок максимального правдоподобия для параметров распределения представленной модели возможно только в том случае, когда элементы реализации выборки имеют не более одного разбиения на представленные части. Иными словами, если при всех i=1, …, k V_i=1, то L_vi=1, а значит в силу (4) при Δ=1, ¼, d имеем

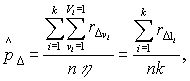
то есть

(6)

Таким образом, верна следующая теорема.

Теорема. Если все элементы реализации выборки х=(x₁, ... , x_k) из распределения (1) имеют не более одного разбиения на представленные части, то существуют оценки максимального правдоподобия для параметров распределения (1), определяемые как

Следствие. Если какой-нибудь элемент реализации выборки х=(x₁, ... , x_k) из распределения (1) имеет более одного разбиения на представленные части, то не существуют оценки максимального правдоподобия для параметров распределения (1).

Таким образом, не всегда возможно построение оценок максимального правдоподобия для параметров распределения (1).

Литература:

1. Крамер Г. Методы математической статистики. – М. 1975. – 648 c.

2. Andrews G.E. The theory of partitions, Encyclopedia of Mathematics and Its Applications (Rota, et.). G.-C. Addison - Wesley, Reading. 1976. Vol.2. 256p

3. Искакова А.С. Об определении некоторых оценок одной вероятностной модели // Евразийский математический журнал.- Астана, 2005.- №2. – С. 87-101.

4. Искакова А.С. Условие существования оценок максимального правдоподобия для параметров одного класса многомерных распределений // Известия МОН РК, НАН РК. Серия физико-математическая.- Алматы: НИЦ “Ғылым”, 2004.- №1. – С. 90-95.

5. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии // Сибирский журнал индустриальной математики.- Новосибирск: Издательство института математики, 2002. – Том V, №1(9).- С. 79-84.