Математика/ 5. Математическое моделирование

Жунусова А.К.

Школа –лицей №1 города Астаны, Казахстан

Об одной модели урновой схемы с шарами

Модели урновых схем с шарами, как отражение существующей реальности, оказываются совершенно необходимыми для описания очень многих явлений и ситуаций, встречающихся в повседневной жизни.

Представим следующую проблему. Наблюдаются суммарные количества потребной электроэнергии, причем совершенно неизвестно, как была эта энергия израсходована (на освещение, на бытовые и технические приборы и т.д.). Требуется определить вероятность, что на предстоящий период времени расход электроэнергии примет некоторое значение u. Другим исключительно актуальным примером применения подобной модели является рекламная индустрия. Аналогичные задачи часто встречаются в метеорологии и в других областях.

1. Определение частности шаров, помеченных числами

Предположим, что урна содержит N шары, и каждый шар в урне помечен одним из возможных чисел l₁, l₂, ..., l_n. Пусть количество шаров в урне с числом l₁ является m₁, с числом l₂ – m₂, и так далее, с числом l_n – m_n. Очевидно, что

Определим значения p₁, … , p_n как

…, .

То есть значения p₁, … , p_n определяют вероятности (или частности) появления шара с соответствующим числом l₁, l₂, ..., l_n. Так как , то

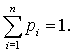(1)

Пример 1. Урна содержит 20 шаров, и каждый шар в урне помечен одним из возможных чисел 5, 7, 11, причем 6 шаров с числом 5, 10 шаров с числом 7 и 4 шара с числом 11. Иными словами, N=20, l₁=5, l₂=7, l₃=11, m₁=6, m₂=10, m₃=4. Как видно, . Вероятность извлечения из урны шара с числом 5 есть вероятность извлечения из урны шара с числом 7 есть вероятность извлечения из урны шара с числом 11 есть

Проверим выполнение формулы (1)

то есть выполнение формулы (1) справедливо.

2. Об извлечении шаров из урны с возвращением.

Рассмотрим случай, когда производится последовательное извлечение k шаров из урны с возвращением. Причем были извлечены r₁ шары с числом l₁ , r₂ шары с числом l₂ , и так далее, r _n шары с числом l_n. Очевидно, что

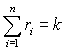
Теорема 1. Количество всевозможных извлечений k шаров из урны с N шарами с возвращением равна .

Доказательство. Количество всевозможных извлечений k шаров из урны с N шарами с возвращением есть число k-перестановок из N элементов (см [1] стр.12), которое определяется, как . Теорема доказана.

Теорема 2. Количество всевозможных извлечений k шаров из урны с возвращением, при которых были извлечены r₁ шары с числом l₁ , r₂ шары с числом l₂ , и так далее, r _n шары с числом l_n, есть

.

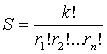Доказательство. Количество всевозможных извлечений k шаров из урны с возвращением, при которых были извлечены r₁ шары с числом l₁ , r₂ шары с числом l₂ , и так далее, r _n шары с числом l_n, есть полиномиальный коэффициент

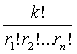
(см [1] стр.12). Теорема доказана.

Теорема 3. Вероятность того, что при последовательном извлечение k шаров из урны с возвращением, были извлечены r₁ шары с числом l₁ , r₂ шары с числом l₂ , и так далее, r _n шары с числом l_n, есть

,

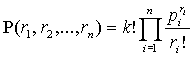где значения p₁, … , p_n определяют вероятности (или частности) появления шара с соответствующим числом l₁, l₂, ..., l_n.

Доказательство. Вероятность того, что при последовательном извлечение k шаров из урны с возвращением, были извлечены r₁ шары с числом l₁ , r₂ шары с числом l₂ , и так далее, r _n шары с числом l_n, есть полиномиальная вероятность (см [2] стр.84), которая представляется как

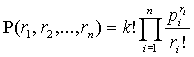. (2)

Теорема доказана.

Пример 2. Урна содержит 20 шаров, и каждый шар в урне помечен одним из возможных чисел 5, 7, 11, причем 6 шаров с числом 5, 10 шаров с числом 7 и 4 шара с числом 11. Извлекли из урны с возвращением 5 шаров. Какова вероятность, что при извлечении 1 шар будет с числом 5 и 4 шара с числом 7?

Решение. Из примера 1 имеем N=20, l₁=5, l₂=7, l₃=11, m₁=6, m₂=10, m₃=4, Подставим эти значения в формулу (2) при k=5, и получаем

.

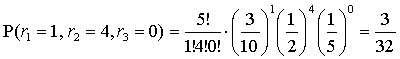Ответ: .

Список используемой литературы

1. Дж. Риодан. Введение в комбинаторный анализ. Перевод с англ. Л.Е. Садовского. М.: изд. Ин. лит. 1963 г. 287 с.

2. Кремер Н.Ш. Теория вероятностей и математическая статистика. Москва: Юнити. 2006 г., 571 с.

3. Савельев Л.Я. Комбинаторика и вероятность. М.: Наука. 1975.– 424с.

4. Panaretos J., Xekalaki E. On generalized binomial and multinomial distributions and their relation to generalized Poisson distributions. // Ann. Inst. Math. 1986.V.38.Part A. P. 223 – 231.

5. Искакова А.С. Об одном классе многомерных дискретных распределений вероятностей сумм прямоугольных матриц. // Известия МОН РК, НАН РК. 2001 г. № 5. С.85–89.

6. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84.