Аналіз енергетично оптимальних імпульсів активації

Аналіз енергетично оптимальних імпульсів активації

Дрипан Ю.А., Скапа І.В., Дрипан Н.Е.

Кременчуцький національний університет імені Михайла

Остроградського

У статті наведені деякі результати обчислень за отриманими співвідношеннями для форми енергетично оптимальних імпульсів активації, їх енергій та аналогічних характеристик сигналів на виході моделі нейрона.

Ключові слова: електропунктура, інтегративна медицина, імпульс активації, множник Лагранжа, характеристики «імпульс-тривалість».

Вступ

Незважаючи на успіхи сучасної біології, медицини і фармакології, проблеми профілактики, ранньої діагностики і оптимального лікування захворювань продовжують залишатися актуальними. Медицина практично завжди має справу з патологічним процесом, що вже склався, на тій або іншій стадії, коли тривалі функціональні розлади викликають переродження тканей і стають помітні зміни на рівні органу або системи. Існуючі аналітичні методики контролю параметрів органів, тканин і біологічних рідин не забезпечують можливість відстежити патологічний процес на початковому, так званому безсимптомному, доклінічному етапі (передхвороба), етапі виникнення функціональних відхилень від норми, які з часом дають незворотні зміни внутрішніх органів.

Практично всі процеси в організмі супроводжуються зміною електро-магнітних характеристик, які можуть бути зафіксовані різноманітними контактними і безконтактними фізичними способами. Одним з таких способів є електропунктурна діагностика, заснована на вимірюванні електрошкіряних характеристик [2].

Найбільш поширені в даний час і вельми перспективні електропунктурні методики (Накатані, Фоля, аурікулярні і т.п.) вимірюють шкірно-гальванічну реакцію за допомогою контактних металевих електродів із зондуючою напругою певного знаку (у методиці Накатані негативного, Фоля - позитивного). При цьому забезпечуючи відносну стабільність перехідного контактного опору в області прилягання шкіри з вимірювальним електродом [2,6]. Зазвичай, у основі електропунктурних методик лежать емпірично підібрані параметри схеми електровимірювання.

У всіх електропунктурних діагностичних вимірюваннях шкіра є перехідним елементом для зовнішнього вимірювального ланцюга. Як відомо, шкіра володіє чутливістю в широкому діапазоні спектру електромагнітних хвиль [2,4], здійснюючі активну енергетичну та інформаційну взаємодію організму із зовнішнім середовищем. Як орган, шкіра являє собою одну з найдавніших біосистем організму, починаючи від простих і кінчаючи ссавцями і людиною. Певно, система авторегуляції різних біохімічних процесів, що відбуваються в шкірі, закладається ще на ембріональній стадії розвитку людського організму і на початковому етапі має досить просту структуру, яка в свою чергу органічно пов'язана з довколишніми зачатками різних органів і частин тіла, а потім, розвиваючись разом з організмом, приймає складний, розгалужений характер [6]. Таким чином можна пояснити появу рефлексогенних реакций в певних місцях на шкірі при впливі на різні внутрішні органи.

Відсутність належної методології системного підходу і відповідних їй методів і апаратури, а також спрямованість діяльності практичного лікаря на оцінку, в основному, органних порушень не дає можливості реалізувати ефективну профілактичну стратегію і тактику ранньої діагностики і, тим самим, перейти на якісно інший рівень в медичному обслуговуванні.

Для оцінки загального функціонування організму як системи, що володіє розвиненими адаптаційними і резервними можливостями, вельми необхідним є загальносистемний критерій, що характеризує "правильність" функціонування всього організму, і оцінка стійкості всієї системи, що може трактуватися, як "запас здоров'я".

В рамках загальносистемного підходу людський організм - складна багаторівнева система з авторегулюванням, яка підтримує стійку сталість (у певних межах) життєво важливих параметрів внутрішнього середовища організму (гомеостаз) і активне його функціонування в зовнішньому середовищі, а також необхідний перерозподіл енергетичних ресурсів і адекватну реакцію на зовнішні й внутрішні стимули. Для повноти модельного уявлення потрібно враховувати той факт, що багато внутрішніх параметрів цієї системи безпосередньо пов'язано з фізичними характеристиками зовнішнього середовища і схильні до її збурень, здатним суттєво порушити стійкий динамічний стан системи, а іноді й зруйнувати її функціонування [11].

Кількісний моніторинг дисбалансів організму дозволяє виявити слабкі ланки в системі авторегуляції, які знаходяться на межі стійкості, можуть потрапити в екстремальну ситуацію і понизити запас стійкості всієї системи. Дані такого моніторингу визначають тактику корекції функціонального стану системи у напрямі середини діапазону стійкості, знижуючи тим самим ризик екстремальної ситуації. Реалізація такого принципу зовнішнього регулювання дозволяє працювати з істотно меншою помилкою регулювання системи зворотного зв'язку і не дозволить (за нормальних умов) функціональним відхиленням перейти до порушень органів і систем.

Розробка методів і апаратури для кількісного системного моніторингу дозволить реалізувати оптимальну стратегію ранньої діагностики і корекції патології на доклінічному етапі. Для вирішення цієї проблеми в рамках системного підходу необхідно знайти ті кількісні характеристики, на підставі яких можна судити про функціонування організму в цілому.

Основні матеріали та результати дослідження

Ч и с л о в і п а р а м е т р и о п т и м а л ь н и х і м п у л ь с і в а к т и в а ц і ї. Багатий позитивний клінічний досвід співробітників кафедри неврології і рефлексотерапії Національної медичної академії післядипломної освіти ім. П.Л. Щупика на чолі з чл.-кор. АМН України, д.м.н. Мачерет Є.Л.,а також результат плідної співпраці кафедр біомедичних електронних пристроїв та систем (ХНУРЕ), завідувач академік Академії прикладної радіоелектроніки, д.ф.-м.н. Бих А.І.,та електронних апаратів (КНУ ім. Михайла Остроградського).завідувач к.т.н. Мосьпан В.О.,дозволили створити і презентувати на І-му Українсько-китайському форумі (Харків,ХНУРЕ,2006) біполярний акупунктурний пристрій для ранньої діагностики та лікування маститів. Подальша співпраця у галузі інтегратативної медицини призвела до розробки сучасних апаратних методів акупунктурної діагностики та лікування, які допомагають швидко визначити стан функціональної активності меридіанів, а відповідно до цього й функціональних систем організму, поставити акупунктурний діагноз і вірно скласти акупунктурний рецепт, а також своєчасно зорієнтуватися у ефективності комплексного лікування. Саме для цього й були проведені обчислення для визначення енергетично оптимальних імпульсів активації нашого запатентованого біполярного пристрою.

Метою даної роботи було дослідження можливості ранньої діагностики та комплексного лікування маститів при моделюванні впливу на БАТ імпульсами різної форми та амплітуди.

Далі наведені деякі результати обчислень за отриманими співвідношеннями для форми енергетично оптимальних імпульсів, їх енергій та аналогічних характеристик сигналів на виході моделі нейрона. Значення нормованих коренів характеристичного рівняння та для систем рівнянь в залежності від нормованої тривалості вхідного імпульсу 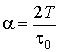() зведені до таблиць 1-4. Ці результати були отримані для значень параметрів фільтра ; , які отримуються при гіперболічній апроксимації характеристики “амплітуда-тривалість”, та значень ; , що відповідають експоненціально-гіперболічній характеристиці[10].

Крім того, в таблицях наведені нормовані значення множника Лагранжа , що є однаковими як для , так і для , та відношення енергії вхідного сигналу до енергії вихідного, яка вважається сталою.

Таблиця 1 - Корені характеристичного рівняння в залежності від

для розкладу за косинусами (; )


0.1	0.288	10.61	140.7	126.6	3	1.063	2.871	37.38	33.43
0.2	0.410	7.434	83.44	74.64	4	1.242	2.457	35.58	31.82
0.3	0.503	6.069	65.08	58.20	5	1.289	2.367	35.27	31.54
0.4	0.576	5.301	56.43	50.47	6	1.307	2.334	35.16	31.44
0.5	0.633	4.821	51.65	46.19	7	1.385	2.203	34.78	31.10
0.6	0.677	4.508	48.78	43.62	8	1.440	2.119	34.57	30.91
0.7	0.709	4.300	47.00	42.03	9	1.448	2.108	34.54	30.89
0.8	0.733	4.165	45.89	41.04	10	1.465	2.083	34.49	30.84
0.9	0.748	4.080	45.21	40.43	20	1.600	1.907	34.20	30.59
1	0.757	4.030	44.82	40.08	30	1.649	1.851	34.15	30.54
2	0.820	3.720	42.52	38.02	40	1.672	1.825	34.13	30.52

Таблиця 2 - Корені характеристичного рівняння в залежності від

для розкладу за синусами (; )


0.1	0.089	34.49	1217	1089	3	1.121	2.721	36.66	32.79
0.2	0.165	18.52	371.2	331.9	4	1.146	2.662	36.40	32.55
0.3	0.233	13.08	199.1	178.0	5	1.270	2.403	35.39	31.65
0.4	0.297	10.28	133.9	119.7	6	1.365	2.234	34.86	31.18
0.5	0.356	8.563	101.5	90.73	7	1.385	2.203	34.77	31.10
0.6	0.413	7.387	82.74	73.99	8	1.402	2.176	34.70	31.04
0.7	0.467	6.527	70.82	63.34	9	1.456	2.095	34.51	30.87
0.8	0.520	5.869	62.72	56.09	10	1.489	2.050	34.42	30.78
0.9	0.570	5.349	56.94	50.92	20	1.603	1.903	34.20	30.58
1	0.619	4.927	52.66	47.10	30	1.646	1.854	34.15	30.54
2	0.999	3.053	38.32	34.27	40	1.670	1.826	34.13	30.52

Таблиця 3 - Корені характеристичного рівняння в залежності від

для розкладу за косинусами (; )


0.1	0.256	7.820	66.22	3	0.789	2.534	12.05
0.2	0.357	5.597	36.45	4	0.933	2.145	10.47
0.3	0.431	4.636	26.68	5	1.031	1.940	9.826
0.4	0.490	4.084	21.92	6	1.063	1.881	9.669
0.5	0.537	3.724	19.16	7	1.067	1.875	9.653
0.6	0.576	3.475	17.40	8	1.101	1.817	9.513
0.7	0.607	3.294	16.22	9	1.149	1.741	9.351
0.8	0.632	3.162	15.40	10	1.176	1.700	9.274
0.9	0.653	3.065	14.82	20	1.274	1.570	9.088
1	0.668	2.993	14.40	30	1.315	1.521	9.042
2	0.703	2.845	13.59	40	1.340	1.492	9.023

Таблиця 4 - Корені характеристичного рівняння в залежності від

для розкладу за синусами (; )


0.1	0.061	32.85	1084	3	0.913	2.190	10.63
0.2	0.117	17.09	297.2	4	0.946	2.114	10.37
0.3	0.169	11.82	144.7	5	0.962	2.079	10.25
0.4	0.218	9.163	89.01	6	1.033	1.936	9.815
0.5	0.265	7.559	62.21	7	1.102	1.816	9.510
0.6	0.309	6.483	47.12	8	1.132	1.767	9.404
0.7	0.350	5.708	37.70	9	1.135	1.763	9.395
0.8	0.390	5.123	31.40	10	1.150	1.740	9.348
0.9	0.429	4.666	26.95	20	1.275	1.568	9.086
1	0.465	4.298	23.69	30	1.320	1.516	9.039
2	0.758	2.639	12.54	40	1.340	1.492	9.023

Як видно з наведених таблиць, множник Лагранжа, який визначає співвідношення енергій вхідного та вихідного сигналів, в залежності від значення нормованої тривалості вхідного імпульсу , може бути більшим або для розкладу за синусами, або для розкладу за косинусами.

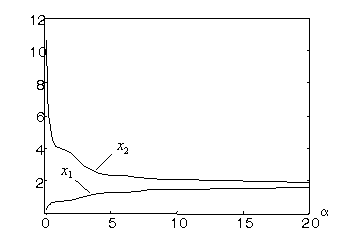
На рис. 1-2 представлені графіки залежності нормованих коренів та характеристичного рівняння від параметра при ; для розкладів за косинусами та синусами.

Рисунок 1 - Залежність коренів характеристичного рівняння та від нормованої тривалості імпульсу для розкладу за косинусами

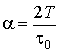Рисунок 2 - Залежність коренів характеристичного рівняння та від нормованої тривалості імпульсу для розкладу за синусами.

На рис. 3 - 4 наведені графіки залежності множників Лагранжа від нормованої тривалості імпульсу для двох варіантів значень та .

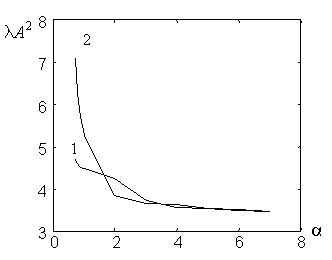
Рисунок 3 - Залежність нормованих множників Лагранжа від нормованої тривалості вхідного імпульсу для розкладу за косинусами (крива 1) та синусами (крива 2) при ; ;

Рисунок 4 - Залежність нормованих множників Лагранжа від нормованої тривалості вхідного імпульсу 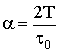для розкладу за косинусами (крива 1) та синусами (крива 2) при ;

Як видно з наведених графіків, існують окремі діапазони значень нормованих тривалостей вхідних імпульсів, за яких оптимальними імпульсами є розклади за косинусами (менше значення ), а в інших діапазонах значень оптимальні розклади за синусами.

В а р і а н т и е н е р г е т и ч н о о п т и м а л ь н и х і м п у л ь с і в п р и р о з к л а д а х з а к о с и н у с а м и. На рис.5 - 8 наведені графіки енергетично оптимальних вхідних імпульсів для моделі нейрона при розкладах за косинусами, а також відповідні їм вихідні сигнали при та .

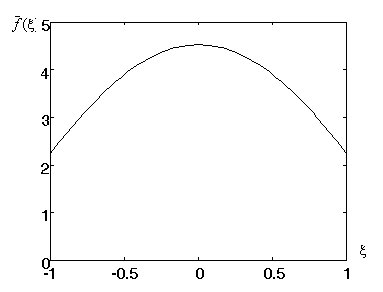
Рисунок 5 - Оптимальний імпульс активації для розкладу за косинусами при

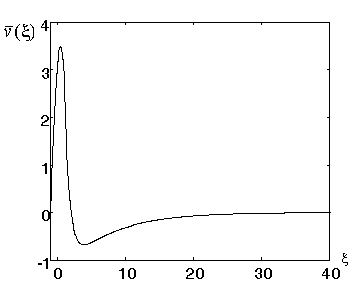
Рисунок 6 - Вихідний сигнал для розкладу за косинусами при

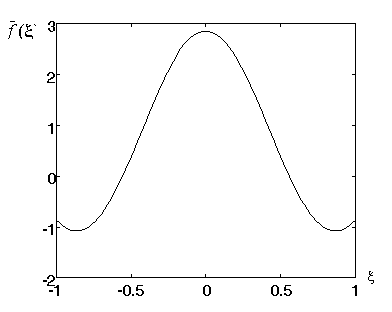
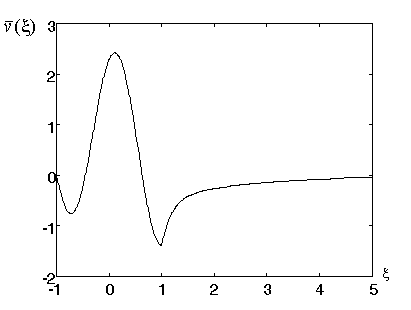
Рисунок 7 - Оптимальний імпульс активації для розкладу за косинусами при

Рисунок 8 - Вихідний сигнал для розкладу за косинусами при

Як видно з наведених графіків, вихідний сигнал при за формою близький до нейроімпульсу, при збільшенні як вхідний, так і вихідний сигнали стають все більш коливальними.

Результати дослідження

П р и к л а д и е н е р г е т и ч н о о п т и м а л ь н и х і м п у л ь с і в п р и р о з к л а д а х з а с и н у с а м и. На рис. 9 - 12 наведені аналогічні графіки енергетично оптимальних вхідних імпульсів для моделі нейрона при розкладах за синусами та відповідні їм вихідні сигнали при та .

Рисунок 9 - Оптимальний імпульс активації для розкладу за синусами при

Рисунок 10 - Вихідний сигнал для розкладу за синусами при

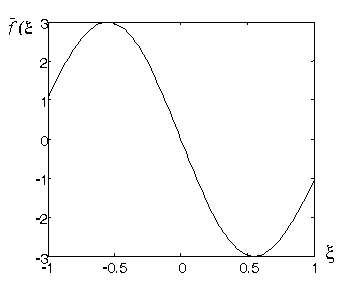
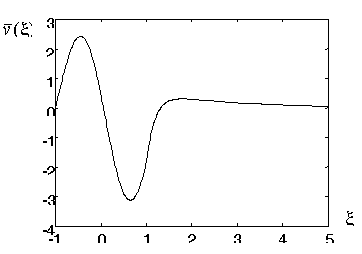
Рисунок 11 - Оптимальний імпульс активації для розкладу за синусами при

Рисунок 12 - Вихідний сигнал для розкладу за синусами при

Х а р а к т е р и с т и к и “а м п л і т у д а – т р и в а л і с т ь” д л я е н е р г е т и ч н о о п т и м а л ь н и х і м п у л ь с і в а к т и в а ц і ї. На основі отриманих результатів можна побудувати аналог характеристики “амплітуда-тривалість” для оптимальних за енергією імпульсів активації. Ця характеристика являє собою залежність між амплітудою (максимальним значенням) вхідного імпульсу порогової активації та його тривалістю, за яких енергія вихідного сигналу залишається сталою. На рис. 13 наведена

така характеристика для косинусоподібних імпульсів активації.

Рисунок 13 - Характеристика “амплітуда-тривалість” для косинусоподібних імпульсів активації

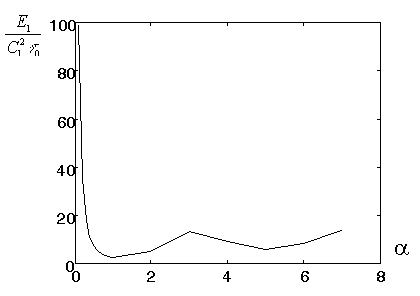
Рисунок 14 – Залежність нормованої енергії вхідного сигналу від нормованої тривалості імпульсу при розкладі за косинусами

Енергетичні особливості оптимальних косинусоподібних вхідних імпульсів активації відображені на графіках на рис. 14-15, де представлено залежності нормованих енергій вхідного сигналу від нормованої його тривалості, причому другий графік відображає цю енергетичну залежність при фіксованій енергії вихідного сигналу.

Рисунок 15 - Залежність нормованої енергії вхідного сигналу при фіксованому рівні енергії вихідного сигналу від нормованої тривалості імпульсу при розкладі за косинусами

Як видно, з вище наведених графіків, їх якісний характер відповідає традиційним характеристикам “амплітуда-тривалість” (зі зростанням тривалості вхідного імпульсу порогової активації його амплітуда зменшується), однак варто звернути увагу, що в деяких діапазонах тривалостей спостерігається деяке зростання амплітуди зі збільшенням тривалості. Це можна пояснити тим, що при зміні тривалості імпульсу змінюється його форма і в деяких діапазонах значень тривалості зміна форми має більший вплив на енергетичні параметри сигналу, ніж його тривалість.

Таким самим чином можна отримати аналогічні графіки енергетичних властивостей оптимальних імпульсів активації при розкладі за синусами. Ці графіки мають якісно такий самий характер.

Висновки

Таким чином, на основі проведеного аналізу можна зробити наступні висновки. Як при розкладах за косинусами, так і за синусами, оптимальні вхідні імпульси є симетричними. Для коротких імпульсів (тривалість імпульсу ) оптимальний імпульс близький до відрізка косинусоїди з тривалістю, набагато меншою за період. В результаті такий імпульс близький до прямокутного. При зростанні тривалості імпульсу він набуває все більш коливального характеру, причому в деякому діапазоні часових співвідношень оптимальний імпульс має двополярний характер, тобто має лише одну додатну і одну від’ємну півхвилі. Саме для імпульсів такої форми експериментально була встановлена їх ефективність в ряді задач активації, зокрема, електронейро- та електроміостимуляції, а також при дефібриляції серця.

ЛІТЕРАТУРА:

1. Патент України № 24914 на корисну модель: Пристрій для акупунктурної діагностики та лікування. Зареєстровано в Державному реєстрі патентів України 25 липня 2007р.

2.Мачерет Е.Л., Коркушко О.О. Основы электроакупунктуры.- К.: Здоров’я,1993.-385с.

3.Табеева Д.М. Руководство по иглорефлексотерапии.- М.: Медицина,1980.-560с.

4. Ходжкин А. Нервный импульс. – М.: Мир, 1965. – 127 с.

5. Богач П.Г., Клевець М.Ю., Рибальченко В.К. Основи електрофізіології. – К.: Вища шк. Головне вид-во, 1984. – 231 с.

6.Лувсан Г. Очерки методов восточной рефлексотерапии. – Новосибирск.: Наука, 1991. – 432с.

7. Дьяконов В., Абраменкова И. MATLAB. Обработка сигналов и изображений. Специальный справочник. – СПб.: Питер, 2002. – 608 с.

8. Дьяконов В., Круглов В. Математические пакеты расширения MATLAB. Специальный справочник. – СПб.: Питер, 2001. – 480 с.

9. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров: Пер. с англ. - М.: Наука. Гл. ред. физ.-мат. лит., 1970. – 720 с.

10. Романишин Ю.М. Аналіз активації нейрона енергетично оптимальними імпульсами // Збірник наукових праць Інституту проблем моделювання в енергетиці ім. Г.Є. Пухова НАН України. Випуск 27. – Київ. - 2004. – С. 74-80.

11. Романишин Ю.М., Смердов А.А. Отримання характеристики “сила-тривалість” на основі частотновибірної моделі процесу збудження нейрону // Фізика живого. – 2003. – Т. 11, № 2. – С. 52-60.

12. Справочник по специальным функциям (с формулами, графиками и математическими таблицами) / Под ред. М. Абрамовица и И. Стиган: Пер. с англ. Под ред. В.А. Диткина и Л.Н. Кармазиной. - М.: Наука. Гл. ред. физ.-мат. лит., 1979. – 830 с.

13.Тасаки И. Нервное возбуждение. Макромолекулярный подход: Пер. с англ. Под ред. Б.И. Ходорова и Ю.А. Чизмаджева. – М.: Мир., 1971. – 222 с.

14.Тасаки И. Проведение нервного импульса. - М.: ИИЛ, 1957. – 186 с.

Дрипан Юрій Анатолійович, старший викладач кафедри «Електронні апарати».

Кременчуцький національний університет імені Михайла Остроградського.

Скапа Іван Васильович, старший викладач кафедри «Вища математика і інформатика».

Кременчуцький національний університет імені Михайла Остроградського.

Дрипан Наталія Євгенівна, лікар невропатолог 1-ї категорії.

Кременчуцька міська лікарня №1.