Òåõíè÷åñêèå íàóêè / 12. Àâòîìàòèçèðîâàííûå ñèñòåìû
óïðàâëåíèÿ íà ïðîèçâîäñòâå
Kulyk A.J., Kulyk J.A, Kulyk A.A.
Vinnytsia national technical
university, Ukraine
Select noiseproof codes for information transmission lines
collective
Download lines shared, and the first telephone
network is constantly growing. Great information transmitted via modems with
high level industrial noise, require efficient protocols and algorithms
exchange related noiseproof encoding.
Messages must be transmitted to the communication line, consisting of
information Ð and
service  in parts
L = P + B .
(1)
The first one
contains the information that is transmitted and the second – post office
protocol, routing, etc.
Principle of the noiseproof coding is to build redundancy
– the formation of additional control bits. Depending on the code distance d
code can have different functionality
d = r + s + 1 (r ³ s) , (2)
where r – number of errors identified;
s – number of errors corrected.
To correct one
error code need a code with distance d = 3, and to correct two mistakes
– with code distance d = 5.
So after noiseproof encoded message length L is increased by
control bits K
Ì = L + Ê . (3)
Often used block coding principle, when the original message is divided
into L number of blocks L1, L2, L3, … , Ln and each of them attached appropriate combination of
control bits K 1, K 2, K 3, ..., K n
.
Because most of the lines of collective use of information transmitted
using modems with PCs, then there are some features to consider:
Ä
serial interface used to transfer information to the communication line,
mostly working with bytes. Even if the number of bits can be programmed as for
basis chip Intel 8251 (KP580BB51), the port can still follow the word with
zeros to complete the communication line is transmitted 8 bits;
Ä
to signals transmitted to the communication line can adversely affect
the external factors that vary by season, time of day, weather conditions,
congestion, lines, etc. and have a random character;
Ä
using linear (sequential) code type Manchester II, AMI, BNZS, HDB3 so
pointless, because they only fix bugs, not correcting them, require significant
hardware costs and difficult program implemented;
Ä
analysis of errors arising during transmission and not distort the
information held, and hold it is necessary for each specific area separately
based on individual characteristics of the network.
This led to what size unit code combinations practically defined.
Preliminary analysis of adopted information transmitted telephone
network of Vinnitsa without noiseproof codes, showed that at speeds of 1200 and
2400 bps skewed a bit about a hundred. Use of the noiseproof codes (cyclic,
Hemming etc.) requires an assessment number and the number of informative bits
errors are corrected. The ratio of information and control bits for words of
varying lengths given in tab. 1.
During the building code to correct two errors the number of control
bits increases unreasonably, causing one of the major challenges for the
delivery and on the other - increasing the probability of distortion of information.
The probability of accurate exchange of information considered for the
simplest case (independence of errors that arise in a symmetric channel). The
probability of error-free transmission will be determined:
ðïð = 1 – ðïîì . (4)
where ð ïîì – the error probability.
Table 1 –
Correlation of information and control bits
|
Word length |
d = 3 |
d = 5 |
||
|
Number of control bits |
The total number of bits |
Number of control bits |
The total number of bits |
|
|
1 |
2 |
3 |
|
|
|
2 |
3 |
5 |
4 |
6 |
|
3 |
3 |
6 |
5 |
8 |
|
4 |
3 |
7 |
9 |
13 |
|
5 |
4 |
9 |
|
|
|
6 |
4 |
10 |
||
|
7 |
4 |
11 |
||
|
8 |
4 |
12 |
||
|
9 |
4 |
13 |
||
|
10 |
4 |
14 |
||
|
11 |
4 |
15 |
||
|
12 |
5 |
17 |
||
For a system that uses the principle of error correction coding, the
Bernoulli formula [1]
where ð 0 – the error probability;
k – number of errors corrected code;
m – total number of characters.
Another method [2] developed by L. Purtov,
The calculation results for both methods are tabulated in tab. 2. They
show that already at eight characters method for determining the probability of
the Bernoulli formula does not work because the error probability is much
greater than one.
Table 2 –
Probability of accurate information
transfer for words of different length
|
Number of information bits |
The total number of bits |
d = 3 |
d = 5 |
||
|
For Bernoulli |
For Purtov |
For Bernoulli |
For Purtov |
||
|
1 |
3 |
0,99985 |
0,97 |
|
|
|
2 |
5 |
0,997 |
0,95 |
0,99993 |
0,985 |
|
3 |
6 |
0,983 |
0,94 |
0,89 |
0,96 |
|
4 |
7 |
0,88 |
0,93 |
Method does not work |
0,935 |
|
5 |
9 |
Method does not work |
0,91 |
Method does not work |
|
|
6 |
10 |
0,9 |
|||
|
7 |
11 |
0,89 |
|||
|
8 |
12 |
0,88 |
|||
|
9 |
13 |
0,87 |
|||
|
10 |
14 |
0,86 |
|||
|
11 |
15 |
0,85 |
|||
|
12 |
17 |
0,83 |
|||
The calculations were carried out taking into account the previous
analysis garbled probability ( ð 0 » 0,01). The analysis confirms that the form code to correct
two or more errors is pointless, because the probability of distortion due to
increase in number of characters covers bug fixes.
On the transfer efficiency significantly affect the exchange. In adverse
conditions does not exceed the speed of 4800 bps, but actually is 2400 bps. To
speed this time sending one kilobit (128 bytes of information) for words of
different length with the principles of serial interfaces listed in the tab. 3.
Table 3 –
Time of transfer words varying lengths
|
||||||||||||||||||||||||||||||||||||||
|
|
Table 4 –
Time of transfer words of different length, provided re bytes
|
|
|
 Given the features
of the serial interface to the appropriate transfer necessary the change
information structure bytes, complementing the number and control bits to
eight, adding the necessary amount from the next byte. At the same time
transfer significantly reduced. The results of such calculations for similar conditions
are given to the tab. 4. For illustrative graphs calculated parameters appropriate
place in the same coordinate system.
Given the features
of the serial interface to the appropriate transfer necessary the change
information structure bytes, complementing the number and control bits to
eight, adding the necessary amount from the next byte. At the same time
transfer significantly reduced. The results of such calculations for similar conditions
are given to the tab. 4. For illustrative graphs calculated parameters appropriate
place in the same coordinate system.
Their analysis leads to certain conclusions:
ü
for transmitting information necessary to build the code for correcting
a mistake;
ü
be the most efficient transmission by half bytes with the addition of
three control to four bits of information;
ü
before transmission necessary the change information structure,
complementing the next level with up to eight bytes.
REFERENCES:
1.
Êóçüìèí È.Â., Êëþ÷êî Â.È., Ëèòâèí Â.À. Êîäèðîâàíèå è äåêîäèðîâàíèå â
èíôîðìàöèîííûõ ñèñòåìàõ. – Ê.: Âèùà øêîëà, 1985, 190 ñ.
2.
Ýëåìåíòû
òåîðèè ïåðåäà÷è äèñêðåòíîé èíôîðìàöèè / ïîä ðåä. Ïóðòîâà Ë.Ï. – Ì.: Ñâÿçü,
1972, 232 ñ.
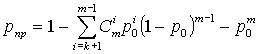 ,
,