2 Механика

В.Н. Украинец

Павлодарский государственный университет им. С. Торайгырова, Павлодар, Казахстан, e-mail:vitnikukr@mail.ru.

Сравнительный анализ действия бегущей нагрузки на расположенную в упругом полупространстве оболочку при ее различных моделях

В работах [1,2] решены задачи о действии подвижной нагрузки на бесконечно длинную круговую цилиндрическую оболочку в упругом полупространстве. В [1] получено точное решение, когда движение оболочки и окружающей среды описываются динамическими уравнениями теории упругости, а в [2] – приближенное решение, основанное на классической теории тонких оболочек. В настоящей работе проводится сравнительный анализ результатов расчета напряжённо-деформированного состояния (НДС) окружающего оболочку массива, полученных на основе данных решений.

Следуя [1,2], рассмотрим бесконечно длинную круговую цилиндрическую оболочку, расположенную в линейно-упругом, однородном и изотропном полупространстве параллельно его ненагруженной горизонтальной границе . Оболочка может быть толстостенной, с радиусами наружной и внутренней поверхностей соответственно R₁ и R₂, или тонкостенной (в этом случае, в силу малости толщины оболочки h₀ полагаем, что окружающий массив контактирует с оболочкой вдоль её срединной поверхности, то есть R₁ = R, где R – радиус кривизны срединной поверхности оболочки). Контакт между оболочкой и окружающим её массивом полагаем либо жестким, либо скользящим при двусторонней связи в радиальном направлении. На внутреннюю поверхность оболочки действует нагрузка интенсивностью Р, движущаяся с постоянной скоростью с в направлении её оси, совпадающей с осью z декартовой системы координат xyz. Скорость движения нагрузки принимаем дозвуковой, т. е. меньше скоростей распространения волн сдвига в толстостенной оболочке и окружающей упругой среде. Так как рассматривается установившийся процесс, то картина деформаций стационарна в связанной с нагрузкой подвижной системе декартовой (x, y, h = z - ct) или цилиндрической (r, q, h = z - ct) системе координат. Физико-механические свойства материала массива и толстостенной оболочки характеризуются соответственно следующими постоянными: n₁, m₁, r₁; n₂, m₂, r₂, где n_k – коэффициент Пуассона, m_k – модуль сдвига, r_k – плотность, (k = 1, 2). В дальнейшем индекс k = 1 относится к массиву, а k = 2 – к толстостенной оболочке. Аналогичные обозначения (n₀, m₀, r₀) принимаем для характеристик материала тонкостенной оболочки.

Для описания движения массива и толстостенной оболочки используем динамические уравнения теории упругости, которые в векторной форме имеют вид

, (1)

где M_pk = c/c_pk, M_sk = c/c_sk – числа Маха, c_pk = [(l_k + 2m_k)/r_k]^1/2, c_sk = (m_k/r_k)^1/2 – скорости распространения волн расширения – сжатия и сдвига в массиве и оболочке, l_k = 2m_kn_k/(1–2n_k); u_k – векторы смещений точек массива и оболочки, Ѳ – оператор Лапласа.

Движение тонкостенной оболочки описывается классическими уравнениями теории тонких оболочек

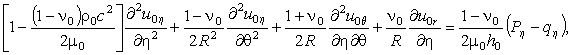
(2)

,

где u_0h, u_0q, u_0r – перемещения точек срединной поверхности оболочки, P_j(q,h) – составляющие интенсивности подвижной нагрузки P(q,h), – составляющие реакции окружающего оболочку массива (при скользящем контакте оболочки с массивом q_h = q_q = 0), s_rj1 – компоненты тензора напряжений в среде, j = h ,q, r.

Векторы u_k можно выразить через потенциалы Ламе

, (3)

которые, как следует из (1) и (3), удовлетворяют уравнениям

, (4)

где М_1k = М_pk, М_2k = М_3k = М_sk.

Рассмотрим вначале подвижную нагрузку с произвольной зависимостью от угловой координаты и изменяющуюся вдоль h синусоидально

; . (5)

В установившемся состоянии зависимость всех величин от h имеет вид (5), поэтому j_jk(r, q, h) = F_jk(r, q)e^ixh,

(6)

где – двумерный оператор Лапласа,

. (7)

Выразив компоненты НДС массива и толстостенной оболочки через потенциалы Ламе можно получить выражения для перемещений и напряжений (* означает, что данные компоненты соответствуют решению периодической задачи) от синусоидальной нагрузки в цилиндрической (l, m = r,θ,η; k = 1, 2) и декартовой (l, m = x,y,η; k = 1) системах координат как функции от . Определим эти функции.

При дозвуковой скорости нагрузки M_sk < 1, k = 1, 2, и решения (6) можно представить в виде

, (8)

где:

- для полупространства

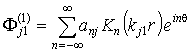, ; (9)

- для оболочки

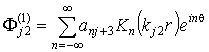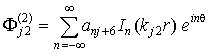, . (10)

Здесь – соответственно модифицированные функции Бесселя и функции Макдональда, , , j = 1,2,3; g_j(x,z), – неизвестные функции и коэффициенты, подлежащие определению.

Представление потенциалов для полупространства в форме (9) приводит к их следующим выражениям в декартовой системе координат:

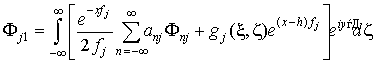, (11)

где .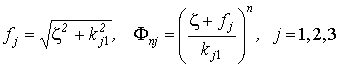

Воспользуемся, с учётом (11), граничными условиями для свободной от нагрузок поверхности полупространства (x = h)

.

Выделяя коэффициенты при e^iyζ и приравнивая, в силу произвольности y, их нулю, получим систему трёх уравнений, из которой выражаем g_j(ξ,ζ) через коэффициенты a_nj:

. (12)

Вид определителя D^* и алгебраических дополнений D^*_jl совпадает с аналогичными определителями для неподкрепленной полости в упругом полупространстве и определён в [3]. В частности, здесь D^* – это определитель Рэлея, который в данном случае имеет вид

,

и не обращается в ноль при любых z, если скорость бегущей нагрузки меньше скорости рэлеевской волны c_R в полупространстве. В противном случае в точках он обращается в ноль, и интегралы в формуле (11) становятся расходящимися.

Пусть . В этом случае все подынтегральные функции в (11) непрерывны и экспоненциально стремятся к нулю на бесконечности. С учетом (12), формулы (11) имеют вид

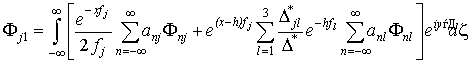. (13)

Воспользовавшись известным разложением [3], представим потенциалы для полупространства (8) в цилиндрической системе координат, используя (12)

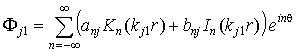, (14)

где , , .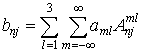

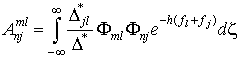Таким образом, решение периодической задачи для толстостенной оболочки в упругом полупространстве сводится к отысканию коэффициентов , для определения которых, в зависимости от условия сопряжения оболочки со средой, следует воспользоваться следующими граничными условиями:

- для поверхности полости и оболочки при скользящем контакте

при r = R₁ , , , , , ,

при r = R₂ , ; (15,а)

- для поверхности полости и оболочки при жёстком контакте

при r = R₁ , , при r = R₂ , . (15,б)

В случае тонкостенной оболочки решение упрощается. Из (2), с учётом (5) и (7), для n-го члена разложения можно получить систему линейных уравнений, из которой определяются

,

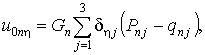
где , , . Для P_nj и q_nj индекс j = 1 соответствует индексу h, j = 2 – q, j = 3 – r. Коэффициенты d_lj(x), l = h, q, r и знаменатели d_n(x) определены в [2].

Неизвестные коэффициенты находятся из граничных условий:

- при скользящем контакте оболочки с массивом

; (16,а)

- в случае жёсткого сцепления оболочки с массивом

. (16,б)

Приравнивая в обоих случаях коэффициенты рядов Фурье-Бесселя при e^inq, получим бесконечную систему (n = 0, ±1, ±2,…) линейных алгебраических уравнений, для решения которой можно использовать метод редукции или более удобный для решения поставленной задачи метод последовательных отражений [3], позволяющий при каждом последовательном отражении решать систему линейных уравнений блочно-диагонального вида.

Зная решение задачи для синусоидальной нагрузки, реакцию оболочки и окружающей её среды на движущуюся с постоянной скоростью апериодическую (локальную) нагрузку) можно найти при помощи суперпозиции, используя представление нагрузки и компонент НДС оболочки и массива в виде интегралов Фурье [1,2]. Для вычислений перемещений и напряжений можно использовать любой численный метод интегрирования, если определители D_n(x, с) разрешающей блочно-диагональной системы линейных алгебраических уравнений отличны от нуля, т.е. когда скорость движения нагрузки c меньше её критических скоростей [2].

Рассмотрим стальную оболочку (n₀ = n₂= 0,3, m₀ = m₂= 8,08×10¹⁰Па, r₀ =r₂ = 7,8×10³кг/м³) толщиной h₀, расположенную в упругом полупространстве (n₁= 0,25, m₁ = m= 4,0×10⁹Па, r₁ = 2,6×10³кг/м³) при h = 2R, где R₁ = R = 1м. Движущаяся в оболочке с докритической и дорэлеевской скоростью c = 100 м/с осесимметричная нормальная нагрузка давления P_r, равномерно распределена в интервале |h| £ 0,2R. Интенсивность нагрузки выбираем таким образом, чтобы общая нагрузка по всей длине участка нагружения равнялась сосредоточенной нормальной кольцевой нагрузке P^°.

Данные расчётов НДС (u^°_r = u_rm/P^°, s^°_qq = s_qq/P^°, s^°_hh = s_hh/P^°) массива в контактных с оболочкой точках, r = R₁, h = 0 при разных h₀/R и условиях сопряжения приведены в табл. 1, где в скобках указаны значения компонент найденные по приближённой теории, а без скобок – по точной теории. Из таблицы следует, что при h₀/R = 0,02 и любом сопряжении оболочки с массивом погрешность для значений радиальных перемещений u_r найденных по точной и приближённой теориям не превышает пяти процентов, а для нормальных напряжений – четырнадцати процентов. С увеличением толщины h₀ в два с половиной раза (h₀/R = 0,05) погрешность для u_r возрастает в два раза как при жёстком, так и при скользящем контакте и составляет 9%, а нормальные напряжения при жёстком контакте отличаются уже в два раза, хотя при скользящем контакте их отличия незначительны. Причём, приближённая теория даёт завышенные значения компонент (исключение составляют тангенциальные напряжения s_θθ, при жёстком контакте).

Данные аналогичного расчёта поверхности полупространства помещены в табл. 2, где приведены значения компонент её напряжённо-деформированного состояния u^°_x= u_xm/P^°, u^°_y= u_ym/P,^° s^°_yy = s_yy/P^°, s^°_ηη = s_ηη/P^°. Здесь значения компонент найденных по приближённой теории ненамного больше, чем при использовании точной теории.

Табл. 1 – Компоненты НДС массива в контактных точках r = R₁, h = 0

h0/R	Комп. НДС	q, град
		0	20	40	60	80	100	120	140	160	180
Жёсткий контакт
0,02	u^°r	0,44 (0,45)	0,42 (0,44)	0,39 (0,41)	0,37 (0,38)	0,35 (0,36)	0,33 (0,35)	0,33 (0,35)	0,34 (0,35)	0,35 (0,36)	0,34 (0,36)
	s^°θθ	0,21 (0,18)	0,21 (0,19)	0,23 (0,23)	0,25 (0,24)	0,24 (0,23)	0,21 (0,21)	0,20 (0,19)	0,20 (0,17)	0,17 (0,15)	0,14 (0,14)
	s^°hh	-0,84 (-0,96)	-0,82 (-0,95)	-0,81 (-0,94)	-0,81 (-0,92)	-0,81 (-0,92)	-0,79 (-0,92)	-0,79 (-0,92)	-0,81 (-0,92)	-0,81 (-0,93)	-0,80 (-0,93)
0,05	u^°r	0,30 (0,33)	0,29 (0,32)	0,28 (0,30)	0,26 (0,28)	0,25 (0,27)	0,25 (0,27)	0,24 (0,27)	0,25 (0,27)	0,25 (0,27)	0,25 (0,27)
	s^°θθ	0,18 (0,11)	0,17 (0,11)	0,17 (0,12)	0,16 (0,12)	0,17 (0,11)	0,16 (0,11)	0,15 (0,10)	0,14 (0,09)	0,14 (0,08)	0,14 (0,08)
	s^°hh	-0,35 (-0,69)	-0,36 (-0,69)	-0,36 (-0,69)	-0,36 (-0,69)	-0,36 (-0,69)	-0,36 (-0,69)	-0,36 (-0,69)	-0,36 (-0,69)	-0,37 (-0,70)	-0,37 (-0,70)
Скользящий контакт
0,02	u^°r	0,46 (0,48)	0,45 (0,47)	0,41 (0,43)	0,38 (0,39)	0,36 (0,37)	0,35 (0,36)	0,35 (0,36)	0,35 (0,36)	0,36 (0,37)	0,36 (0,37)
	s^°θθ	-0,01 (-0,01)	0,03 (0,03)	0,10 (0,11)	0,14 (0,16)	0,13 (0,15)	0,11 (0,11)	0,07 (0,08)	0,03 (0,04)	0,0 (0,01)	-0,01 (0,0)
	s^°hh	-1,67 (-1,71)	-1,65 (-1,69)	-1,60 (-1,63)	-1,56 (-1,59)	-1,54 (-1,57)	-1,53 (-1,57)	-1,54 (-1,57)	-1,54 (-1,58)	-1,55 (-1,58)	-1,56 (-1,59)
0,05	u^°r	0,32 (0,35)	0,32 (0,34)	0,30 (0,32)	0,28 (0,29)	0,26 (0,28)	0,26 (0,27)	0,26 (0,27)	0,26 (0,28)	0,27 (0,28)	0,27 (0,29)
	s^°θθ	-0,08 (-0,08)	-0,06 (-0,06)	-0,07 (0,0)	0,01 (0,03)	0,0 (0,02)	-0,01 (0,0)	-0,03 (-0,02)	-0,06 (-0,05)	-0,07 (-0,07)	-0,07 (-0,08)
	s^°hh	-1,36 (-1,45)	-1,36 (-1,43)	-1,34 (-1,40)	-1,30 (-1,37)	-1,29 (-1,36)	1,29 (-1,36)	-1,29 (-1,36)	-1,29 (-1,37)	-1,30 (-1,37)	-1,31 (-1,37)

Табл. 2 – Компоненты НДС поверхности полупространства в плоскости XY

h0/R	Комп. НДС	y/R
		0,0	0,4	0,8	1,2	1,6	2,0	2,4	2,8	3,2
Жёсткий контакт
0,02	u^°x	0,18 (0,18)	0,17 (0,17)	0,13 (0,14)	0,10 (0,11)	0,10 (0,07)	0,07 (0,05)	0,05 (0,03)	0,02 (0,02)	0,02 (0,02)
	u^°y	0,0 (0,0)	0,04 (0,04)	0,06 (0,06)	0,06 (0,07)	0,06 (0,06)	0,05 (0,05)	0,04 (0,04)	0,03 (0,04)	0,03 (0,03)
	s^°yy	0,33 (0,35)	0,27 (0,29)	0,15 (0,15)	0,05 (0,03)	-0,02 (-0,04)	-0,05 (-0,04)	-0,04 (-0,03)	-0,04 (-0,03)	-0,04 (-0,04)
	s^°hh	0,37 (0,39)	0,34 (0,35)	0,26 (0,27)	0,18 (0,18)	0,12 (0,12)	0,08 (0,08)	0,05 (0,05)	0,04 (0,03)	0,02 (0,02)
0,05	u^°x	0,11 (0,12)	0,10 (0,11)	0,08 (0,09)	0,06 (0,07)	0,04 (0,05)	0,03 (0,03)	0,02 (0,02)	0,01 (0,01)	0,01 (0,01)
	u^°y	0,0 (0,0)	0,02 (0,02)	0,03 (0,04)	0,04 (0,04)	0,04 (0,04)	0,03 (0,03)	0,03 (0,03)	0,02 (0,02)	0,02 (0,02)
	s^°yy	0,21 (0,23)	0,17 (0,19)	0,10 (0,11)	0,03 (0,03)	-0,01 (-0,01)	-0,02 (-0,03)	-0,03 (-0,03)	-0,03 (-0,03)	-0,02 (-0,03)
	s^°hh	0,25 (0,28)	0,23 (0,25)	0,17 (0,19)	0,12 (0,13)	0,08 (0,08)	0,05 (0,05)	0,03 (0,03)	0,02 (0,02)	0,02 (0,02)
Скользящий контакт
0,02	u^°x	0,19 (0,21)	0,18 (0,20)	0,15 (0,16)	0,11 (0,11)	0,08 (0,07)	0,05 (0,05)	0,03 (0,03)	0,02 (0,02)	0,01 (0,02)
	u^°y	0,0 (0,0)	0,04 (0,04)	0,06 (0,06)	0,07 (0,07)	0,06 (0,06)	0,05 (0,05)	0,04 (0,05)	0,03 (0,04)	0,02 (0,03)
	s^°yy	0,36 (0,36)	0,30 (0,30)	0,16 (0,17)	0,04 (0,05)	-0,04 (-0,02)	-0,07 (-0,04)	-0,05 (-0,04)	-0,03 (-0,04)	-0,03 (-0,04)
	s^°hh	0,41 (0,43)	0,38 (0,39)	0,29 (0,29)	0,19 (0,20)	0,12 (0,13)	0,08 (0,08)	0,05 (0,05)	0,04 (0,04)	0,03 (0,03)
0,05	u^°x	0,13 (0,14)	0,12 (0,13)	0,09 (0,10)	0,07 (0,07)	0,05 (0,05)	0,03 (0,03)	0,02 (0,02)	0,01 (0,02)	0,01 (0,01)
	u^°y	0,0 (0,0)	0,03 (0,03)	0,04 (0,04)	0,04 (0,05)	0,04 (0,04)	0,03 (0,04)	0,02 (0,03)	0,02 (0,02)	0,01 (0,02)
	s^°yy	0,24 (0,25)	0,20 (0,21)	0,11 (0,12)	0,02 (0,03)	-0,02 (-0,02)	-0,04 (-0,03)	-0,03 (-0,03)	-0,02 (-0,04)	-0,02 (-0,04)
	s^°hh	0,29 (0,31)	0,26 (0,28)	0,20 (0,21)	0,13 (0,14)	0,08 (0,09)	0,05 (0,06)	0,04 (0,04)	0,02 (0,02)	0,02 (0,02)

Из анализа результатов очевидно, что для практических расчётов НДС массива в окрестности полости вполне допустимо применение классической теории тонких оболочек, если отношение толщины оболочки к радиусу её срединной поверхности меньше 0,05. Хотя для исследования НДС поверхности полупространства, этот диапазон, в зависимости от h, может быть шире.

Литература:

1 Алексеева Л.А., Украинец В.Н. Динамика подземных трубопроводов мелкого заложения под воздействием подвижных нагрузок //Механика и строительство транспортных сооружений: труды межд. науч.-практ. конф. Алматы, 2010. С. 34-39.

2 Алексеева Л.А., Украинец В.Н. Динамика упругого полупространства с подкрепленной цилиндрической полостью при подвижных нагрузках //Прикладная механика, 2009. Т. 45. №.9. С. 75-85.

3 Ержанов Ж.С., Айталиев Ш.М., Алексеева Л.А. Динамика тоннелей и подземных трубопроводов. Алма-Ата, 1989. – 240 с.