Шалкаров А.А.

Казахский университет путей сообщения, г Алматы, РК.

ПРОГИБ МОСТОВЫХ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ

Расчет прогиба железобетонных конструкций относится к расчетам второй группы предельных состояний. Ее цель – обеспечить условия нормальной эксплуатации конструкций.

В настоящее время деформации элементов железобетонных конструкций определяются по кривизнам, используя формулы сопротивлении материалов. В предварительно-напряженных конструкциях кривизны и деформации отсчитывают от состояния до обжатия. Кривизна предварительно напряженных элементов, согласно [1] определяется по формуле (136)

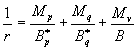(1)

Кроме того усилия предварительного обжатия, усадка и ползучесть бетона влияют на выгиб конструкций, величина которого играет немалое значение для определения деформативности конструкций.

При серийном испытании балочных плит к.т.н., доцентом Боровиковым А.И. выявлен эффект «хлопка». В результате проведения сравнительных экспериментов с балками пролетных строений, в которых напрягаемая арматура в одном случае располагалось полностью прямолинейно (ортогонально) к оси конструкции, а в другом – полигонально с одним узлом перегиба в середине пролета, установлено, что в конструкциях с прямолинейным расположением арматуры при исчерпании выгиба происходит пластичный «хлопок», т.е. предварительно напряженная конструкция прогибается без увеличения нагрузки до появления трещин в растянутой зоне [2].

При этом установлено, что хлопок происходит при переходе от выгиба под постоянной нагрузкой пластично. Хлопок бывает только у балок с прямолинейным расположением арматуры при загружении парой сил. Также установлено, что чем больше плечо пары сил, тем хлопок больше. Под равномерно распределенной нагрузкой балки не испытывалось, но было замечено, что балки, у которых прогиб под собственным весом близок к расчетной величине выгиба от обжатия, имеют начальный прогиб, равный по величине хлопку, определенному расчетным путем.

При приложении пары сил с плечом создается заранее фиксированный участок, на котором сила обжатия от противодействия поперечной силе начинает увеличивать прогиб на коэффициент . Происходит это скачком от импульса поперечной силы на незначительную величину .

Положение неустойчивого равновесия образуется тогда, когда внешний момент равен моменту обжатия:

(2)

и переходит в устойчивое состояние при:

(3)

В положении, когда в балке накоплена потенциальная энергия:

(4)

Уравнения (4) при характеризуют состояние неустойчивого равновесия. Следовательно силы уравновесили друг друга, конструкция находится в состоянии покоя, но достаточно незначительного импульса силы, чтобы система пришла в движение. Положение неустойчивого равновесия.

При прямоугольной эпюре напряжений накоплена потенциальная энергия

(5)

При придании поперечной силе импульса происходит частичное освобождение энергии в нижней зоне сечения, равное моменту:

(6)

Этот момент сложится с внешним моментом, а т.к. тогда:

(7)

Таким образом произойдет увеличение работы без увеличения внешней силы и силы обжатия за счет освобождения энергии сжатия в растянутой зоне на участке плеча пары сил .

Следует также отметить, что когда эпюра напряжений бетона имеет прямоугольную форму (см.рис.1-б):

(8)

Когда напряжение обжатия на растянутой грани , тогда , следовательно будет равенство:

(9)

Таким образом внутренняя потенциальная энергия не исчезает и не увеличивается, т.е. работа, проделанная на деформациях обжатия сохраняется постоянно. Работа проделанная силой обжатия до уравновешивания ее работой внешних сил, препятствует прогибу балки, а когда внешний момент превышает момент обжатия, происходит обратное явление.

Таким образом величина хлопка равна величине прогибов от момента:

(10)

Для балки пролетом 18м.:

Это примерно 18% от допустимого прогиба по проекту, который равен

Полный прогиб с учетом хлопка будет равен:

(11)

Следует отметить, что эта формула универсальна для всех видов загружения на участке работы балки до начала микроразрушений перед образованием трещин. Разница только в том, что при приложении пары сил с плечом освобождение энергии сжатия происходит хлопком, а при других видах загружения хлопок накладывается на график прогибов постепенно с увеличением от 0 до .

Как при сосредоточенной силе в середине пролета, так при равномерно распределенной нагрузке расстояние от сечений, где растет (рис.1) и доля прогиба от равна:

(12)

Необходимо вводить в расчет на всех этапах определения прогиба дополнительный член (12). Но следует отметить, что при расположении напрягаемой арматуры под углом с узлом перегиба в середине пролета хлопка не бывает и жесткость балки в целом увеличивается.

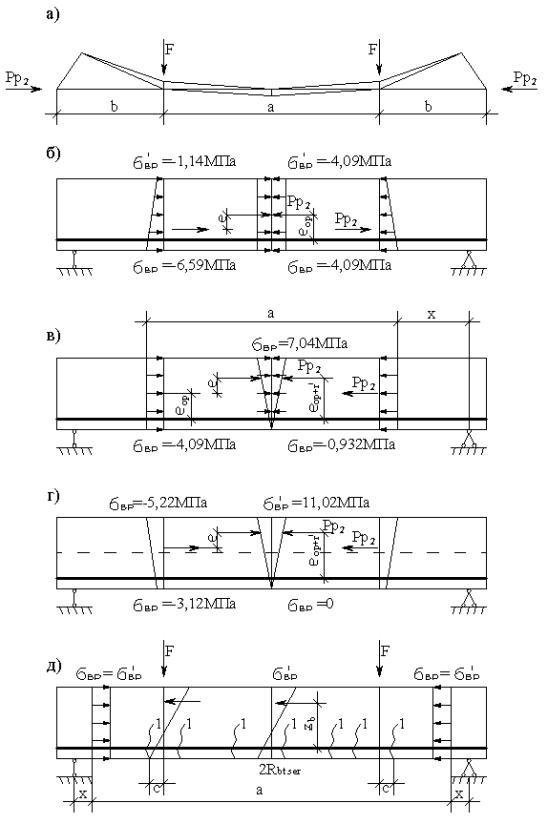
Рис. 1. Физический смысл явления "хлопка"

а) суммарная эпюра моментов ;

б) начало хлопка;

в) середина хлопка;

г) конец хлопка;

д) схема образования первых трещин.

При определении необходимо определять плечо пары сил или расстояние между сечениями, когда (рис.1) и когда . Тогда определяется из уравнений (15) и (16) при определении :

- для равномерно распределенной нагрузки:

(13)

В сочетании нескольких сосредоточенных сил и распределенной нагрузки:

(14)

Решая квадратное уравнение при известном , определим расстояние , которое определяется для симметричной нагрузки по формуле:

(15)

При несимметричном расположении нагрузки следует определять от левой и от правой опоры по формуле:

(16)

Литература

1. СНиП 2.05.03-84* Мосты и трубы / Минстрой России. – М.: ГП ЦПП, 1996. – 214 с.

2. Боровиков А.И., Мамлютов Т.Х., Лавриненко В.П. Понигональное расположение напряженной арматуры – резерв экономии стали // Строительные материалы и изделия, № 8. – Алма-Ата, 1988. – 16 с.