Тулешов А.К., Таирова Ф.Л.

ИММаш им.У.А.Джолдасбекова, Алматы, Казахстан

ДЕКОМПОЗИЦИОННЫЙ ПОДХОД К ИССЛЕДОВАНИЮ УСТОЙЧИВОСТИ ДВИЖЕНИЯ СЛОЖНОЙ ЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЫ

Движение широкого класса машин с многодвигательным электро- приводом, примером которой являются многократный волочильный стан, роботы-манипуляторы, системы координатно-параметрического управления, многие другие типы непрерывно-поточных машин-агрегатов[2] описываются системой нелинейных дифференциальных уравнений, в которой одна подсистема содержит все переменные системы, а другая - лишь часть переменных[1,2]. Особенностью данного класса электромеханических систем является большая размерность вектора переменных и наличие нелинейных элементов с характеристиками, задаваемыми графически. Непосредственное применение метода Ляпунова к исследованию устойчивости положения равновесия таких систем приводит к громоздким и неудобным для инженерного анализа условиям, определяющим лишь область устойчивости "в малом"[3,4]. В этом пункте работы предлагается декомпозиционный подход[2], позволяющий получить достаточно простой критерий асимптотической устойчивости исследуемой системы при любых начальных условиях из области определения уравнений движения на основе критериев устойчивости двух ее подсистем, одна из которых является линейной.

Рассмотрим электромеханическую систему, описываемую уравнениями вида:

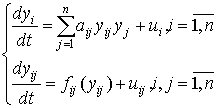(1)

где - вектор переменных состояния, включающий векторы фазовых координат механической подсистемы и электропривода ;

- вектор управления, включающий управляемые переменные механической системы и электропривода , удовлетворяющих условиям:

(2)

- матрица постоянных параметров механической системы;

- непрерывно-дифференцируемые монотонно-убывающие функции определенные в области

(3)

Требуется найти область асимптотической устойчивости

положения равновесия системы (1) соответствующего заданному

значению вектора управления из области

(4)

где

- достаточно мало.

В матричной форме система уравнений (1) имеет вид:

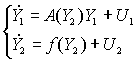
где - матрица элементов

- вектор-функция от .

Положение равновесия системы (5) определяется как

решение системы алгебраических уравнений:

(6)

Второе уравнение системы (6) разрешимо однозначно относительно в силу непрерывности, монотонности и взаимной независимости компонент вектор - функции.

(7)

причем с учетом условий (3), (4)

Подставляя решение (7) в первое уравнение, получим:

Если матрица - неособая, то положение равновесия системы (4.5) определяется равенствами

(8)

Выведем уравнения движения системы (5) в отклонениях от положения ее равновесия (8), приняв его за невозмущенное движение системы и положив

Тогда уравнение (5) с учетом (8) примет вид:

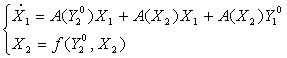
где - с областью определения

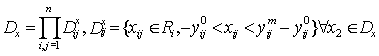
Пусть - какое-либо ненулевое решение этого уравнения. Подставляя указанное решение в первое уравнение системы (9), придем к линейному неоднородному уравнению с переменными коэффициентами:

(10)

где матрица с постоянными элементами

-матрица с непрерывно-зависящими от

времени элементами

Очевидно, для асимптотической устойчивости ненулевого решения системы (9) необходимо и достаточно, чтобы были асимптотически устойчивыми нулевые решения обоих уравнений системы и выполнены условия для евклидовых норм

(11)

(12)

Известно [1], что для асимптотической устойчивости линейной неоднородной системы (10) при любом свободном члене в свою очередь, необходимо и достаточно, чтобы была асимптотически устойчивой соответствующая однородная система

(13)

Кроме того, выполнение условия (11) возможно очевидно лишь тогда, когда частное решение , системы (10), соответствующее свободному члену удовлетворяет условию

(14)

Рассмотрим частное решение неоднородной системы (10), которое определяется как

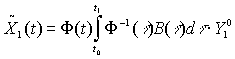(15)

где - фундаментальная матрица системы (13).

Заметим, что для выполнения условия (14) достаточно, чтобы:

при (16)

Рассмотрим теперь устойчивость однородной системы (13), которую можно рассматривать как возмущенную по отношению к системе с постоянной матрицей

(17)

Согласно [1] из асимптотической устойчивости положения равновесия системы (17), т.е. следует асимптотическая устойчивость возмущенной системы (13), если выполнено условие (16). Остается удовлетворить условиям, при которых система (13) и (17) асимптотически эквивалентны, т.е. между решениями и можно установить соответствие

Эти условия согласно [1,2] заключаются в абсолютной

интегрируемости на , т.е.

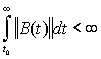
Следует заметить, что условие (18) является достаточным для выполнения условия (16).

Исследуем устойчивость положения равновесия второй системы и найдем условия, при которых выполняется соотношение (12), а в силу определения матрицы и условие (16).

Предположим, что функция удовлетворяет условиям

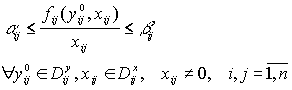
Тогда нетрудно показать, что

(19)

откуда следует, что для выполнения условия (12) достаточно, чтобы ,

При этом выполняется и условие (18), т.к. имеет место экспоненциальная устойчивость решений (19) и при любых начальных условиях решения для любого т.е. бесконечно продолжаемы вправо. Последнее имеет место и для любого решения первой подсистемы в силу ее линейности и непрерывности матрицы , следовательно, областью притяжения нулевого решения системы (1) является вся область

Таким образом, справедлива теорема 1: Положение равновесия системы (1)-(3) определяемое уравнениями (6) асимптотически устойчиво при любых начальных условиях, если все характеристические корни матрицы лежат в левой полуплоскости

и нелинейные функции удовлетворяют условиям

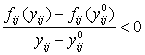
при любых

Практическое значение доказанное теоремы заключается в том[2], что она позволяет ответить на вопрос об устойчивости сложной электромеханической нелинейной системы по устойчивости ее линейной части и по характеристикам нелинейных элементов. При известных характеристиках нелинейных элементов оценка устойчивости линейной стационарной системы является обычной инженерной задачей.

Литература

1. Демидович Б.П. Лекции по математической теории устойчивости - М.: Наука, 1967.

2. Джолдасбеков У.А., Молдабеков М.М., Тулешов А.К. Стабилизация натяжения проволоки в многократных прямоточных волочильных станах. Монография, ISBN - 9965 – 408 - 04 - 01. -Алматы, 1998. -127 с.

3. Малкин И.Г. Теория устойчивости движения - М.: Гостехиздат, 1967.

4. Барбашин Е.А. Функиции Ляпунова. - М.: Наука, 1970.