Физика /1.Теоретическая физика

К.п.н. Мищик С.А.

Государственный морской университет имени адмирала Ф.Ф.Ушакова ,

Россия

Системные акустические задачи прикладной физики

морского флота

Системные акустические задачи прикладной физики морского флота отражают целостно-системное моделирование основных элементов транспортных объектов. При этом возникает ориентация на единство базисных характеристик предметных и исполнительных условий относительно предмета содержания и способа его реализации. Рассматриваются: общие вопросы акустики; линейная акустика идеальной среды; затухание звука в жидкостях и газах; релаксационное поглощение; отражение и преломление звука; отражение от слоя и прохождение через слой; движение и звук на морском флоте.

В процессе решения системных задач акустической прикладной физики морского флота необходимо применять основные положения теории деятельности, системного анализа и теории формирования интеллекта.

Системный анализ предполагает выполнение последовательности системных аналитических действий: выделить объект анализа – акустическую задачу прикладной физики морского флота (АЗПФМФ) как систему; установить порождающую среду АЗПФМФ; определить уровни анализа АЗПФМФ; представить целостные свойства АЗПФМФ относительно пространственных, и временных характеристик и их комбинаций; выделить структуру уровня анализа АЗПФМФ; установить структурные элементы уровня анализа АЗПФМФ; определить системообразующие связи данного уровня анализа АЗПФМФ; представить межуровневые связи анализа АЗПФМФ; выделить форму организации АЗПФМФ; установить системные свойства и поведение АЗПФМФ.

Задача 1

Пуля пролетела со скоростью 660 м/с на расстоянии 5 м от морского пехотинца. На каком расстоянии от морского пехотинца была пуля, когда он услышал ее свист? Скорость звука 332 м/с.

Ответ: 9,6 м

Задача 2

Эхолот измеряет глубину моря по отражению звука от морского дна. Какова должна быть минимальная точность в определении времени отправления и возврата сигнала, если прибор рассчитывается на измерение глубин более 30 м с точностью до 5%? Скорость звука в воде 1500 м/с.

Ответ: 10^-3 c

Задача 3

Узкий пучок ультразвуковых волн частотой ν₀ = 5O кГц направлен от неподвижного локатора к приближающейся подводной лодке. Определить скорость U подводной лодки, если частота ν₁ биений (разность частот колебаний источника и сигнала, отраженного от лодки) равна 250 Гц. Скорость υ ультразвука в морской воде принять равной 1,5 км/с.

Ответ:

Задача 4

Приближающийся теплоход дал гудок, звук которого услышали на мосту через 3 с. Спустя 3 мин теплоход прошёл под мостом. Температура воздуха 0⁰ С. Найти скорость движения парохода. Скорость звука 332 м/с.

Ответ: 6 м/с .

Задача 5

Сигнальная ракета, запущенная вертикально вверх с палубы судна, разорвалась через 5,0 с после запуска, а звук разрыва был услышан через 0,4 с после разрыва. На какую высоту и с какой средней скоростью поднялась ракета? Температура воздуха 0⁰ С. Скорость звука 332 м/с.

Ответ: 130 м; 26 м/с.

Задача 6

Определить глубину моря в точке обсервации судна, если ультразвук судовой акустической системы был принят через 0,9 с? Скорость ультразвука в воде 1555,5 м/с.

Ответ: 700 м.

Задача 7

Судовую гидроакустическую установку применили для измерения скорости потока воды в морской узкости. Определить скорость течения в узкости, если расстояние между вибраторами 100 метров ультразвук проходит в одном направлении за 0,5 с, а в противоположном – за 1,0 с.

Ответ: 50 м/с.

Задача 8

Из судового орудия произвели выстрел под углом 26⁰ к горизонту. Орудийный расчёт услышал разрыв снаряда через 44 с после выстрела. Определить горизонтальную дальность полёта снаряда, если его начальная скорость 800 м/с.

Ответ: 10 км.

Задача 9

Самолёт пролетел со скоростью 500 м/с на расстоянии 6 км от морского судна. На каком расстоянии от корабля был самолёт, когда служба наблюдения приняло его звук. Скорость звука 332 м/с.

Ответ: 9 км.

Задача 10

Амплитуда колебаний давления звуковой волны в судовом машинном отделении достигает 0,001 Н/см² . Найти поток энергии, попадающей за 1 с в ухо вахтненному механику. Считать площадь уха 4 см² и ухо распологается перпендикулярно направлению распространения волны. Плотность воздуха 1,3 кг/м³ . Скорость звука 332 м/с.

Ответ: 4,6·10^-5 Вт.

Задача 11

Интенсивность звука в морской воде согласно эмпирической формуле убывает вследствие поглощения на величину , где f — частота в килоГерцах. Определить, на каком расстоянии r от источника затухание уменьшит амплитуду волны в 100 раз при частотах 10 и 100 кГц.

Ответ: r₁= 35км; r₂ = 1,1км.

Задача 12

Найти переходное расстояние, на котором в сферической волне потери энергии на расхождение равны потерям на поглощение. Вычислить это расстояние в пресной воде при температуре 14⁰С на уровне моря, когда коэффициент вязкости равен 1,14·10^-3 Па·с. Частота звука 10 кГц.

Ответ: 1 км.

Задача 13

Найти коэффициент отражения по давлению и коэффициент передачи энергии при нормальном падении звука из воздуха в воду и из воды в воздух. Плотность воздуха ρ₁ = 1,29 кг/м³, воды ρ₂ = 10³ кг/м³. Скорость звука соответственно с₁ = 340 м/с, с₂ = 1480 м/с. Как изменится коэффициент передачи при косом падении волны на границу раздела сред?

Ответ: V_p = - 0,9994; W_J = 0,0012 .

Задача 14

Ультразвуковой магнитострикционный никелевый преобразователь судовой акустической системы помещен в морскую воду. Какая доля энергии акустической волны, распространяющейся в никеле, при этом передается морской воде? Плотность никеля ρ₁ = 8·10³ кг/м³; скорость звука в нём с₁ = 5·10³ м/с. Плотность морской воды ρ₂ = 1030 кг/м³, скорость звука в ней с₂ = 1480 м/с. Считать для оценок, что задача сводится к нормальному падению плоской волны на границу.

Ответ: W_J = 0,13.

Задача 15

Вычислить коэффициент отражения звука, падающего под малыми углами скольжения из воды на морской грунт, который рассматривается как жидкая среда с потерями. Плотность морской воды ρ₁ = 1030 кг/м³, скорость звука в ней с₁ = 1480 м/с. Плотность жидкого грунта ρ₂ = 2200 кг/м³, комплексная скорость звука в грунте , где c₀₂ = 1500 м/с, угол потерь δ считается не зависящим от частоты (δ = 0,01) .

Ответ: V_P =.

Задача 16

Во сколько раз уменьшается мощность плоской звуковой волны с частотой f =1 кГц при прохождении через стальную судовую переборку толщиной 2,5 см, которая разделяет два отсека подводной лодки заполненные водой. Плотность стали 7,8 г/см³ , скорость звука в ней 5100 м/с.

Ответ: 0,01.

Задача 17

Теплоход плывет параллельно берегу моря со скоростью v = 20 км/ч и подает гудки на частоте f₀ = 200 Гц. На какой частоте звук принимает водитель автомобиля, движущегося параллельно берегу со скоростью u = 80 км/ч, если звуковой луч образует с направлениями движения угол θ ? Рассмотреть случаи θ = 60⁰, 90⁰, 120°.

Ответ: 182 Гц; 200 Гц; 233 Гц.

Задача 18

Звуковой сигнал парохода падает под углом θ = 45⁰ на границу атмосферного ветра, движущегося со скоростью u₀ = 10 м/с. Вычислить коэффициенты отражения и прозрачности.

Ответ: V=0,002; W = 1.

Задача 19

Пароход посылает гудки об опасности в направлении ветра, скорость которого v. Эхо сигнала отражается от прибрежных гор, удаленных на расстоянии ℓ, и принимается на пароходе. Через какое время будет принят отраженный сигнал?

Ответ: .

Задача 20

Низкочастотный звук судовой турбины распространяется вдоль оси х цилиндрической трубки системы автоматического правления с площадью поперечного сечения S. Звуковое поле воздействует на колебательную систему, состоящую из поршня массой m и пружинки с жесткостью k . Трение пропорционально скорости поршня (F_тр = - ах), где х — смещение из положения равновесия. Определить, при каких условиях возможно полное поглощение звуковой волны, падающей на поршень системы автоматического управления.

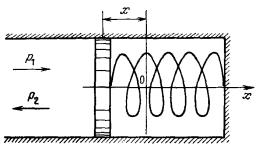
Ответ: .

Задача 21

Определить коэффициент прохождения звукового хлопка в судовом трубопроводе (по энергии) при переходе из трубы сечением 10 см² в трубу сечением 7 см².

Ответ: W_J = 0,97.

Задача 22

В сторону берегового шельфа, каменистое дно которого образует с горизонтальным уровнем воды угол 1,1°, распространяется звук с частотой 6 кГц от ненаправленного судового излучателя. Определить число незатухающих мод, приходящих в точки, расположенные на расстояниях 10 и 50 м от берега. Найти углы наклона к горизонту лучей Бриллюэна на расстоянии 10 м от берега. Скорость звука в воде 1480 м/с.

Ответ: на расстоянии 10 м образуются две незатухающие моды;

при 50м—восемь мод. Углы наклона лучей Бриллюэна при 18,7° и 41,7°.

Задача 23

При распространении звука в океане вертикальное отклонение луча z во много меньше размера неоднородности H. Используя это условие, получить из формулы явное выражение z = z (х) для траектории луча.

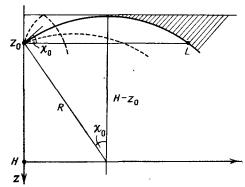
Ответ: . Луч представляет собой параболу.

Задача 24

При определении скорости звука часто используют различные эмпирические формулы, которые позволяют по измерениям температуры t (в градусах Цельсия), солености s (в промиллях; 1 %₀ = 0.1 %), глубины z (в метрах); рассчитать скорость звука с (в м/с). Формулы различаются точности оп- ределения скорости. Одной из них является формула

Она обеспечивает точность до 1 м/с в диапазоне температур t от 0 до 35 °С, солености s от 0 до 45 %₀, глубины z 0 до 1000 м. Пусть судно находится в широком устье реки, несущей пресную воду в море. Верхние 5м—это пресная вода при температуре 20⁰С. Ниже находится толща морской воды с соленостью

20 %₀ и температурой 15°С. Максимальная глубина Н = 20 м. Найти и построить профиль скорости звука. Необходимо ли учитывать добавку к скорости звука, связанную гидростатическим давлением, последнее слагаемое уравнения? Найти коэффициент отражения по давлению V от скачка скорости.

Ответ: 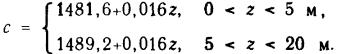Поправка, связанная с гидростатическим давлением, меньше точности формулы. Коэффициент отражения равен V = 2,5·10^-3.

Задача 25

Гидролокатор лоцирует объект, находящийся под слоем резкого отрицательного скачка скорости звука (под термоклином). Найти ослабление принимаемого сигнала К, связанное с наличием термоклина.

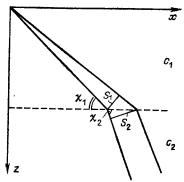
Ответ: К= .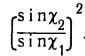

Задача 26

Найти ослабление силы звука при эхолоцировании с поверхности подводного объекта, находящегося непосредственно под термоклином, с перепадом скорости Δс = 50 м/с (с₁ = 1450 м/с), если расстояние до объекта r = 1 км, а термоклин расположен на глубине h = 100 м. Ответ: .

Задача 27

Определить полную мощность излучения звука судовой сигнальной системой в виде сферы радиусом 1 см, совершающей в воздухе поступательные колебания на частоте f = 100 Гц с амплитудой смещения = 1 мм. Как изменится мощность, если колебания происходят в воде?

Ответ: ; для воды излучаемая мощность в 10 раз выше.

Задача 28

Вахтенный гидроакустик неподвижной подводной лодки воспринимает звуковые колебания от двух подводных лодок, одна из которых приближается, а другая - с такой же скоростью удаляется. При этом гидроакустик слышит биения с частотой Δv. Найти скорость каждой подводной лодки, если звуковая частота их колебаний v_о, а скорость звука u .

Ответ: .

Задача 29

Оценить радиус первой зоны Френеля на дне океана для гидролокатора, работающего на частоте f = 45 кГц при глубине места h = 3200 м. Скорость звука принять равной 1500 м/с. Ответ: r₁ = 10 м.

Задача 30

Наблюдатель на берегу моря слышит звук пароходного гудка. Когда наблюдатель и пароход находятся в покое, частота воспринимаемого наблюдателем звука v=420 Гц. При движении парохода воспринимаемая частота v₁=430 Гц, если пароход приближается к наблюдателю, и v₂=415 Гц, если пароход удаляется от него. Найти скорость v парохода в первом и во втором случаях, если скорость распространения звука в воздухе с=338 м/с.

Ответ: v₁ = 28,3 км/ч; v₂ = 14,7 км/ч.

Литература:

Акустика в задачах. Под ред. С.Н.Гурбатова и О.В.Руденко.—М.: Наука. Физматлит, 1996.—336 с.