Ш.А. БАЛГИМБАЕВА
Институт Математики, г.
Алматы
ОЦЕНКИ ВОССТАНОВЛЕНИЯ
ОПЕРАТОРА ДИФФЕРЕНЦИРОВАНИЯ ПО ИНФОРМАЦИИ О СПЕКТРЕ
Напомним общую
постановку задачи восстановления. Пусть ![]() - некоторое множество
в векторном пространстве
- некоторое множество
в векторном пространстве ![]() . Про каждый элемент
. Про каждый элемент ![]() мы располагаем
информацией
мы располагаем
информацией ![]() , где
, где ![]() - (однозначное)отображение (называемое информационным) из
- (однозначное)отображение (называемое информационным) из ![]() в другое векторное
пространство
в другое векторное
пространство ![]() . Информация об элементах из
. Информация об элементах из ![]() может быть задана
неточно, и потому
может быть задана
неточно, и потому ![]() , вообще говоря, - многозначное отображение. Пусть, далее
, вообще говоря, - многозначное отображение. Пусть, далее ![]() - нормированное
пространство и
- нормированное
пространство и ![]() - линейный оператор.
- линейный оператор.
Задача заключается в
том, чтобы восстановить по возможности наилучшим образом оператор ![]() на классе
на классе ![]() в метрике
пространства
в метрике
пространства ![]() по имеющейся информации
по имеющейся информации
![]() . Любое отображение
. Любое отображение ![]() будем называть
методом восстановления. Погрешностью этого метода называется величина
будем называть
методом восстановления. Погрешностью этого метода называется величина
![]() .
.
Задаче о приближении (вообще говоря
неограниченного) оператора ограниченными линейными операторами на классах
функций (задаче Стечкина С.Б. ) и
родственным экстремальным задачам посвящено много работ. Отметим лишь, что
ранее подробно исследовано наилучшее приближение операторов, инвариантных
относительно сдвига в пространствах ![]() . Оператор дифференцирования
также является инвариантным относительно
сдвига.
. Оператор дифференцирования
также является инвариантным относительно
сдвига.
Введем некоторые
обозначения. Пусть ![]() - множества
натуральных, целых, вещественных чисел соответственно;
- множества
натуральных, целых, вещественных чисел соответственно; ![]() - множество всех неотрицательных целых чисел,
- множество всех неотрицательных целых чисел, ![]() - n-мерное евклидово
пространство. Для
- n-мерное евклидово
пространство. Для ![]() ,
, ![]() , как обычно,
, как обычно, ![]() - скалярное произведение. Для мультииндекса
- скалярное произведение. Для мультииндекса ![]() через
через ![]() обозначим его длину. Обозначим
обозначим его длину. Обозначим 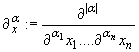 .
.
Запись ![]() означает, что
существуют константы
означает, что
существуют константы ![]()
![]() .
.
Пусть ![]() - пространства Шварца
всех бесконечно дифференцируемых быстроубывающих комплекснозначных функций и медленно растущих распределений (обобщенных
функций) на
- пространства Шварца
всех бесконечно дифференцируемых быстроубывающих комплекснозначных функций и медленно растущих распределений (обобщенных
функций) на ![]() соответственно,
соответственно, ![]() - пространство бесконечно дифференцируемых функций
с компактным носителем в
- пространство бесконечно дифференцируемых функций
с компактным носителем в ![]() .
.
Преобразование Фурье
обобщенной функции ![]() обозначим через
обозначим через ![]() . В частности, если
. В частности, если ![]() , то
, то
![]() .
.
Известно, что ![]() представляет собой изоморфизм
представляет собой изоморфизм ![]() и
и![]() на себя.
на себя.
Обратное преобразование
Фурье обозначим через ![]() .
.
Для ![]() рассмотрим сужение
рассмотрим сужение ![]() на
на ![]() как сужение обобщенной
функции, т.е. как линейный непрерывный
функционал над пространством
как сужение обобщенной
функции, т.е. как линейный непрерывный
функционал над пространством ![]() .Обозначим данное сужение через
.Обозначим данное сужение через ![]() .
.
Определение 1.
Пусть ![]() . Тогда как обычно
имеем
. Тогда как обычно
имеем
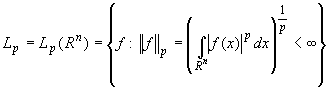 .
.
Определим пространства
Никольского - Бесова ![]() (см., например, [1, 2]).
(см., например, [1, 2]).
Определение 2. Функция ![]() принадлежит пространству
принадлежит пространству ![]() ,
, ![]()
![]() , если
, если ![]() и для нее конечна полунорма (
и для нее конечна полунорма (![]() )
)
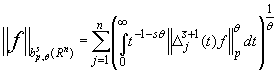 .
.
При этом полагаем ![]() .
.
Здесь ![]() - оператор m-й разности по
- оператор m-й разности по ![]() -й переменной.
-й переменной.
Нами рассматривается задача
восстановления оператора дифференцирования
![]() в пространстве Никольского – Бесова
в пространстве Никольского – Бесова ![]() .
.
В качестве информации о
функциях ![]() используется сужение преобразования Фурье
используется сужение преобразования Фурье ![]() . Таким образом, предполагаются известными значения функционала
. Таким образом, предполагаются известными значения функционала ![]() на любых функциях из
на любых функциях из ![]() .
.
Отметим, что задача
оптимального восстановления операторов на функциональных классах на основе информации
о спектре рассматривалась в [3]. А именно, рассматривается задача оптимального восстановления
функций и их производных по информации о
спектре
Известно, что для любой
обобщенной функции ![]() ее разложение в ряд
Фурье по всплескам Мейера сходится к
ее разложение в ряд
Фурье по всплескам Мейера сходится к ![]() в топологии
в топологии ![]() .
.
В качестве (линейного)
метода приближенного восстановления оператора ![]()
![]() , использующего информацию
, использующего информацию ![]() о функции
о функции ![]() , будем рассматривать
специальную «частную» сумму ее
разложения в ряд по всплескам Мейера.
, будем рассматривать
специальную «частную» сумму ее
разложения в ряд по всплескам Мейера.
Сформулируем некоторые
известные факты, которые использованы в
работе.
1. Как известно ([1],
стр. 295), функция
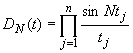
называется
ядром Дирихле порядка ![]() в n-мерном
непериодическом случае.
в n-мерном
непериодическом случае.
Ее преобразование Фурье
имеет вид
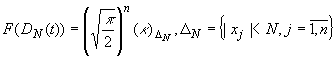 .
.
Отметим, что ![]() обладает следующими
свойствами, которые будут использованы ниже.
обладает следующими
свойствами, которые будут использованы ниже.
1) ![]() - целая функция
экспоненциального типа
- целая функция
экспоненциального типа ![]() по каждой переменной
по каждой переменной ![]() , принадлежит
, принадлежит ![]() .
.
2) Свертка
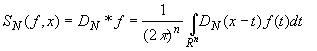
для ![]() есть целая функция
экспоненциального типа
есть целая функция
экспоненциального типа ![]() по каждой переменной
и принадлежит
по каждой переменной
и принадлежит ![]() .
.
При этом
![]() ,
,
где ![]() зависит только от
зависит только от ![]() и от
и от ![]() .
.
3) ![]() слабо при
слабо при ![]() .
.
Тогда регулярную в
смысле ![]() функцию
функцию ![]() можно разложить в
(слабо сходящийся) ряд
можно разложить в
(слабо сходящийся) ряд
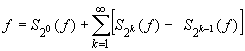 .
.
Верна теорема (см. [1])
Теорема А. Пусть ![]() - произвольное
действительное число.
- произвольное
действительное число.
![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]() регулярна в смысле
регулярна в смысле ![]() и ее (сходящийся к ней слабо) ряд
и ее (сходящийся к ней слабо) ряд
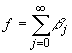 ,
,
где ![]() ,
таков, что
,
таков, что
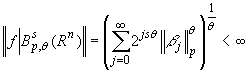 .
.
(с естественной метрикой при ![]() .)
.)
2. Определим кратную
систему одномерных всплесков Мейера (см., например, [4] или [5]).
Пусть ![]() - нечетная бесконечно
дифференцируемая функция
- нечетная бесконечно
дифференцируемая функция
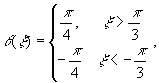
![]() - четная функция,
такая что
- четная функция,
такая что
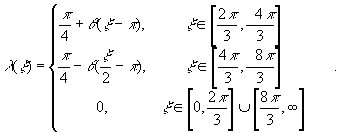
Преобразование Фурье масштабной
функции Мейера ![]() определяется как
определяется как
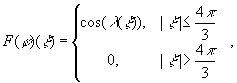
откуда
![]() .
.
Тогда
![]() .
.
С помощью операций
сдвига и растяжения определяем функции
![]() .
.
Из определения видно,
что
![]() .
.
Ясно также, что всплески
Мейера – это целые функции экспоненциального типа, принадлежащие ![]() .
.
Теперь введем ![]() -мерную систему всплесков Мейера
-мерную систему всплесков Мейера ![]()
![]() следующим образом:
следующим образом:
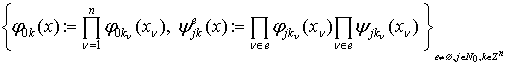 ;
;
здесь ![]() пробегает все непустые
подмножества множества
пробегает все непустые
подмножества множества ![]() ,
, ![]()
![]() .
Известно, что система всплесков
.
Известно, что система всплесков ![]() образует
безусловный базис в пространстве
образует
безусловный базис в пространстве ![]() (см., например, [5]).
(см., например, [5]).
Верна теорема (см. [6])
Теорема В . Для любой ![]() ограниченной целой
функции экспоненциального типа
ограниченной целой
функции экспоненциального типа ![]() справедливо
соотношение
справедливо
соотношение ![]() .
.
Здесь ![]() - проекционный оператор
на подпространство
- проекционный оператор
на подпространство ![]() .
.
В качестве метода
приближенного восстановления оператора ![]() рассмотрим следующий
оператор
рассмотрим следующий
оператор ![]() :
:
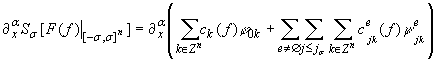 ,
,
где
![]()
- коэффициенты Фурье ![]() по системе
по системе ![]() , а
, а ![]() .
.
По
формуле Планшереля для любых ![]() :
:
![]() .
.
Из определения следует, что ![]() ; ясно также, что
; ясно также, что
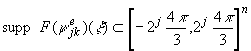 ,
,
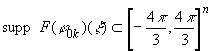 .
.
Таким образом, метод ![]() использует
информацию только о
использует
информацию только о ![]() .
.
Основной результат настоящей статьи содержится в
следующей теореме.
Теорема. Пусть ![]() ,
, ![]() ,
,
![]() , причем
, причем
![]() ,
где
,
где ![]() ,
, ![]() - мультииндекс. Тогда для
метода восстановления
- мультииндекс. Тогда для
метода восстановления ![]() справедливы оценки:
справедливы оценки:
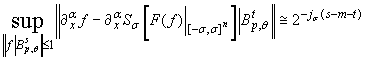
Доказательство.
Приведем схему получения оценки сверху. Выше
через ![]()
мы обозначили действие оператора
дифференцирования на специальную «частную» сумму разложения в ряд по всплескам Мейера. Далее, для краткости будем
обозначать ![]() . Тогда имеем
. Тогда имеем
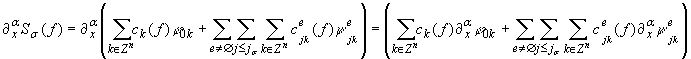
Рассмотрим норму разности ![]() , где
, где ![]() - банахово пространство.
Используя линейность операторов
- банахово пространство.
Используя линейность операторов ![]() и применяя теорему B
для
и применяя теорему B
для ![]() - целой
функции экспоненциального типа
- целой
функции экспоненциального типа ![]() , на которой реализуется
наилучшее приближение функции
, на которой реализуется
наилучшее приближение функции ![]() , получим:
, получим:
![]()
Пусть ![]() .
Функция
.
Функция ![]() , следовательно по теореме А справедливо представление
, следовательно по теореме А справедливо представление ![]() .
Очевидно, что
.
Очевидно, что ![]() , где
, где ![]() . Теперь, используя эквивалентную
нормировку, приведенную в теореме А и
неравенство Бернштейна, получим оценку
. Теперь, используя эквивалентную
нормировку, приведенную в теореме А и
неравенство Бернштейна, получим оценку
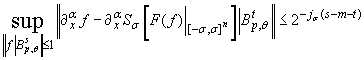 .
.
Таким образом, оценка сверху получена.
При получении оценок снизу строятся
"плохие" функции из
единичного шара пространства ![]() ,
на которых реализуется порядок, комбинированием
теоремы представления A и теоремы B.
,
на которых реализуется порядок, комбинированием
теоремы представления A и теоремы B.
ЛИТЕРАТУРА
1.
Никольский
С.М. Приближение функций многих переменных и теоремы вложения. М.,Наука., 1997.
456с.
2.
Трибель
Х. Теория функциональных пространств. М., Мир., 1986. 448с.
3.
Магарил-Ильяев
Г.Г., Осипенко К.Ю. Оптимальное восстановление функций и их производных по
приближенной информации о спектре и неравенства для производных// Функциональный
анализ и его приложения. 2003. Т.37. вып.3. с.51-64.
4.
Meyer Y. Wavelets and operators.
Cambridge
Univ. Press, 1992.
5.
Стечкин
С.Б., Новиков И.Я. Основы теории
всплесков// Успехи мат. наук. 1998. Т.53. вып.6(324). с. 54-128.
6. Новиков И.Я. Онделетты
И.Мейера – оптимальный базис в ![]() //
Мат. заметки. 1992. Т.52. вып.5. с. 88-92.
//
Мат. заметки. 1992. Т.52. вып.5. с. 88-92.