1.Дифференциальные
и интегральные уравнения
Ж.Б. Муканов
Евразийский национальный университет им. Л.Н.Гумилева,
г.Астана
ОБ ОДНОМ УСЛОВИИ ИНТЕГРИРУЕМОСТИ
КОСИНУС ПРЕОБРАЗОВАНИЯ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ.
В работе рассматриваются вопросы интегрируемости двойного косинус
преобразования.
Напомним,
что двойное косинус преобразование для функции ![]() определяется
равенством
определяется
равенством
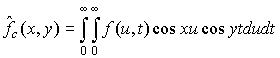
Далее приводится достаточное условие интегрируемости двойного косинус-преобразования Фурье и справедливости формулы
обращения.
Для функции
одной переменной ![]() известно, что если
известно, что если ![]() и её
косинус–преобразование
и её
косинус–преобразование
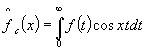
также принадлежит ![]() , то имеет место формула обращения
, то имеет место формула обращения
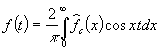 .
.
Но
косинус–преобразование может быть неинтегрируемой функцией. Например,
косинус-преобразование характеристической функции отрезка [0,1] не является
интегрируемой.
Известна
следующая теорема, доказанная Dang Vu Gians и Ferenc Moricz [1].
Теорема А. Пусть
![]() абсолютно непрерывная
функция, определенная на
абсолютно непрерывная
функция, определенная на ![]() ,
, ![]() , и пусть для некоторого
, и пусть для некоторого ![]() выполняется условие
выполняется условие
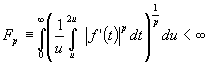 . (1)
. (1)
Тогда ![]() и имеет место формула
обращения
и имеет место формула
обращения
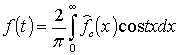 (2)
(2)
для любого ![]() .
.
В той же
работе доказано, что из этой теоремы в качестве следствия можно получить
следующие утверждения для одномерных косинус-рядов.
Следствие А.
Пусть коэффициенты ряда
![]() , (3)
, (3)
где ![]() , удовлетворяют при некотором
, удовлетворяют при некотором ![]() условию
условию
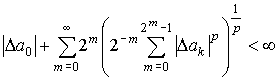 ,
,
![]() ,
, ![]() . Тогда сумма
. Тогда сумма ![]() ряда (3) принадлежит
ряда (3) принадлежит ![]() и ряд (3) является
рядом Фурье функции
и ряд (3) является
рядом Фурье функции ![]() . Следствие А ранее было доказано Г.А.Фоминым другим методом.
. Следствие А ранее было доказано Г.А.Фоминым другим методом.
Кратный
аналог теоремы Фомина для рядов по тригонометрической системе доказан
А.Кузнецовой, для рядов Уолша - Морицем и Шиппом (1991 г.). Такие же вопросы
для рядов по мультипликативной системе Прайса рассматривались Н.Сыздыковой.
Нашей целью
является доказательство двумерного аналога теоремы А. Справедлива
Теорема 1.
Пусть ![]() локально абсолютно
непрерывна по каждой переменной и ее производные
локально абсолютно
непрерывна по каждой переменной и ее производные ![]() и
и ![]() также локально
абсолютно непрерывны по каждой переменной,
также локально
абсолютно непрерывны по каждой переменной, ![]() ,
, ![]() ,
, ![]() и для некоторого
и для некоторого ![]() сходится интеграл
сходится интеграл
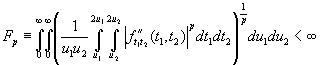 .
.
Тогда ![]() и имеет место формула
обращения
и имеет место формула
обращения
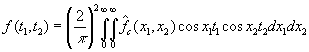
для каждого ![]() .
.
Лемма А. ([1],
стр. 338). Пусть ![]() локально
локально ![]() -интегрируемая функция на
-интегрируемая функция на ![]() при некотором
при некотором ![]() . Тогда для любого
. Тогда для любого ![]() имеет место
неравенство:
имеет место
неравенство:
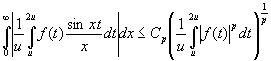 . (4)
. (4)
Теперь
рассмотрим двумерный аналог леммы A.
Лемма 1. Пусть
![]() локально
локально ![]() -интегрируемая функция. Тогда для любых
-интегрируемая функция. Тогда для любых ![]() и
и ![]() имеет место
неравенство
имеет место
неравенство
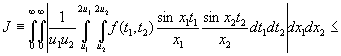
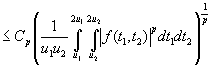 .
.
Доказательство.
На основании леммы А имеет место оценка
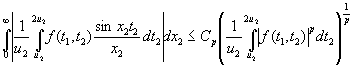
при любом ![]() и фиксированном
и фиксированном ![]() . Следовательно, применяя лемму А еще раз, получим
. Следовательно, применяя лемму А еще раз, получим
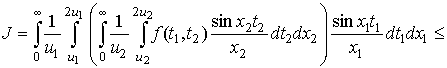
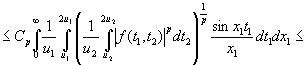
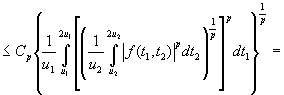
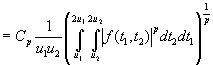 .
.
Отсюда следует требуемая
оценка. Лемма доказана. ■
Лемма 2. Пусть
![]() . Тогда для любого
. Тогда для любого ![]() имеет место равенство
имеет место равенство
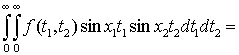
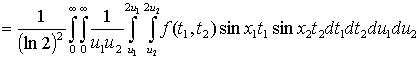 .
.
Доказательство.
На основании теоремы Фубини, меняя пределы интегрирования, получим
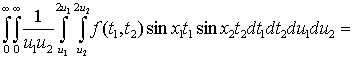
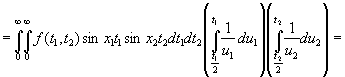
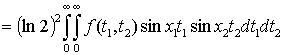 .
.
Отсюда следует условие леммы
2.
Доказательство теоремы 1. Докажем, что ![]() . Для этого проинтегрируем внутренний интеграл.
. Для этого проинтегрируем внутренний интеграл.
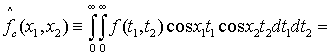
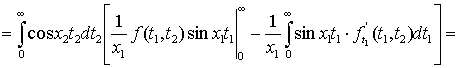
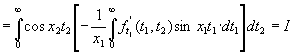 .
.
Далее, интегрируя по частям
интеграл ![]() , получим
, получим
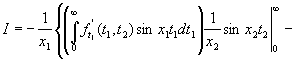
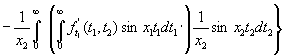 .
.
Учитывая,
что первое слагаемое в ![]() обращается в нуль,
имеем
обращается в нуль,
имеем
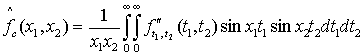
Далее, проинтегрировав это
равенство, на основании лемм 1 и 2 получим
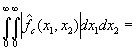
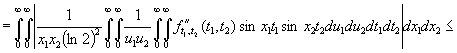
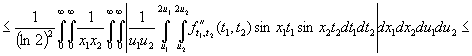
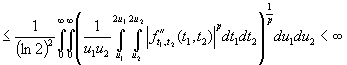 .
.
Следовательно, ![]() . Теорема 1 доказана.
. Теорема 1 доказана.
В следующей
теореме ответим на вопрос ![]() -интегрируемости с весом косинус-преобразования монотонно
убывающей функции.
-интегрируемости с весом косинус-преобразования монотонно
убывающей функции.
Теорема 2.
Пусть ![]() - четная, монотонно
убывающая функция,
- четная, монотонно
убывающая функция, ![]() . Тогда, если
. Тогда, если
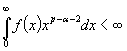 .
.
то
![]() .
.
Для
доказательства данной теоремы нам понадобится следующая
Лемма Б. (Неравенство
Харди [2]). Пусть ![]() и
и ![]() -неотрицательная функция, определенная на
-неотрицательная функция, определенная на ![]() . Тогда
. Тогда
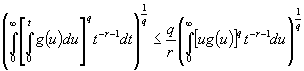 .
.
Доказательство теоремы 2. Так как ![]() не возрастает и
не возрастает и ![]() , то интеграл
, то интеграл
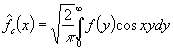
сходится для любого ![]() . Разобьем данный интеграл на две части следующим образом
. Разобьем данный интеграл на две части следующим образом
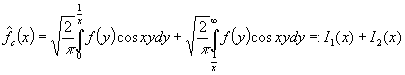 .
.
По второй теореме о среднем
значении
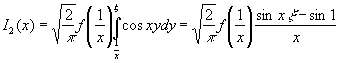 .
.
Поэтому
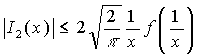
и
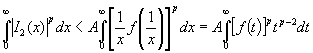 .
.
Далее, так как ![]() не возрастает и
не возрастает и ![]() , то интеграл
, то интеграл
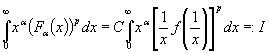 .
.
Выполним замену в интеграле ![]() . Тогда последний интеграл запишется в виде
. Тогда последний интеграл запишется в виде
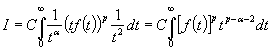 .
.
Теперь проверим, что
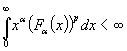 .
.
Для доказательства последнего
неравенства выполним замену в интеграле ![]() и применим к
преобразованному интегралу лемму Б.
и применим к
преобразованному интегралу лемму Б.
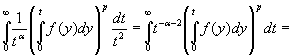
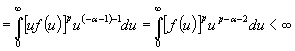 .
.
Теорема доказана.
Литература:
1.
Dang Vu Gians, Moricz F. Lebesgue
integrability of Fourier transforms //Acta Sci. Math. – 1995. – V.60, N1-2. –
P.329-343.
2.
Харди
Г.Г., Литлвуд Дж.И., Полиа Г. Неравенства.-М.:Изд-во ЛКИ, 2008.-456с.