К.ф.-м.н. Бозиев О.Л.

Кабардино-Балкарский государственный университет (г.Нальчик, Россия)

Об одном способе приближенного решения смешанной задачи для нелинейного параболического уравнения

Рассмотрим уравнение Колмогорова–Петровского–Пискунова, возникающее в задачах тепло– и массопереноса, теории горения, биологии, экологии:

(1)

Пусть требуется найти его решение, удовлетворяющее условиям

(2)

(3)

Способ приближенного решения задачи (1) – (3), состоит в последовательной аппроксимации уравнения (1) некоторым рекуррентным соотношением. Для этого начальное значение u⁽⁰⁾(x, t), способ нахождения которого будет описан ниже, используется для начала следующего итерационного процесса.

1. Положить k = 1, где – итерационный индекс.

2. Подставить u^(k–1)(x, t) в уравнение (1), записанное в виде

(4)

3. Решить уравнение (4) при условиях (2) и (3), принимающих вид

Решение данной задачи может быть найдено, в частности, преобразованием к неоднородному уравнению теплопроводности и нахождению его решения с помощью функции Грина (см., например, [1]).

4. Подставить найденную функцию u^(k)(x, t) в итерационное уравнение (4) и найти очередное “уточненное” значение u^(k+1)(x, t).

5. Завершить процесс при выполнении условия

,

где ε – достаточно малое наперед заданное число.

Для нахождения “стартового” значения u⁽⁰⁾(x, t) применим метод редукции к нагруженным уравнениям. Применительно к поставленной задаче он состоит в замене уравнения (1) аппроксимирующим нагруженным уравнением

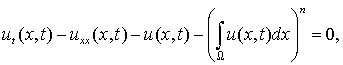(5)

в котором Ω = [0, l].

Следуя [2] будем называть функцию u(x, t) приближенным решением задачи (1) – (3), если она является точным или приближенным решением аппроксимирующей задачи (5), (2), (3).

Введем обозначение тогда будет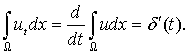

Запишем уравнение (5) в виде

где функция δ(t) пока не определена, после чего проинтегрируем его по x:

Заменим неопределенные интегралы в правой части на определенные в границах от 0 до l, после чего последнее уравнение примет вид

После повторного интегрирования получаем

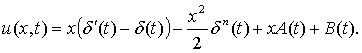(6)

Для определения произвольных функций A(t) и B(t) воспользуемся граничными условиями (3), из которых следует, что

Теперь проинтегрируем последнее уравнение в области Ω. В результате получим относительно функции δ(t) алгебраическое уравнение

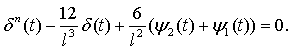(7)

Решение последнего уравнения, подставленное в (5), позволяет получить линейное неоднородное уравнение вида

(8)

в котором f(t) = δⁿ(t) – известная функция. Решение этого уравнения при условиях (2), (3), найденное с помощью функции Грина для уравнения теплопроводности, и будет “стартовым” значением u⁽⁰⁾(x, t), необходимым для начала описанного выше итерационного процесса.

Аналогичный прием был предложен в [3] для нахождения приближенного решения смешанной задачи для квазилинейного гиперболического уравнения, моделирующего некоторые неустановившиеся гидродинамические процессы. Один из сомножителей в нелинейном члене этого уравнения, так же как и в приведенном случае, заменяется интегралом от решения по пространственной переменной, в результате чего уравнение становится нагруженным. В этом случае функция δ(t) определяется решением нелинейного обыкновенного дифференциального уравнения второго порядка. Описанный способ может быть эффективным для решения начально-краевых задач для некоторых классов нелинейных уравнений в частных производных, в частности уравнений, обладающих степенной нелинейностью.

Литература

1. Полянин А.Д. Справочник по линейным уравнениям математической физики: точные решения. – М.: ФИЗМАТЛИТ, 2001. – 576 с.

2. Нахушев А. М. Уравнения математической биологии. – М.: Высшая школа, 1995, 301 с.

3. Бозиев О.Л. Краевые задачи для некоторых классов нагруженных уравнений гиперболического типа. Дисс.…канд. физ.-мат. наук. – Нальчик, 2000. – 94 с.