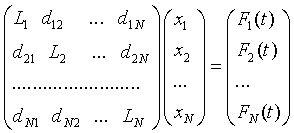Ìàòåìàòèêà/1.Äèôôåðåíöèàëüíûå
è èíòåãðàëüíûå óðàâíåíèÿ
Dokukova N.À., Kaftaikina E.N., Golod S.V., Orehov M.B., Konon P.N.
Belarusian State University, Belarus
EXPERIMENTAL
ANALYSIS OF METHODS OF CALCULATING THE DYNAMIC OF THREE-ELEMENT MECHANICAL
SYSTEM
Calculation
of multielement mechanical
system was introduced in [1].
The general results obtained allow to
determine the criteria for
the selection of rational physical and
geometrical parameters for the original mechanical system based on sustainability and quality of the dynamic model [2, 3]. In this paper a practical
confirmation of the analytical calculation of
the vibrational motions of the
example three-element mechanical
system is presented. Experimental analysis of methods of calculating natural vibrations
of a dynamical system was carried out
using a special measuring equipment:
strain gauge transducer to measure the vibration
acceleration, multi-channel mobile measuring amplifier, laptop, software Catman
Professional, universal interface
software package with a set of mathematical functions (Fig. 1).
The experiment description. The purpose of
experiment is determination of the kinematic
characteristics of the experimental model (Fig. 1).
Experiment procedure: 1. Identify
the attenuation characteristics by acceleration of the total
mass suspended on a spring
c1 and simply
supported on hydrodynamic damping with water for
the subsequent calculation of the
damping coefficient of vibrations; 2. Determine the acceleration
of the natural oscillations of the
masses m1, m2, m3; 3. Determine
the frequency characteristics (frequency spectra) of the
masses m1, m2, m3 by acceleration;
4. Compare the obtained experimental
results of the prototype with the analytical results obtained by the method of calculating the dynamics of multicomponent mechanical systems [1].
Measuring equipment: strain gauge transducer produced by NATI,
mobile measuring amplifier «Spider-8», software Catman Professional.
Figure 1 -
experimental model
of mechanical system and measuring equipment
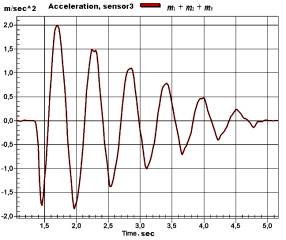
Experiment to
accelerate total mass (m1+m2+m3), suspended on a spring c1 and simply supported on
hydrodynamic damping with water was conducted for the calculation of the damping
coefficient of vibrations for external hydrodynamic
attenuation (fig.
2), numerical value was obtained b3=2 9.31 ln(8.0)/(5-1.58) = 11.3214 N*sec/m, where m1=4.41 kg, m2=3.37
kg, m3=1.53
kg.
a
b
Figure 2 -
a-hydrodynamic damping with water; b- attenuation vibrations of total mass acceleration (m1+m2+m3)
|
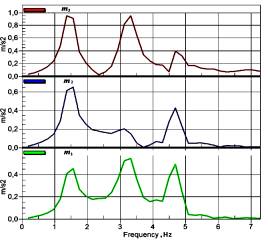
Figure 3 - Frequency
spectra of vibrations for acceleration (experimental results) |
Kinematic excitation of vibrations occurred
as follows: lower mass m1 is pulled down to a
distance of 3.3 cm, in line with this the rest masses have taken their position in space and deviated by 3.3 cm m2, m1
of 2.5 cm, respectively, relative to its equilibrium position.
Then check the
hardware included and the lower
load is released. The experimental results are
presented in the graphs (Fig.
4). |
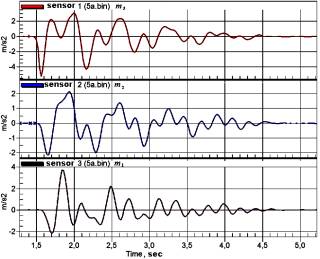
a b
Figure 4 -
Experimental results (a- accelerations, b-displacements)
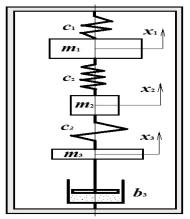
Analytical calculation. Vibrations of mechanical systems with many
degrees of freedom equal to 
(Fig. 5) can be represented as a system of
three linear differential equations of
second order:
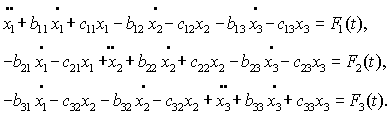(1)
Introduce the notation similar to those shown in [2,3]:
|
|
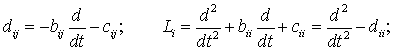
Than system (1) using notation can be
reproducible in the matrix form:
|
System
(1) with certain non-singular
linear transformations can be
reduced to a system of independent linear ordinary differential equations of
sixth order disconnected with
each other:
.
The
right side consists of a
combination of functions 
and their derivatives [1]. The dynamic scheme (Fig. 4) shows the model with three degrees of freedom and the physical parameters: elasticity coefficients c1=1160.8 N/m, c2=960.7 N/m, c3=695.5 N/m, damping b3 = 11.3214 N*sec/ m, external forces F1=0 N, F2=0 N, F3=0 by. The initial conditions are taken from experiment x1(t) = -0.025, x2(t) = -0.033, x3(t) = -0.033, x1¢(t) = 0.0, x2¢(t) =0.0, x3¢(t) = 0.0. The system of equations (1) in matrix form becomes:
. (3)
Matrix of elastic and damping coefficients of the canonical representations [1-3] chose
the following:
, 
, 
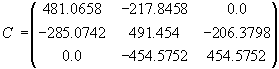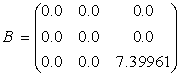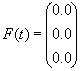
Derived by the general system of three independent differential
equations of sixth order, represented by the relations, for which
the characteristic equation takes the form: h6+1427.095h4+522587.67h2+7.399h5+7196.26 h3+1289896.2 h+34110054 =0,
find a solution to a system of three non-connected
between a differential
equation of natural vibrations of a dynamical system with three degrees of
freedom (Fig. 1) in an analytical form:
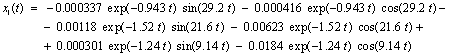
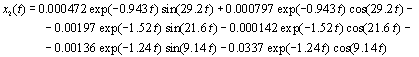
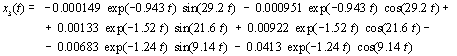
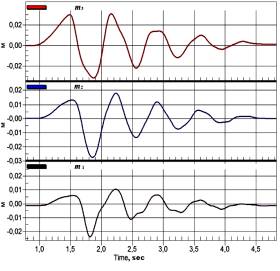
Graphs of
analytical solutions of the homogeneous differential equations describing the oscillations of a system with three degrees of freedom, and
experimental (Fig. 4) are presented in comparison to Figure 6-7 for the
time interval from 0sec to 4sec way to overlay. It can be seen in an acceptable agreement of the results, the
correlation factors which affected the imbalance of
structural elements in the vertical direction due
to minor distortions of the vibrational motions in
three dimensions after kinematic excitation of the system. This circumstance was
not considered in the analytical calculation to
facilitate comparison of a small number of parameters. The
aim of the study was supplied only vertical
components. Therefore, emerging backlash and
distortions of the model that were neglected in
the calculation, influenced by the slight discrepancy
between the parameters. On
this basis, it
can be argued that the method of calculation [1-5], multiple-dynamical systems with a consistent application of differential operators is correct. It allows to manage dynamic processes of oscillations and vibrations of complex mechanical systems,
adjust the field of high frequency damping necessary
to theoretically analyze the stability conditions of the mechanical system to obtain accurate
results of the calculations - displacement, velocity, acceleration, frequency response, to identify areas of the resonances, the spectrum acceleration was found, the transmission
coefficients of mechanisms links load.
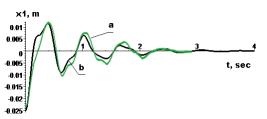
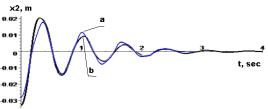
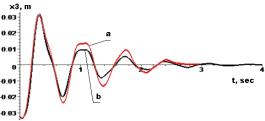
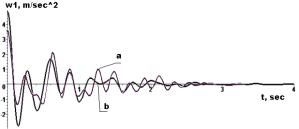
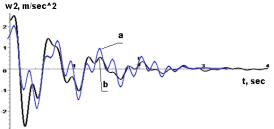
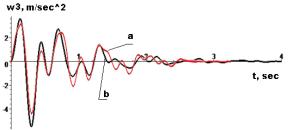
Figure 6 - à-
experimental curves; b-accurate analytical solutions of displacements 
and accelerations 
of the homogeneous differential
equations system
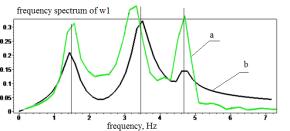
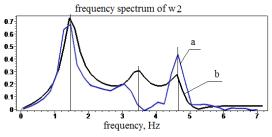
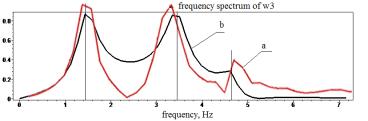
Figure 7 - frequency spectrum of accelerations 
of the homogeneous
differential equations system at the interval [0,7] Hz (à-experimental curves; b-accurate analytical)
The
system of three coupled homogeneous second order differential
equations with separable variables is integrated analytically. Accurate analytical results of
decaying oscillations were obtained using known initial velocity and displacement data provided
by the method. The
analytical results are compared with experimental data. Measurement
error the most impact on low-level components - moving mass
m2 and its frequency response. Theoretical and
experimental data fairly well correlated. The average deviation of them
is the 0,82. The
diagrams of the frequency spectra can
be observed coincidence of natural frequencies.
References
1. Dokukova,
N.A. General patterns of improper vibrations of dynamical
systems with arbitrary number of degrees of freedom / N.A. Dokukova,
E.N. Kaftaikina, V.V. Zenkovich // News on
the scientific progression -2011: The material for the 7-and
international scientific
and practical conference, Sofia, 17-25 August 2011.: 9 tons / Editorial Board.: M. Petkov. -
Sofia: GRAD-BG
Ltd., 2011.-. T. 9. -
S. 56 -64.
2. Dokukova N.A., Vysotsky M.S., Konon P.N. The method
of investigation of
mechanical vibrating
systems by means of
differential operators / /Reports
of the National Academy of
Sciences of Belarus. 2006. - T. 50. Number 1. S.114-119.
3. Dokukova
N.A., Konon P.N. General laws governing in mechanical vibratory systems //
Journal of Engineering Physics and Thermophysics, 2006, Volume 79, Number 4, Pages 824-831, Publisher Springer New York, ISSN:
1062-0125.
4. Dokukova
N.A., Konon P.N. Generalities of passive vibration dampers isolating
vibrations // Journal of Engineering Physics and Thermophysics, 2006,
Volume 79, Number 2, Pages
412-417, Publisher Springer New York, ISSN: 1062-0125.
5. Dokukova
N.A., Konon P.N., Kaftaikina E.N. Nonnatural vibrations of hydraulic
shock-absorbers // Journal of Engineering Physics and Thermophysics, 2008,
Volume 81, Number 6, Pages
1191-1196, Publisher Springer New York, ISSN: 1062-0125.