Математика/5 Математическое планирование
старший
преподаватель Акмолдина А.И.
ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ПРОНИЦАЕМОСТИ
ПЛАСТА МЕТОД ИТЕРАЦИЙ
Костанайский государственный университет им. А.
Байтурсынова
1. Постановка задачи
Рассмотрим случай пласта, проницаемость вблизи
скважины (при забойной зоне) отличается от проницаемости во внешней области.
Такой случай представляет большой практический интерес. Процесс бурения и
оборудования нефтяной или газовой скважины и ее последующая работа изменяют
проницаемость в при забойной зоне, чаще всего уменьшают ее. Для восстановления
и увеличения проницаемости при забойной зоны производятся различные обработки
ее: промывка кислотой, образование трещин путем закачки жидкости под высоким
давлением (гидравлический разрыв пласта) или взрывом (торпедирование) и др.
Исследование скважин методом восстановления давления позволяет выяснить
необходимость проведения таких выработок, т.е. определить снижение
проницаемости в при забойной зоне по сравнению
с проницаемостью остальной части пласта, а впоследствии – оценить
эффективность проведенных работ.
В области ![]() решается задача
решается задача
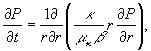 (1.1)
(1.1)
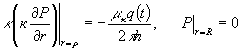 (1.2)
(1.2)
![]() (1.3)
(1.3)
На границе ![]() выполняются условия
непрерывности давлений и потоков:
выполняются условия
непрерывности давлений и потоков:
![]()
Если ввести обозначение ![]() , скачок функций при
, скачок функций при ![]() , то внутренние граничные условия записываются в виде
, то внутренние граничные условия записываются в виде
![]() (1.4)
(1.4)
Здесь ![]() - граница при забойной зоны с внешней области,
- граница при забойной зоны с внешней области, ![]() - вязкость нефти,
- вязкость нефти, ![]() ;
; ![]() - проницаемость пласта,
- проницаемость пласта, ![]() ;
; ![]() - упругоемкость пласта,
- упругоемкость пласта, ![]() .
.
Кроме этого, на скважине, т.е. при ![]() задается давление
пласта
задается давление
пласта
![]() (1.5)
(1.5)
Требуется определить ![]() и
и ![]() .
.
1.2. Задача с обратным временем
Задается начальное приближение ![]() . Соответствующее решения системы (1.1)-(1.4) обозначим через
. Соответствующее решения системы (1.1)-(1.4) обозначим через
![]() . Следующее приближение коэффициента проницаемости пласта
обозначим через
. Следующее приближение коэффициента проницаемости пласта
обозначим через ![]() , а соответствующее решение системы (1.1)-(1.4) через
, а соответствующее решение системы (1.1)-(1.4) через ![]() . Будем искать функцию
. Будем искать функцию ![]() . Для этого система 1.1)-(1.4) записывается относительно
функций
. Для этого система 1.1)-(1.4) записывается относительно
функций ![]() :
:
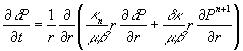 (1.6)
(1.6)
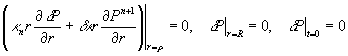 (1.7)
(1.7)
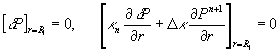 (1.8)
(1.8)
Умножим (1.6) на произвольную функцию ![]() и интегрируем по
области
и интегрируем по
области ![]() . Тогда
. Тогда
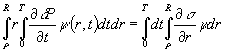
Здесь ![]()
Применяем формулу интегрирования по частям по
переменной ![]() и
и ![]() :
:
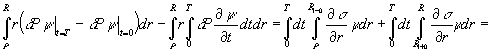
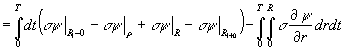
В силу начально-граничных условий (1.7) заключаем, что
![]()
Дополнительно потребуем, чтобы
![]()
Тогда,
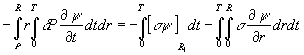
Рассмотрим скачок функций ![]() . Потребуем, что функция
. Потребуем, что функция ![]() в точке
в точке ![]() непрерывна.
непрерывна.
Тогда на основе (1.8) выводится равенство
![]()
С учетом полученного равенства, последнее интегральное
соотношение записывается в виде:
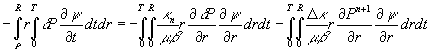
Первый интеграл в правой части знака равенство снова
интегрируем по частям по переменной ![]() . Тогда
. Тогда
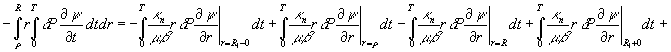
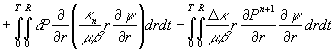
Учитывая граничное условие ![]() и группируя подобные слагаемые получим
и группируя подобные слагаемые получим
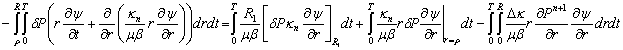 Предположим, что
Предположим, что
![]() и
и ![]()
Учитывая непрерывность функций ![]() в точке
в точке ![]() , преобразуем
, преобразуем
![]()
С учетом полученных равенств интегральное соотношение
записывается в виде
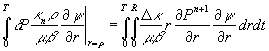
Пусть имеет место равенство
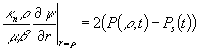 , тогда получится равенство
, тогда получится равенство
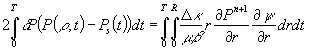 (1.9)
(1.9)
Полученная сопряженная задача записывается в виде
![]() (1.10)
(1.10)
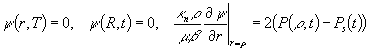 (1.11)
(1.11)
![]() (1.12)
(1.12)
Литература:
1. Г.И. Баренблатт, В.М. Ентов, В.М. Рыжик. Теория
нестационарной фильтрации жидкости и газа. – Издательство Нейра, 1992