В.Є. Білозьоров, С.А. Волкова, Л.В. Підгорна

ДВНЗ «УДХТУ», каф. ОТ та ПМ

м. Дніпропетрівськ, пр. Гагаріна, 8

ДОСЛІДЖЕННІ СТІЙКОСТІ РОЗВ’ЯЗКІВ РІВНЯНЬ ЛОТКИ-ВОЛЬТЕРРИ

Список літератури

Чернышенко С.В. Нелинейные методы анализа динамики лесных биогеоценозов. – Днепропетровск: Издательство Днепропетровского национального университета, 2005. – 512 с.

Takeuchi Y. Global Dynamical Properties of Lotka-Volterra Systems. – World Scientific Publishing Co., Singapure, New Jersey, London, Hong Kong, 1996. – 302 p.

Lotka A.G. Elements of physical biology. – Baltimore: Williams and Wilkens, 1925. – 254 p.

Volterra V. Fluctuations in the abundance of a species considered mathematically – Nature. 1926. – Vol. 188. – P. 558-560.

Арнольд В.И. Дополнительные главы теории обыкновенных дифференциальных уравнений. – М.: Наука, 1978. – 304 с.

Khalil H.K. Nonlinear Systems (Second Edition) – New-York: Prentice Hall, Upper Saddle River, 1995. – 730 p.

Вступ

Добре відомо [1,2], яку важливу роль грають рівняння Лотки-Вольтерри в задачах математичної біології. Ці рівняння описують різні динамічні аспекти взаємодії популяцій біологічних видів та у багатьох випадках є основними моделями для прогнозування їхнього розвитку.

В цій роботі вивчається новий підхід до дослідження стійкості розв’язків рівнянь Лотки-Вольтерри, що базується на переході до логарифмічних змінних. За допомогою цього підходу отримані нові результати, які стосуються глобальної стійкості невід’ємних положень рівноваги.

Постановка задачі

Позначимо через дійсний лінійний простір вектор-стовпців вимірності n (надалі ми будемо називати його простором станів), а через – невідомий вектор з (що називається надалі вектором станів), координати якого є функціями часу t. Розглянемо систему звичайних квадратичних диференційних рівнянь, що описують динамічну модель розвитку системи біологічних популяцій, яка відома як модель Лотки-Вольтерри [3,4]:

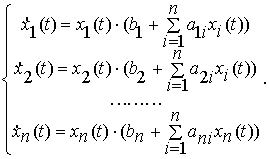(1)

Надалі будемо вважати, що для системи (1)

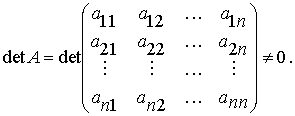
Очевидно, що система (1) має особливих точок (положень рівноваги), які знаходяться як розв’язки системи рівнянь

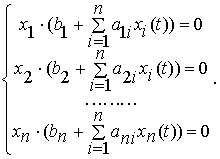
Позначимо ці точки як

Перейдемо в системі (1) до нових змінних . Тоді для кожного одержимо квадратичну систему такого вигляду:

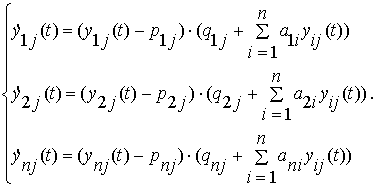(2)

Дослідження кожної із систем (2) можна проводити в околі початку координат.

Висновки

Отримані достатні умови того, щоб для системи (1) перший ортант був областю глобальної стійкості. Це дозволяє вказати характеристики навколишнього середовища, при яких можливо стабільне спільне існування n біологічних популяцій при будь-яких початкових умовах.