Mathematics /4. Applied mathematics

Nsangou M. M.

People’s Friendship University of Russia, Moscow, Russia

ANALYSIS OF THE QUEUE MODEL WITH THE BUSY PERIOD, ORDINARY AND WORKING VACATIONS

In this paper, we consider a simplified vacation model, investigating a system with a fixed size of the costumers queue. When the server becomes empty, it either goes on an ordinary vacation or takes a working vacation. In the working vacation, a costumer is served at a lower rate, and at the instants of the service completion, the vacation is interrupted and the server resumes to a regular busy period or continues the vacation according to Bernoulli schedule.

Keywords: server vacations, working vacations, Bernoulli vacation schedule.

Introduction

The vacation queue models have been investigated extensively in view of their application in computer systems, production managing, communication networks particularly the IP access networks [3]. In a classical vacation queue, the server completely stops serving customers and may do some additional works or maintain servers during a vacation [2]; while on a working vacation, the server continues to work at a lower rate. The goal of the paper is to model some server ability characteristics during a busy cycle, fixing the size of the costumers queue as for some really systems. The recurrent formulas of the stationary probabilities are obtained, the state or blocking probabilities and queue length managing parameters are evaluated.

1. Model description

In this section, we make the following assumptions to describe the model with both ordinary and working vacations. Costumers reach the system according to a Poisson process with compound intensity and there is one server in the system. Service times are assumed to be exponentially distributed with mean; the rate is. As soon as the server finishes a service, it can begin a vacation of random variable, and takes an ordinary vacation or a working vacation with probability, where. The ordinary and working vacations lengths are exponentially distributed with parameters and respectively. During an ordinary vacation the server will stops serving even if there are new arrivals in the system. In the working vacation, costumers are served at a lower rate; furthermore, at the instants of service completion, the vacation is interrupted and the server resumes to a regular busy period with probability (if there are costumers in the queue) or continues the vacation with probability. The decisions of choosing vacations as well as interruptions are mutually independent and all aforementioned variables are independent of each other; the service order is First Come First Served.

2. Model analysis

Let be the number of costumers in the system at time and let define, , the states of the server, respectively for working, ordinary vacations and busy period at time t. Let consider, that all the steady state probabilities existence conditions are realized, then can be analyzed as a QBD (Queuing Birth and Dearth) process with states space.

Under the steady state conditions, and according to the exponentially distributed service delay, is a standard continuous-time Markov chain. The followed system can be illustrated by the states transition diagram in figure 1, with a queue size is fixed and equal to.

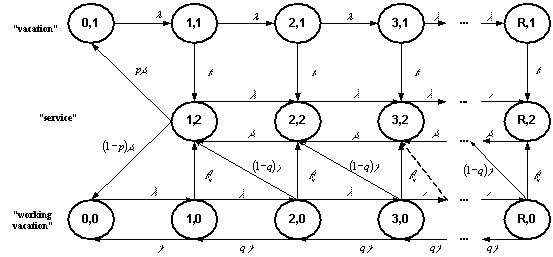
Fig. 1. State transition diagram of the QBD process

Let, be the steady state probability and; from the Markov chains theory, it follows that has a unique equilibrium distribution which satisfies the following family of equations.

;

;

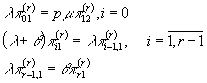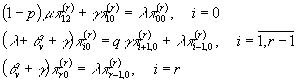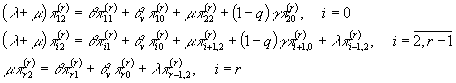
And the partial balance equations system,

;

.

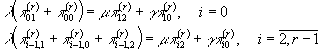To find the state probabilities, let define and , we will check , as so that, and , . Making required transformations, and solving the systems of above equations, we can enounce the next algorithm for, which calculate the distribution, .

Step 1. Finding of the solution of the recurrent equation:

.

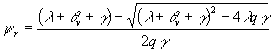Step 2. Calculating of the probabilities constants:

, , and , where,

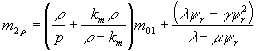; and .

Step 3. Calculating of the parameter:

, where, intermediate constants ,

, .

Step 4. Calculating of all steady state probabilities, as follows

, where,

; and

.

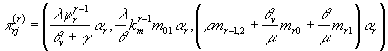3. Distribution of the server ability characteristics

The most important QoS parameters are the different types of probabilities, the queue length and average sojourn time of a costumer in the system. Let define states probabilities as follows: ; ; , the probabilities that the server is in “regular vacation”, “busy period” and “working vacation” respectively and can be expressed as:

Another important length characteristic is the blocking probability defined as:

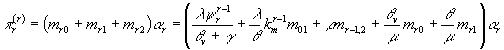
For the average queue length analysis and the sojourn time of a costumer in the system, we use the probability generating function (pgf) of the queue and, after some transformations, we obtained,

;

,

.

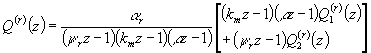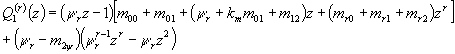The average queue length can be founded as:

;

,

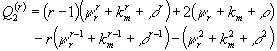
Concluding this part, let remark that,

.

и is the average queue length for the ordinary М/М/1/R model.

The sojourn time is founded using the Littla formula as follows:

.

Furthermore, the highest load time can be measured trough the variation and derivate parameters like:

;

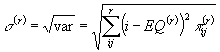- Queue length variation.

4. Numerical analysis

In this section, we take the initial values from [2] and [5] under the assumptions that. So let take, , , , , maximum of and .

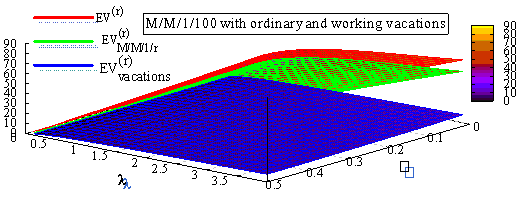
Fig. 2. The average sojourn time in function of intensities and

The fig. 2 demonstrates that the model we built, satisfies the vacation type one as the costumer sojourn time property stochastically was proofed. As we can observe, the growth of the customers or the vacation service loads improve the sojourn time.

Conclusion

The work in this paper can be used to model many practical problems. For example, the wireless mobile devices accessing the wireless networks with different data rates can also be analyzed. Numerically, the decomposition property of the queue length and sojourn time distributions was proofed and the algorithm of steady state probabilities calculation was founded; using these results, we defined the states and blocking probabilities, the queue length and his variation during a time period.

References

1. Hongbo Zhang and Dinghua Shi, The M/M/1 Queue with Bernoulli-Schedule-Controlled Vacation and Vacation Interruption. International Journal of Information and Management Sciences 20 (2009), 579-587.

2. Naishuo Tian , Xinqiu Zhao and Kaiyu Wang, The M/M/1 Queue with Single Working Vacation. International Journal of Information and Management Sciences Volume 19, Number 4, pp. 621-634, 2008.

3. Servi, L. and Finn, S., M/M/1 queues with working vacations (M/M/1/WV), Perform. Eval., Vol.50, pp.41-52, 2002.

4. Neuts, M., Matrix-Geometric Solutions in Stochastic models, Johns Hopkins University Press, Baltimore, 1983.

5. C. Chi, R.Hao, D.Wang, Z.Cao “IMS Presence Server: Traffic Analysis & Performance Modelling.