К.т.н. Твердоступ Н.И.

Днепропетровский национальный университет им. Олеся Гончара

О КОМПЕНСАЦИИ РЕАКТАНСА ИНДУКТИВНОГО ДАТЧИКА

 

Применение  индуктивных датчиков в низкочастотных резонансных устройствах измерения и контроля в ряде случаев ограничивается малыми значениями их собственных индуктивности, добротности и невысокой чувствительностью к контролируемому параметру. Поэтому актуальным является создание устройств, позволяющих увеличивать индуктивность датчика до необходимого значения с одновременным повышением чувствительности контроля.

 Анализ результатов, полученных в  [1], обосновывает целесообразность использования  комбинированной операционной схемы для создания умножителей индуктивности. Линейная комбинированная операционная схема (ЛКОС)  обладает свойством масштабирования импеданса с сохранением знака, что позволяет  на ее основе создавать умножители реактансов [2].

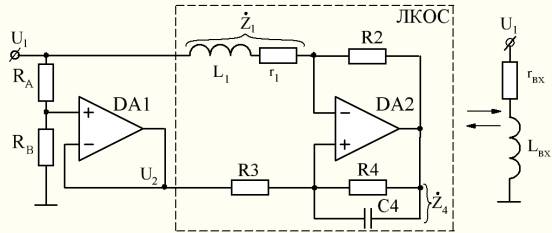
         В линейной комбинированной операционной схеме  (рис.1) с индуктивным импедансом в цепи отрицательной обратной связи характерным является наличие комбинированной обратной связи, а также то, что внешние сигналы возбуждения поступают синфазно на оба входа операционного усилителя. Из

                                               а)                                               б)

Рис. 1 – Линейная комбинированная операционная схема (а) и ее

              эквивалент (б)

выводов к работе [1] следует, что входной импеданс такой схемы равен

 = (                                    (1)                                             

где – комплексный импеданс индуктивности L1 с активным сопротивлением r1;  R2 , R3  – активные сопротивления цепи комбинированной обратной связи усилителя DA2;  – комплексный импеданс параллельно соединенного сопротивления   и емкости  ; n = U2 / U1, U1 и U2 – напряжения сигналов возбуждения. Повторитель на усилителе DA1 с резистивным делителем RА, RВ представляет собой источник напряжения возбуждения U2, синфазного входному напряжению U1.

Из (1) следует, что отношение n напряжений возбуждения оказывает основное  влияние на величину , а именно: при n →1 и U2 < U1 значение входного импеданса существенно увеличивается. Отношение n напряжений возбуждения можно представить через отношение сопротивлений делителя в виде

                                              (2)

тогда входной импеданс , выраженный через параметры схемы, будет                              

                   (3)

Справедливо также, что , представленный через входные параметры, равен

 = rвх + jωLвх,                                                      (4)

где rвх, Lвх – входные активное  сопротивление и индуктивность. Тогда из (3) и (4) следуют выражения активной и индуктивной составляющих входного импеданса

                                 (5)

                                  (6)                                

показывающие, что в настоящей схеме индуктивность L1 с активным сопротивлением  r1 преобразуются во входные индуктивность   Lвх и сопротивление rвх с коэффициентом умножения равным

                                                (7)                                                     

 который, при выполнении условия  RB >> RA, может принимать большие значения. Из (5) следует, что умножение активного сопротивления r1 сопровождается его компенсацией  отрицательной активной составляющей входного импеданса ЛКОС равной

                                             (8)

При  → r1 входное сопротивление rвх → 0, что указывает  на возможность повышения добротности индуктивности. Более детально о повышении добротности умноженной индуктивности рассмотрено в [2].

         Из (6) следует, что умножение индуктивности L1 на коэффициент m происходит одновременно с уменьшением ее начального значения на величину , имеющей размерность индуктивности. Эту величину будем называть компенсирующей индуктивностью Lк. Выражение (6) представим в виде

 .                                               (9)

Допустим, что под воздействием контролируемого параметра индуктивность L1 изменится на величину ΔL1, тогда входная индуктивность станет

 .                            (10)

Из (9), (10) следует, что абсолютное приращение входной индуктивности составит

                                                   (11)

а относительное приращение

                                        (12)

причем, при Видно, что абсолютное приращение входной индуктивности определяется коэффициентом умножения m , а относительное приращение – величиной компенсирующей индуктивности Lк. Это показывает, что в рассматриваемой схеме возможно масштабирование индуктивности датчика с управлением величины чувствительности к контролируемому параметру.

Умножитель индуктивности по схеме на рис.1 был построен на операционных усилителях МСР604, в качестве умножаемого импеданса использовалась катушка с индуктивностью L1 = 21,06 мГн и активным сопротивлением r1 = 5,4  Ом, исследования проводились на частоте 1 кГц при R4 = ∞. 

Результаты исследования возможности умножения индуктивного импеданса с компенсацией его начального реактанса показаны на рис. 2 в виде экспериментальных зависимостей (в логарифмическом масштабе) входной индуктивности Lвх (в мГн) как функции компенсирующей индуктивности Lк при различных коэффициентах умножения  m. Видно, что без компенсации начального

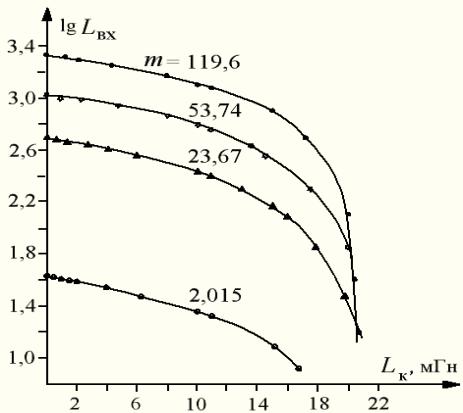
Рис. 2 – Входная индуктивность Lвх как функция компенсирующей Lк

 

 реактанса индуктивности L1 (при Lк = 0) входная индуктивность Lвх в зависимости от коэффициента умножения m изменяется на два порядка и достигает  значения 2,12 Гн при m = 119,6. При увеличении компенсирующей индуктивности Lк входная индуктивность уменьшается от максимальной величины  до значений меньших начального L1. Эксперимент подтверждает возможность  управления величиной входной индуктивности в широких пределах с помощью параметров m и  Lк согласно выражению (9). 

         Увеличение абсолютного приращения входной индуктивности Lвх от коэффициента умножения m согласно (11) подтверждается экспериментальными зависимостями на рис. 3. Здесь при изменении индуктивности датчика L1 на величину ΔL1 = 0,71 мГн абсолютное приращение входной индуктивности ΔLвх возрастает на два порядка при m ≥ 100.

 

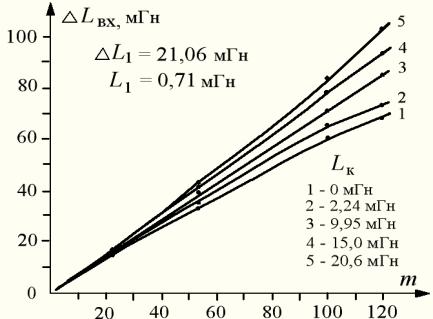
Рис. 3 – Зависимости приращения входной индуктивности ΔLвх от

                       коэффициента умножения m для разных значений Lк

             

         На рис. 4 показаны зависимости относительного приращения (в процен-

тах) ΔLвх/ Lвх входной индуктивности от компенсирующей  Lк для разных значений коэффициента умножения m. Видно, что значение Lк существенно увеличивает  относительное приращение, так, при Lк = 0  ΔLвх/ Lвх = 3,37%,  а при воз-                        

растании Lк до 20,44 мГн  ΔLвх/ Lвх увеличивается до 270%.

         На экспериментальных зависимостях наблюдаются систематические отклонения от расчетных. Отклонения имеют мультипликативный характер и достигают до 20%. Их наличие объясняется тем, что исходное выражение (1) справедливо для идеальной модели операционного усилителя.

 

 

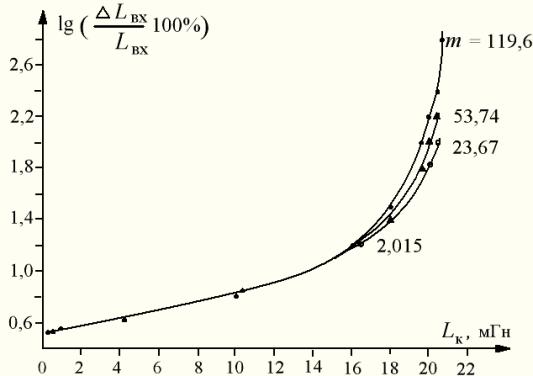
Рис. 4 – Зависимости относительного приращения  ΔLвх/ Lвх

                         входной индуктивности от компенсирующей Lк

        

         Вывод. Исследованиями установлено, что введение в умножитель индуктивности на основе комбинированной операционной схемы цепи компенсации начального реактанса индуктивного датчика позволяет повысить его чувствительность к контролируемому параметру.

 

Литература:

1.   Твердоступ Н.И. Обобщенная модель преобразователей импеданса // Вісник Дніпропетр. ун-ту. Фізика. Радіоелектроніка. – 2010. – Вип. 17, №2. – С. 103 - 108.

2.   Твердоступ Н.И. Высокодобротный умножитель индуктивности // Системні технології. Регіональний міжвузівський збірник наукових праць. – Випуск 1(72). – Дніпропетровськ, 2012. - С. 100 – 105.