К.т.н. Твердоступ Н.И., студент Борисов С.Ю.

Днепропетровский национальный университет им. Олеся Гончара

О ВОЗМОЖНОСТЯХ МЕТОДА ТРЁХ ВОЛЬТМЕТРОВ ДЛЯ ИЗМЕРЕНИЯ СОСТАВЛЯЮЩИХ ИНДУКТИВНОГО

ИМПЕДАНСА

Среди методов измерения индуктивного импеданса [1] выделяется метод трех вольтметров [2], который используют для определения мощности, потребляемой приемником электрической энергии, его активного сопротивления, реактанса и полного сопротивления на промышленных частотах (50, 400 Гц). Достоинством метода является эксплуатационная простота и удобство, заключающееся в том, что для измерения параметров приёмника достаточно всего лишь определить напряжения на трёх участках электрической цепи, состоящей из приёмника электрической энергии с последовательно включенным образцовым активным сопротивлением.

Представляет интерес оценка возможностей метода трёх вольтметров для измерения составляющих индуктивного импеданса а также определения их частотных характеристик в диапазоне выше промышленных частот.

R_o

I

На рис.1 представлена эквивалентная схема измерительной цепи (а) для

Z_x

U_x

E

r

L

U_o

а) б)

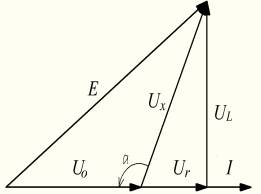
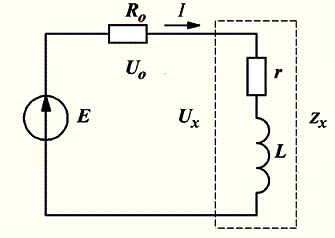
Рис.1 – Измерительная цепь для метода трёх вольтметров (а) и её

векторная диаграмма напряжений и тока (б)

определения составляющих индуктивного импеданса методом трёх вольтметров и её векторная диаграмма (б), где Е – напряжение генератора гармонических колебаний; R_o – образцовое сопротивление; L, r – индуктивность и активное сопротивление измеряемого импеданса ; U_o, U_x – падения напряжения на образцовом сопротивлении и измеряемом импедансе; U_L, U_r – реактивная и активная составляющие напряжения U_x; I – ток в измерительной цепи. Импедансы измеряемой индуктивности и измерительной цепи имеют вид

= , (1)

= , (2)

где ω – частота колебаний гармонического генератора E. Для последовательной цепи значения импедансов можно представить как

=, = . (3)

Из (1) – (3) следует система уравнений

=, (4)

= , (5)

решение которой позволяет получить выражения для активной составляющей индуктивного импеданса

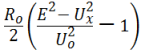= (6)

и его индуктивности

L = 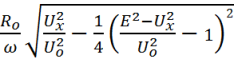. (7)

Из двух последних выражений следует, что величины и L можно найти измерением напряжений , и с последующим вычислением по (6) и (7). Следует отметить, что найденные составляющие индуктивного импеданса и L будут действительными и положительными только при выполнении условия

, (8)

на векторной диаграмме (рис. 1б) это означает, что угол должен принимать

значения .

Для определения возможности измерения составляющих индуктивного импеданса была собрана измерительная схема согласно рис.1а. В качестве измеряемого импеданса использованы образцовые меры индуктивности типа

L-0170 III разряда класса 0,2. Измерения проводились на частоте 1 кГц вольтметром В7-27А/1 с использованием генератора Г3-118. В таблице 1 представлены результаты измерений, где L_o – номинальные значения образцовых мер индуктивности; L_д , r_д - действительные значения индуктивностей и активного сопротивления образцовых мер, полученные мостовым измерителем Е7-8; L, r –индуктивность и активное сопротивление образцовых мер, определённые методом трёх вольтметров.

Таблица 1

Lo, мГн	0,2	0,5	1	2	5	10	20	50	100	200
Lд, мГн	0,201	0,501	1	1,999	4,997	10	20,01	49,99	100	199,9
rд, Ом	1,612	1,944	2,97	4,73	9,98	20,6	75,2	125,5	294	241
L, мГн	0,225	0,518	0,997	1,984	4,907	9,992	19,9	49,98	99,97	200,5
r, Ом	1,499	1,995	2,987	4,948	11,67	20,68	76,92	125,6	292,7	217,6

Используя метод наименьших квадратов получены уравнения линейной регрессии для индуктивности L = f (L_д)

L = – 0,0641 + 1,0026L_д (9)

и активного сопротивления r = (r_д)

r = 1,0182 + 0,9601r_д; (10)

при уровне значимости 0,001 коэффициенты корреляции составили для индуктивности 1, для активного сопротивления 0,9983; среднеквадратическое отклонение отдельного измерения индуктивности = 0,1168 мГн, активного сопротивления = 6,5419 Ом, средняя относительная погрешность измерения индуктивности составила 0,3%, активного сопротивления – 8,65%.

Результаты исследования частотных характеристик показаны на рис. 2.

Экспериментальные частотные зависимости индуктивности L, активного сопротивления r и добротности Q определены в диапазоне 0,1 – 100 кГц. В качестве исследуемого индуктивного импеданса использовалась образцовая мера с индуктивностью L_o = 5 мГн, омическим сопротивлением 8,8 Ом и добротностью 140. Образцовым сопротивлением R_o был выбран резистор типа МЛТ-2 с активным сопротивлением 1475 Ом (на частоте 1 кГц).

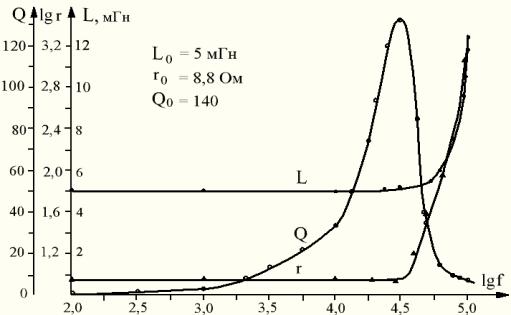
Рис.2 - Частотные характеристики индуктивности L , активного

сопротивления r и добротности Q образцовой меры

индуктивности (L_o = 5 мГн)

Из полученных зависимостей видно, что в диапазоне частот от 0.1 до 30 кГц активное сопротивление r и индуктивность L остаются практически неизменными с отклонениями в пределах погрешности эксперимента. После 30 кГц активное сопротивление r начинает увеличивать свое значение, что можно объяснить возрастающим влиянием эффекта близости и скин-эффекта. Также наблюдается увеличение индуктивности L из-за шунтирующего влияния распределённой ёмкости катушки и измерительной цепи в целом, которые образуют с индуктивностью параллельный контур с некоторой частотой собственного резонанса f_o. С ростом частоты f при ff_o импеданс параллельного контура увеличивается, что приводит к кажущемуся увеличению индуктивности L. Это явление вносит погрешность в определение индуктивности на частотах, приближающихся к частоте собственного резонанса катушки. Погрешность возможно уменьшить при условии учета величины распределенной емкости, для этого потребуется рассмотрение несколько другой эквивалентной схемы измерительной цепи, учитывающей межвитковую емкость измеряемой катушки, входную емкость измерительных приборов и соединительных кабелей.

Частотная зависимость добротности Q = 2fL/r исследуемой образцовой меры индуктивности имеет максимум Q = 133 на частоте f = 30 кГц, величина которого практически совпадает с добротностью, указанной в паспорте на образцовую меру.

Анализ результатов исследования позволил сделать следующие выводы:

- методом трех вольтметров довольно просто измерять составляющие индуктивного импеданса на фиксированных частотах до 100 кГц, при этом относительная погрешность определения индуктивности составляет не более 0,3%, активного сопротивления – 8,65%, что соответствует классу точности использованных измерительных приборов;

- метод дает возможность получать информативную характеристику в виде частотной зависимости составляющих индуктивного импеданса; это позволяет выбрать диапазон частот, в котором мешающее влияние распределенной емкости незначительное, а также найти оптимальную частоту, при которой добротность индуктивности максимальна;

- дальнейшее повышение точности определения действительного значения индуктивности возможно при условии проведения анализа эквивалентной схемы измерительной цепи, учитывающей шунтирующее влияние распределенной емкости.

Литература:

1. Измерения в электронике: Справочник / В.А. Кузнецов, В.А. Долгов, В.М. Колесник и др.; Под ред. В.А. Кузнецова. – М.: Энергоатомиздат, 1987. – 512 с.

2. Круг К.А. Основы электротехники.Теория переменных токов. – М.-Л.: Государственное энергетическое издательство, 1946. – 635 с.