Мельник В.Н., Карачун В.В.
Национальный технический университет Украины «КПИ»
ВЫБОР КОРРЕКТИРУЮЩИХ ФУНКЦИЙ ПРИ АНТИСИММЕТРИЧНОМ
ДЕФОРМИРОВАНИИ
ПОПЛАВКОВОГО ПОДВЕСА
Примем вначале, что
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Полагаем, что координатные функции подвеса имеют вид [1]:
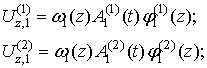 (4)
(4)
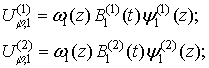 (5)
(5)
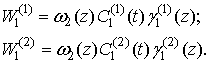 (6)
(6)
Выбираем
следующие представления функций Кравчука:
![]() (7)
(7)
![]() (8)
(8)
Пусть имеются произвольные соотношения вида:
![]()
![]()
где ![]() произвольные
дифференцируемые функции.
произвольные
дифференцируемые функции.
Вычислим следующие производные:
![]()
![]() (9)
(9)
Так как
![]()
тогда
![]()
Продифференцируем это выражение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (10)
(10)
Положив
в (9) и (10) ![]() ,
, ![]() , приходим к выводу, что
, приходим к выводу, что
![]()
Проверяем, равна ли нулю третья производная ![]() Для этого
используем формулу (10). Получаем
Для этого
используем формулу (10). Получаем
![]() (11)
(11)
Проверяем вторую производную ![]()
![]()
![]() (12)
(12)
Вычисляем
![]() при
при ![]() и
и ![]() :
:
![]()
Принимая во внимание соотношения (9), (11) и (12) приходим к выводу, что
аппроксимации (1) - (3) удовлетворяют любым граничным условиям с точностью до
перемещений оболочки как абсолютно твердого тела.
Строго говоря, на краях будут иметь место какие-то перемещения, но
вследствие значительной жесткости выпуклой (вогнутой) оболочки ими можно
пренебречь по сравнению с перемещениями абсолютно твердой оболочки.
Теперь, для определения отыскиваемых функций
![]()
![]()
![]()
можно
применить метод Бубнова-Галеркина.
Итак, представим соотношения (4 - 6) представим в виде:
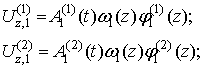 (13)
(13)
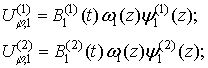 (14)
(14)
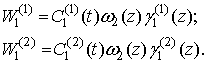 (15)
(15)
Литература:
1. Карачун
В.В, Мельник В.М., Ковалец О.Я. Линейно-упругий поплавковый подвес гироскопа. –
К.: «Корнейчук», 2009. -240 с.