Ковалец О.Я.

Национальный технический университет Украины «КПИ»

ОПРЕДЕЛЕНИЕ ЧАСТОТ ПОПЛАВКОВОГО ПОДВЕСА КАНОНИЧЕСКОЙ ФОРМЫ

Чтобы получить уравнение частот для трех пар дифференциальных уравнений, формально примем равными нулю их правые части:

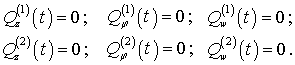(1)

Затем, используем аппроксимации вида

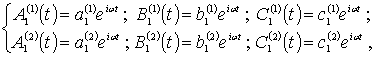(2)

где – произвольные постоянные, для подстановки в уравнения движения. Получаем:

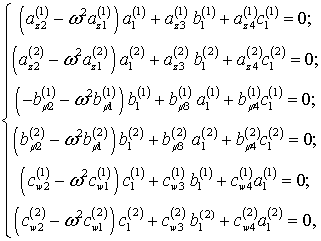(3)

Система уравнений (3) распадается на две независимых:

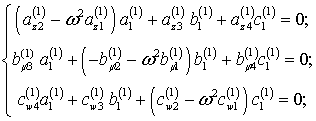(4)

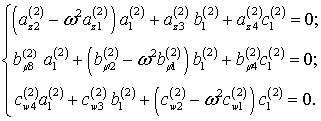(5)

Или в таком виде:

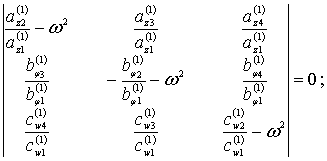(6)

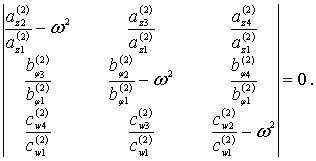(7)

Соотношения (6), (7) дают возможность определить частоты . Из выражения (3) получаем:

(8)

где

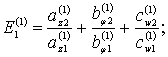
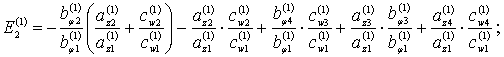
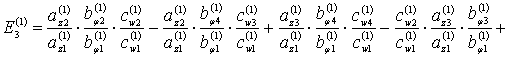
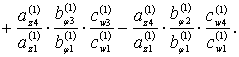
Аналогично, из (7) получаем второе уравнение частот:

(9)

где

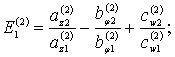
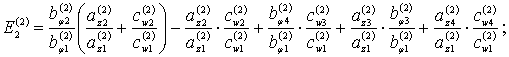
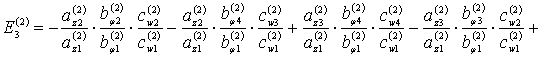
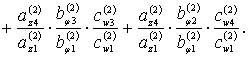
Перейдем от канонической формы записи уравнений (8) и (9) к виду, удобному для отыскания корней кубического уравнения. Имеем, соответственно:

(10)

где

(11)

где

В обоих уравнениях дискриминант , что позволяет сделать вывод о наличии одного положительного корня как в формуле (10), так и в выражении (11). Два других корня – комплексные.

Тогда, применив формулу Кардана для уравнений (10) и (11), находим решение в виде

(12)

где

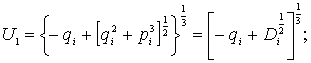
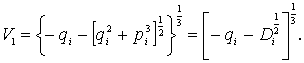(13)

Численный анализ в режиме вычислительных операций MATCHAD позволяет найти значения собственных частот поплавка (табл. 1).

Таблица 1

Частоты собственных колебаний поплавкового подвеса гироскопа канонической формы

δ	ω	ω
0	1,404	1,183

Таким образом, для поплавка в виде классического кругового цилиндра с нулевой кривизной боковой поверхности , имеют место две собственные частоты: и .