Ñîâðåìåííûå èíôîðìàöèîííûå
òåõíîëîãèè/1. Êîìïüþòåðíàÿ èíæåíåðèÿ
cand. tech.
sci. Semakhin A.M.
Kurgan State University, Russia
METHOD GOMORY IN THE DECISION OF THE INTEGER PROBLEM
OF OPTIMIZATION OF INFORMATION SYSTEM
Integer linear programming is focused on the decision of problems of
linear programming in which all or some variables accept integer values /1/.
For the decision of
an integer task of linear programming Ralph E. Gomory has offered the
cutting-plane method in 1958 /2/.
The Gomory’s
algorithm contains stages:
The stage 1. The
integrity is ignored, the simplex method is found the optimum plan. If the
decision fractional transition to 2 stage.
Stage 2. The
decision of the expanded problem /2/.
Let's develop
integer mathematical model of information system and we shall define the
optimum decision by cutting-plane method.
The mathematical
model is formulated as follows: from among the firms, rendering services
satellite Internet in territory of the Russian Federation, it is required to
choose the provider satellite Internet with the maximal size of the pure
resulted effect (NPV) and satisfying to financial restrictions /3/.
Let 
- share of financing
of the project NTV-plus, 
- share of financing
of project Europe On Line, 
- share of financing
of project Astra Network, 
- share of financing
of project Satpro, 
- share of financing
of project Network Service. 
- binary variables.
The integer
mathematical model looks like
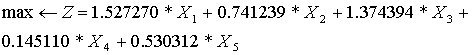
subject to
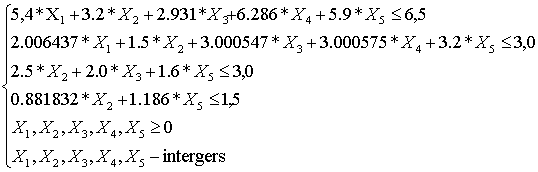
Let's solve a
continuous problem. We shall lead to the standard form and we shall make the
initial Jordan’s table (table 1).
Table 1
The initial
Jordan’s table
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
6.5 |
5.4 |
3.2 |
2.931 |
6.286 |
5.9 |
|
|
3.0 |
2.006437 |
1.5 |
3.000547 |
3.000575 |
3.2 |
|
|
3.0 |
0.0 |
2.5 |
2.0 |
0.0 |
1.6 |
|
|
1.5 |
0.0 |
0.881832 |
0.0 |
0.0 |
1.186 |
|
Z= |
0 |
-1.52727 |
-0.741239 |
-1.374394 |
-0.14511 |
-0.530312 |
=
=
=
=
The first iteration
is resulted in table 2.
Table 2
The first iteration
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
0,58484 |
-0,371563 |
0,311 |
1,911498 |
0,664934 |
1,007782 |
|
|
3,0 |
0 |
2,5 |
2,0 |
0 |
1,6 |
|
|
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
Z= |
1,83838 |
0,282827 |
0,16381 |
-0,545426 |
1,632745 |
1,138371 |
=
=
=
=
The optimum
decision of a continuous problem is resulted in table 3.
Transition to the
second stage of Gomory’s algorithm.
The basic variable
gets out 
with the greatest
fractional part: 
, 
, 
. The equation is worked out for variable 
.
The expanded
problem and the third iteration are presented in table 4 and table 5.
Table 3
The optimum decision of a continuous problem. The second iteration
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
1,037635 |
0,290692 |
0,504283 |
-0,283954 |
0,975263 |
0,806429 |
|
|
0,305961 |
-0,194383 |
0,1627 |
0,52315 |
0,34786 |
0,527221 |
|
|
2,388078 |
0,388766 |
2,174601 |
-1,0463 |
-0,69572 |
0,545558 |
|
|
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
Z= |
2,00526 |
0,176807 |
0,252551 |
0,28534 |
1,822477 |
1,425931 |
=
=
=
=
Table 4
The expanded problem with the first additional restriction
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
1,037635 |
0,290692 |
0,504283 |
-0,283954 |
0,975263 |
0,806429 |
|
|
0,305961 |
-0,194383 |
0,1627 |
0,52315 |
0,34786 |
0,527221 |
|
|
2,388078 |
0,388766 |
2,174601 |
-1,0463 |
-0,69572 |
0,545558 |
|
|
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
|
-0,305961 |
0,194383 |
-0,1627 |
-0,52315 |
-0,34786 |
-0,527221 |
|
Z= |
2,00526 |
0,176807 |
0,252551 |
0,28534 |
1,822477 |
1,425931 |
=
=
=
=
=
The optimum
nonintegral decision is resulted in table 6.
The expanded
problem with the second additional restriction is presented in table 7.
The fifth iteration
is resulted in table 8
The expanded
problem and the optimum integer decision are presented in table 9 and table 10.
The optimum integer plan 
=
is presented in table 10. Value of criterion function is
equaled 1.52727.
Table 5
The third iteration
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
0,569642 |
0,588017 |
0,25542 |
-1,084156 |
0,443182 |
1,529584 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
2,071475 |
0,58991 |
2,006242 |
-1,587645 |
-1,055679 |
1,034781 |
|
|
0,811731 |
0,437271 |
0,515833 |
-1,176842 |
-0,782522 |
2,249531 |
|
|
0580328 |
-0,368694 |
0,308599 |
0,992278 |
0,659799 |
-1,896738 |
|
Z= |
1,177753 |
0,702539 |
-0,18749 |
-1,129581 |
0,881649 |
2,704617 |
=
=
=
=
=
Table 6
The optimum nonintegral decision. The
fourth iteration
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
1,203704 |
0,185185 |
0,592593 |
1,09259 |
1,164074 |
-0,542779 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
3 |
0 |
2,5 |
1,6 |
0 |
-2 |
|
|
1,5 |
0 |
0,881832 |
1,186 |
0 |
0 |
|
|
0,584844 |
-0,371563 |
0,311001 |
1,007782 |
0,664934 |
-1,911499 |
|
Z= |
1,838386 |
0,282829 |
0,16381 |
1,13837 |
1,632745 |
0,545424 |
=
=
=
=
=
Table 7
The expanded problem with the second additional restriction
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
1,203704 |
0,185185 |
0,592593 |
1,09259 |
1,164074 |
-0,542779 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
3 |
0 |
2,5 |
1,6 |
0 |
-2 |
|
|
1,5 |
0 |
0,881832 |
1,186 |
0 |
0 |
|
|
0,584844 |
-0,371563 |
0,311001 |
1,007782 |
0,664934 |
-1,911499 |
|
|
-0,203704 |
-0,185185 |
-0,592593 |
-0,09259 |
-0,164074 |
0,542779 |
|
Z= |
1,838386 |
0,282829 |
0,16381 |
1,13837 |
1,632745 |
0,545424 |
=
=
=
=
=
= Table 8
Cutting off of a
fractional part of variable 
. The fifth iteration
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
2,14062 |
-0,781249 |
4,21875 |
1,20939 |
-0,692187 |
0,289847 |
|
|
1,19687 |
-0,275572 |
1,48809 |
1,04822 |
-0,244157 |
0,807704 |
|
|
0,477937 |
-0,468751 |
0,524814 |
0,959189 |
0,578826 |
-1,62664 |
|
|
0,34375 |
0,312499 |
-1,6875 |
0,156246 |
0,276875 |
-0,915939 |
|
Z= |
1,78208 |
0,231638 |
0,276429 |
1,11278 |
1,58739 |
0,695464 |
=
=
=
=
=
=
Table 9
The expanded problem with the third additional restriction
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
2,14062 |
-0,781249 |
4,21875 |
1,20939 |
-0,692187 |
0,289847 |
|
|
1,19687 |
-0,275572 |
1,48809 |
1,04822 |
-0,244157 |
0,807704 |
|
|
0,477937 |
-0,468751 |
0,524814 |
0,959189 |
0,578826 |
-1,62664 |
|
|
0,34375 |
0,312499 |
-1,6875 |
0,156246 |
0,276875 |
-0,915939 |
|
|
-0,34375 |
-0,312499 |
0,68785 |
-0,156246 |
-0,276875 |
0,915939 |
|
Z= |
1,78208 |
0,231638 |
0,276429 |
1,11278 |
1,58739 |
0,695464 |
=
=
=
=
=
=
=
Results of the lead
researches have allowed to draw following conclusions.
1. The integer
mathematical model of optimization of the information system is developed,
allowing to reduce expenses and terms of designing of information systems and
to raise validity of accepted decisions.
2. The optimum
decision of an integer problem of optimization of information system is found
by the cutting-plane method. For a finding of the integer optimum plan six
iterations are executed and three additional restrictions are entered.
Table 10
The optimum integer decision. The sixth iteration
|
ÁÏ |
1 |
- |
- |
- |
- |
- |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
3 |
-2,5 |
2,5 |
1,60001 |
0 |
-2 |
|
|
1,5 |
-0,881833 |
0,88183 |
1,186 |
0 |
0 |
|
|
0,993565 |
-1,50001 |
-0,506442 |
1,19356 |
0,994141 |
-3,00056 |
|
|
0 |
1 |
-1 |
0 |
0 |
0 |
|
|
1,1 |
-3,20001 |
-2,20001 |
0,499989 |
0,886003 |
-2,93101 |
|
Z= |
1,52727 |
0,741244 |
0,786034 |
0,996964 |
1,38216 |
1,3744 |
=
=
=
=
=
=
=
References:
1. Hamdy A Taha
Operations Research: An Introduction. Seven Edition - Ì.: Publishing house "Williams", 2005 - 912
p.
2. Êînuhovski P. V. Mathematical methods of research of
operations in economy. – SPb.: Publishing house " Peter ", 2000. -
208 p.
3. Semakhin A.M.
The analysis of mathematical model of information system. In the collection of
materials X of the All-Russia scientifically-practical conference with the
international participation (on November, 25-26th, 2011). - Tomsk: : Publishing
house of Tomsk university . Part 2 - 206 p.