Математика 3/. Числа Каталана

Жумиров Б. А., Жумирова Ж. Ж.

Магистрант Инновационного Евразийского университета, Казахстан

Числа Каталана в теории вероятности

         Числа Каталана — числовая последовательность, встречающаяся в удивительном числе комбинаторных задач. Эта последовательность названа в честь бельгийского математика Каталана, жившего в 19 веке.

Первые несколько чисел Каталана   (начиная с нулевого):

1,  1,  2,  5,  14,  42,  132,  429,  1430......

         Числа Каталана встречаются в большом количестве задач комбинаторики. Имеется две формулы для чисел Каталана: рекуррентная и аналитическая.

         Аналитическая формула: , здесь через  обозначен, как обычно, биномиальный коэффициент.

Задача о человеке в казино

         Немного подумав, мы придумали задачу, которая включает числа Каталана и теорию вероятностей и надеемся, что решение таких видов задач понадобятся для решения аналогичных задач в разных сферах математики.

Задача:

         Человек пришел в казино с одним долларом. Ставки в казино равны одному доллару. И вероятность выигрыша и проигрыша 50 на 50. При выигрыше дается один доллар, при проигрыше же отнимается. Подсчитать вероятность того, что человек через n количество ставок будет оставаться при деньгах (т. е. его деньги не будут равняться нулю, иначе он не сможет играть дальше).

Решение: Очевидно, что при , у него вероятность, либо выиграет, либо проиграет.

         Известна формула вероятностей:  .

         Где P(A) = количество успешных событий, а P(U) = количество всех событий. Очевидно, что P(U) при определенных n равно , то есть, в каждой игре есть по два варианта либо выиграет, либо проиграет. Далее, мы будем подсчитывать P(A) для определенных n. Выразим выигрышей через +, а проигрышей .

         Итак, подсчитаем P(A) для определенных n.  Поначалу, подсчитаем собственноручно для малых значений.

         Логика следующих вычислений такова, исход первой игры не может быть минусом, потому что при противном он будет без денег уже при первой игре. И количество минусов не должно превысить плюсы, потому что при обратном у человека не останеться денег. Для 2 игр получим следующие правильные результаты при котором человек будет оставаться при деньгах:

1)++;   2)+-

Для 3 игр получим следующие результаты:

1)+++;   2)++-;   3)+-+

Для 4 игр получим следующие результаты:

1)++++; 2)+++-;  3)++-+;   4)+-++;   5)++--;  6)+-+-

Для 5 игр получим следующие результаты:

1)+++++;  2)++++-;   3)+++-+;   4)++-++;   5)+-+++;   6)+++--;  7)++-+-;   8)++--+; 9)+-++-;   10)+-+-+.

         Как понятно, при нечетном количестве игр количество плюсов всегда на один превышает минусов. Так что в следующем ряду с каждого крайнего элемента потянуться два варианта, и это значить, что количество вариантов умножиться на два. Следовательно, .

         А как поведет себя ряды когда будут переходит с четного на нечетное?

При четном количестве, очевидно что два варианта выйдут с тех вариантов в котором количество плюсов больше, чем количество минусов. А с тех вариантов, где количество плюсов равно минусам потянется один вариант на (+), потому что при обратном, если потянется к (-), то количества минусов станет на один больше чем количества плюсов. А это не соответсвует условию, у человека больше проигрышей чем выигрышей, и это светит банкротом.

         Значит, , где  А - является количеством вариантов при одинаковых количествах выигрышей и проигрышей. Теперь нам надо подсчитать их.

Рассмотрим для .

Существует единственный вариант:

1)    +-

Рассмотрим для .

1)    ++--;  2) +-+-.    Как видим, существует два варианта.

Рассмотрим для .

1)    +++---;   2)++-+--;   3) ++--+-;  4) +-++--;  5)+-+-+-.

Существует 5 вариантов.

И тут можно заметить что «+» и «–»  подобны расстановкам правильных скобок.  И тут определяем что для   будет С4 – четвертое число Каталана – 14. Для  будет 42,   для  будет 132 и т.д. Следовательно в выражений    ,    X  равняется Сn - n-ое число Каталана.

         Далее можно вывести следующий алгоритм и получить формулу через сумму:

..................................       

 

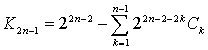
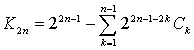
Cледовательно: 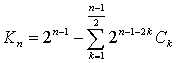, где -  это количество вариантов при которых игрок  остаётся в казино,  числа Каталана и [f(x)] – является целым значением от f(x).

         Теперь подсчитав количество вариантов мы можем легко подсчитывать вероятности для маленьких значений n. Но можем определить и для больших n при помощи разных языков программирования.

         Например:

Подсчитаем  какова вероятность оставаться при деньгах после пяти игр?

         Решение:

Примерно 31.25% вероятности остаться в казино с деньгами.   

         Еще примеры:

Подсчитаем  какова вероятность оставаться при деньгах после десяти игр?

         Решение:

Примерно 24.61% вероятности что человек останется в казино.

Мы можем решать аналогичные задания с использованием данной формулы. Мы будем продолжать исследование в этой сфере и хотим выявить использование чисел Каталана еще в разных сферах.

         Заключение: используя формулы чисел Каталана, можно решить более трудные задачи по алгебре.

Литература:

1.     www.problems.ru

2.     www.acmp.ru

3.     e-maxx.ru/algo/catalan_numbers

4.      Дискретная Математика и комбинаторика. Дж. Андерсон 2003 г.