Редькина Татьяна Валентиновна

Ставропольский государственный университет, Россия

Использование потенциалов Баргмана для построения

точных решений

Как показано в [1], используя одномерный оператор Дирака и операторное уравнение Лакса, можно построить нелинейное уравнение

(1)

Построим точные решения для этого уравнения.

ТЕОРЕМА 1. Нелинейное уравнение (1), обладающие парой Лакса с оператором рассеяния Дирака, имеет следующие решения: , , , где , , - произвольная функция, - произвольный параметр.

Рассмотрим матричное уравнение Дирака, связанное с уравнением (1)

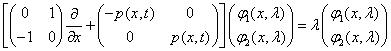. (2)

Исходным пунктом метода Баргмана является предположение, состоящее в том, что существуют потенциалы уравнения (2) такие, что решения этого уравнения могут быть записаны в виде

, (3)

где являются полиномом от и параметрически зависит от t, так как в системе (2) предполагается параметрическая зависимость потенциала от t. Простейшим нетривиальным примером является линейная форма

, (4)

где вид функций и значение постоянных уточняется в дальнейшем. Подставляя решение (3) в систему уравнений (2), сокращая на , и приравнивая члены с одинаковыми степенями , получим систему

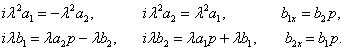(5)

Как видно из (5) первые и последние пары дают соотношения

, (6)

где – постоянная интегрирования выбрана в таком виде для удобства дальнейших преобразований, она может быть взята с разными знаками и даже может обращаться в нуль. Подстановка (6) приводит систему к виду

(7)

– постоянная интегрирования.

I. Простейший случай, когда в , тогда решением уравнения (1) будет функция . Подстановка этого значения в уравнение (1) показывает, что равенство выполняется тождественно и функция остается произвольной.

II. Вторая возможность, которая может дать новый вид решения возникает, если положить в . Выполним некоторые преобразования и проинтегрируем (7)

, (8)

где , - произвольная функция. Выполним подстановку найденной функции в (6), тогда найдем

и , (9)

где . Аналогично случаю I доопределим произвольные функции , используя подстановку полученного вида функции (9) в уравнение (1), что дает , а на функцию никаких дополнительных ограничений не наложено и функция осталась произвольной. В результате мы получаем точное решение уравнения (1) в виде .

Предполагая, что системы (3) имеют вид

, (10)

где имеют квадратичный вид относительно Подстановка этого выражения в систему Дирака (2) дает несколько условий

(11)

Положим в системе (11) , , , - произвольная функция. Оставшиеся четыре уравнения системы (11) связывают только функции

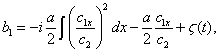(12)

где - произвольная функция. В результате осталось неразрешенным только одно интегро-дифференциальное уравнение

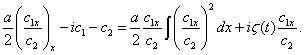(13)

Вводя в (13) следующую подстановку

, , , (14)

приведем его к виду

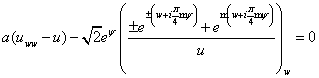. (15)

Его частное решение , после подстановки (14) в (1) и уточнения функции , дает решение .

Литература

1.Редькина Т.В. Нелинейное уравнение, связанное с оператором Дирака//Materiály VIII mezinárodní vědecko – praktická Konference «Dny Vědy – 2012». Díl 82 Matematika. Praha. Publishing House «Education and Science» s.r.o. 2012. 8-11. 96 stran.