Лямина О.С.

Забайкальский государственный университет, Россия

О связи между константами и .

Тригонометрические операторы Баскакова – это совокупность аппроксимирующих последовательностей операторов, определенных на множестве суммируемых периодических функций. Эти операторы определяются формулой:

,

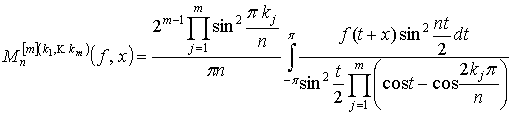где целые параметры m, k_j не зависят от n и удовлетворяют неравенствам .

Известно, что если , то

где 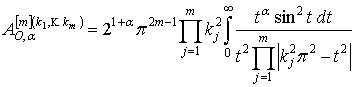(говорят, что принадлежит классу , если выполняется ).

Теорема 2.6. При каждом и при любом зафиксированном выполняется предельное равенство =.

Доказательство. Обозначим

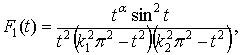
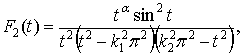
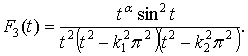
Получаем

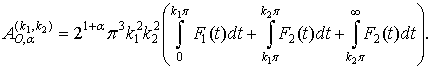(1)

Таким образом представлено суммой трех слагаемых. Рассмотрим отдельно каждое слагаемое.

Проанализируем первое слагаемое правой части равенства (1)

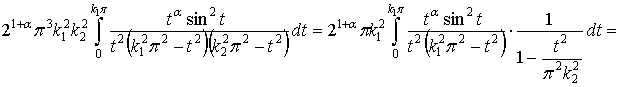
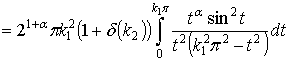, при этом .

Следовательно,

.

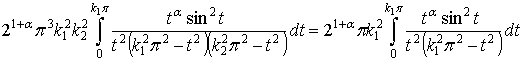Для анализа второго слагаемого правой части равенства (1) рассмотрим разность

.

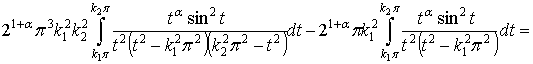
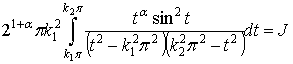Так как 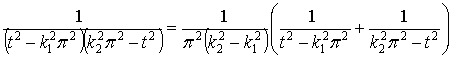, имеем

.

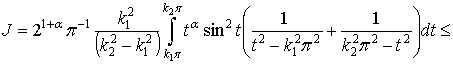
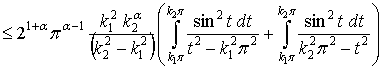Множитель 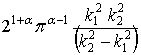представляет собой бесконечно малую при . Исследуем интегралы в скобках.

Преобразуем и оценим первый из них

==.

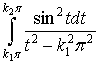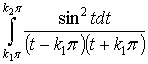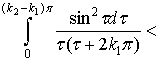
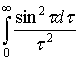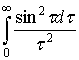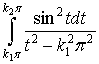Интеграл сходится, следовательно интеграл равномерно по ограничен.

Оценим второй интеграл.

< .

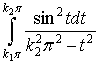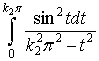Последний интеграл равномерно по ограничен.

Итак,

.

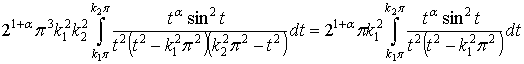Так как 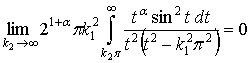, то для того, чтобы закончить доказательство теоремы достаточно показать, что

.

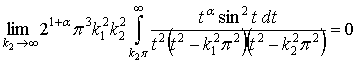Имея в виду 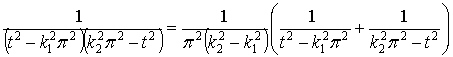, получаем

.

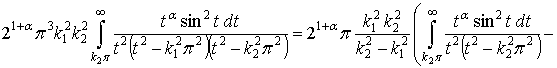
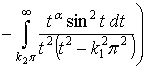Множитель 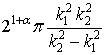величина (относительно ) ограниченная. Далее, подынтегральное выражение 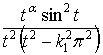сходящегося интеграла 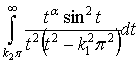от не зависит. Следовательно, .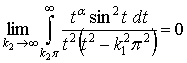

Рассмотрим теперь интеграл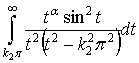 (первый интеграл в скобках)

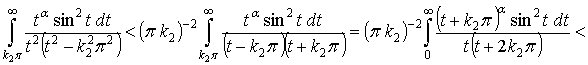
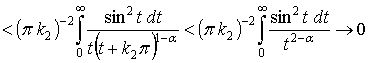при .

Теорема доказана.