Метод исследования устойчивости нелинейных автономных динамических систем без применения функции Ляпунова.

К настоящему времени исследование устойчивости нелинейных динамических систем с сосредоточенными параметрами, описываемых обыкновенными дифференциальными уравнениями или интегральными уравнениями Вольтерра второго рода, сводимыми к системам уравнений с обыкновенными производными, а также нелинейных динамических систем, описываемых дифференциальными уравнениями с частными производными, опирается на фундаментальные теоремы Ляпунова об устойчивости по первому приближению, на векторные функции Ляпунова, на качественную теорию Пуанкаре и на теорию Колмогорова об устойчивости систем с гамильтонианом при малых колебаниях.

Однако для построения функции Ляпунова не имеется общего алгоритма - известны лишь частные приемы эвристического ее задания, качественная теория требует выявления точек покоя (узел, седло, фокус, центр), что эффективно реализуемо лишь при исследовании двумерных динамических систем, а метод линеаризации в общем случае не приводит к полным и правильным результатам.

Поэтому существует актуальная необходимость исследования устойчивости нелинейных динамических систем без построения функций Ляпунова, без линеаризации систем и без применения качественной теории.

Аналогичное обстоятельство имеет место и при исследовании структурной устойчивости нелинейных динамических систем, так как к настоящему времени в основу ее исследований принимается потенциальная функция, которую, как известно, можно построить только для потенциальных систем.

Сущность настоящей работы заключается в изложении метода и алгоритма вывода необходимых и достаточных условий динамической и структурной устойчивости нелинейных не потенциальных и потенциальных автономных динамических систем с сосредоточенными и распределенными параметрами.

Основу метода составляют теоремы, опубликованные авторами в [1] о

- существовании сопряженной линейной гамильтоновой системы с функциональными коэффициентами для любой исходной автономной нелинейной системы дифференциальных уравнений, описывающих исследуемую нелинейную систему, а также для систем нелинейных дифференциальных уравнений, полученных при соответствующем преобразовании интегрального уравнения Вольтерра второго рода или в результате преобразования нелинейных уравнений с частными производными оператором Фурье-Лапласа;

- обосновании критериев асимптотической устойчивости нелинейной автономной системы;

- обосновании критериев структурной устойчивости нелинейной автономной системы.

Согласно этим теоремам построен алгоритм формирования искомых необходимых и достаточных условий динамической и структурной устойчивости, алгоритм опубликован в [2].

Применим эти теоремы для исследования конкретных систем.

1. Исследуем устойчивость решения системы нелинейных дифференциальных уравнений Еругина-Айзермана (проблемы Еругина-Айзермана)

, (1)

где - нелинейная функция.

Для этого построим сопряженную к (1) систему:

, ,

выпишем для нее характеристическое уравнение

и составим главные диагональные миноры Гурвица

, , .

Из последних сформируем необходимые и достаточные условия асимптотической устойчивости решения системы (1)

, (2)

=> . (3)

Докажем, что полученные условия полностью охватывают принятые в [3] допущения для устойчивости решения системы (1). Они записаны в [3] в виде

, (4)

(5)

во всех случаях кроме одного, когда

, или . (6)

Действительно, условия неустойчивости системы (1) являются следствием отрицания полученного предложенным методом необходимого и достаточного условия (5), то есть следствием неравенства

или, что то же, следствием неравенства

.

Из таких выражений-неравенств видно, что функция при отрицательна и убывает, поэтому

,

а при функция положительна и убывает, поэтому

,

что однозначно воспроизводит условия (6). Теперь, воспользовавшись условиями неустойчивости

,

решения системы (1), получаем очевидным образом условие .

Доказательство завершено.

2. Проведем исследование структурной устойчивости системы конкурирующих популяций, описываемой системой нелинейных дифференциальных уравнений

, (7)

где , , , , , .

С этой целью выявим точки бифуркации решения системы (7).

Для этого составим сопряженную гамильтонову систему по отношению к исходной нелинейной системы и выпишем для нее характеристическое уравнение. Последнее имеет вид:

,

где - собственное значение матрицы правой части сопряженной системы.

По одной из доказанных авторами теорем [4] точкам бифуркации соответствуют точки разрыва собственного значения как функций от параметров , , , , , . Такие зависимости строятся с использованием систем символьной математики [7]. На рисунке 1 представлена зависимость собственного значения от параметров , при фиксированных значениях других параметров , , , . Видно, что имеет место скачкообразное изменения собственного значения при равенстве параметров и .

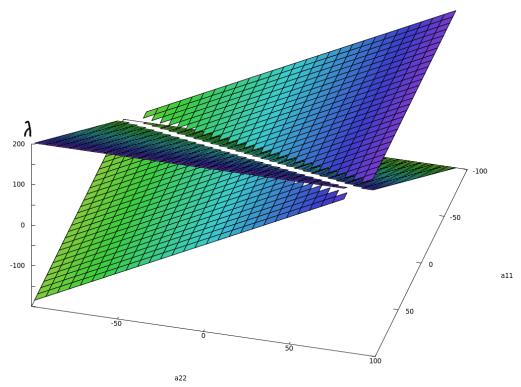
Рис. 1.

Из анализа установленных зависимостей следует, что разрыв действительной части возникает при ; бифуркации отсутствуют при неодинаковых значениях и . Установлена также возможность прогнозирования возникновения бифуркаций решения системы конкурирующих популяций.

Отметим, что таким образом математически обосновано, что конкурирующие популяции с одинаковыми коэффициентами саморегуляции роста не могут сосуществовать в одном месте обитания. Отметим также, что Вольтерра [5] доказал этот факт (как принцип Гаузе) при сведении исследуемой системы к линейному уравнению первого порядка, разрешенному относительно производной , когда в правых частях одна и та же нелинейность, то есть в частном случае описания взаимодействия конкурирующих систем. Предложенный авторами метод свободен от такого рода допущений.

3. Проведем исследование динамической системы, описываемой нелинейной системой дифференциальных уравнений с частными производными:

, (8)

где - вектор фазовых координат, - неизвестная функция, - нелинейная функция.

Для этого подействуем на уравнение (8) преобразованием Фурье по каждой переменной, получим дифференциальное уравнение вида

,

Этому уравнению однозначно соответствует нелинейная система обыкновенных дифференциальных уравнений. Запишем ее в векторной форме:

, (9)

где - нелинейная вектор-функция. Затем для этой системы построим гамильтонову сопряженную систему:

,

где , и выпишем для последней характеристическое уравнение вида [6]:

, (10)

где - сумма главных миноров - го порядка матрицы сопряженной системы.

Теперь по (10) можно составить необходимые и достаточные условия для устойчивости решения системы (9), а затем воспользоваться теоремой Планшереля [3]. В соответствии с теоремой Планшереля, норма решения уравнения (8) в исходном пространстве равна норме решения уравнения (9) в пространстве Фурье-образов над полем комплексных чисел:

=,

но тогда при

,

выполняется

, ,

то есть при асимптотической устойчивости решения (9) асимптотически устойчиво и решение (8), и наоборот.

Заключение. Разработанный метод применим для исследования динамической и структурной устойчивости различных нелинейных автономных систем с гладкими нелинейностями и для таких систем он, в отличие от известных методов, не требует введения функции Ляпунова и потенциальной функции.

Литература.

1. Катулев А.Н., Кузнецов А.Ю., Исследование устойчивости нелинейных автономных динамических систем без применения функции Ляпунова//Вестник ТвГУ. Серия: прикладная математика, №35, 2011, с.75.

2. Катулев А.Н., Кузнецов А.Ю., Алгоритм исследования устойчивости решений нелинейных автономных систем дифференциальных уравнений//Нелинейный мир, №10, т.8, 2010, с.616.

3. Бойков И.В. Устойчивость решений дифференциальных уравнений. Издательство Пензенского государственного университета, Пенза, 2008.

4. Катулев А.Н., Кузнецов А.Ю., Исследование устойчивости автономных нелинейных динамических систем// Труды МАИ, т.28, 2010.

5. Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976.

6. Гантмахер Ф.Р. Лекции по аналитической механике. М.: Физматлит, 2001.

7. Кузнецов А.Ю., Программный комплекс для исследования устойчивости нелинейных динамических систем//Программные продукты и системы, №1, 2012, с.15.