Технические науки / 6. Электротехника и радиоэлектроника

К.т.н. Сухарьков О.В.

Одесская национальная академия связи им. А.С. Попова, Украина

Динамика изгибных автоколебаний плоской осесимметричной струи

Разработка и исследование длинноволновых излучающих антенн дальней связи является важной проблемой информационной гидроакустики. В качестве основных элементов таких антенн перспективно использовать низкочастотные (0,3…6) кГц жидкоструйные излучатели с кольцевым соплом и ступенчатым препятствием [1]. Для модифицированного жидкоструйного преобразователя c круговым щелевым соплом в виде соосных дисков предложена физическая модель на основе изгибных автоколебаний упругой затопленной кольцевой струйной пластинки при наличии развитой кавитации [2]. Настоящий доклад посвящен решению задачи собственных колебаний затопленной плоской осесимметричной струи.

Рассмотрим возможный механизм генерации звука модифицированным жидкоструйным излучателем (рис. 1, а).

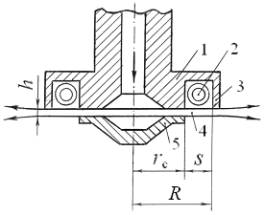
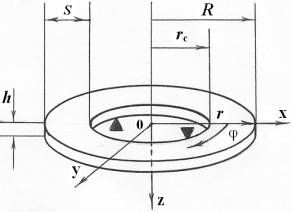
а) б)

Рисунок 1 – Модифицированный жидкоструйный преобразователь: а – схема, б – модель кольцевой струйной пластинки

Затопленная струя, вытекающая из кругового щелевого сопла, образованного соосными дисками корпуса 1 и обтекателя 5, формируется в плоскую осесимметричную струю 4 в форме кольцевой пластинки. Ступенчатое препятствие 3 способствует тому, что часть кинетической энергии струи расходуется на формирование в проточке корпуса 1 тороидального вихря 2, внутри которого за счет эффекта Бернулли возникает кавитация. Пульсации вихря 2 возбуждают вертикальные изгибные колебания кольцевой струйной пластинки. Оптимальный режим гидродинамического звукообразования, при котором генерируется акустический сигнал максимального уровня, соответствует совпадению частоты пульсаций вихря с частотой основной гармоники колебаний кольцевой пластинки [2].

Кольцевая струйная пластинка характеризуется геометрическими параметрами: толщиной , шириной , внутренним радиусом и внешним радиусом (рис. 1, б). Причем толщина пластинки мала по сравнению с радиусом . Расположим оси и в верхней плоскости кольцевой пластинки, ось направим по нормали к этой плоскости, и декартову систему координат совместим с цилиндрической системой координат. В первом приближении струйную пластинку можно рассматривать как твердотельную с некоторым эквивалентным модулем упругости. Для определения частоты собственных колебаний кольцевой струйной пластинки воспользуемся однородным дифференциальным уравнением изгиба круглой пластинки в полярных координатах [3]

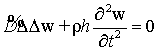, (1)

где 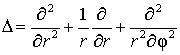– оператор Лапласа;– динамический прогиб пластинки; – параметр времени; – плотность материала струйной пластинки; – цилиндрическая жесткость кольцевой пластинки.

Ввиду радиальной симметрии изгибные колебания кольцевой пластинки естественно считать независящими от угловой координаты . Перейдем от переменной к приведенному расстоянию и учтем, что (рис. 1, б). Тогда, используя метод разделения переменных Фурье в уравнении (1), для определения формы колебаний струйной кольцевой пластинки получим дифференциальное уравнение [4]

, (2)

где 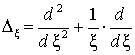. При этом для характеристического параметра справедливо выражение

, (3)

где – круговая частота колебаний. В связи с тем, что материалом пластинки является жидкость и пластинка, испытывающая колебания, находится в затопленном состоянии в этой же жидкости, то коэффициент Пуассона [5]. Это позволяет для вычисления коэффициента жесткости кольцевой пластинки использовать формулу

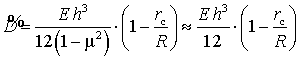, (4)

где – эквивалентный модуль упругости затопленной плоской струи.

Общее решение дифференциального уравнения (2) имеет вид [4]

, (5)

где – функция Бесселя первого рода 0-го порядка; – функция Бесселя второго рода 0-го порядка; – модифицированная функция Бесселя первого рода 0-го порядка; – модифицированная функция Бесселя второго рода 0-го порядка [6].

Согласно предложенной модели считаем, что внутренний край струйной кольцевой пластинки жестко защемлен, а на наружном крае – отсутствуют продольное смещение, сдвиг и перерезывающие усилия [3]. Тогда граничные условия на контурах пластинки запишем в виде:

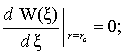
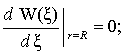
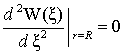. (6)

Неизвестные в решении (5) коэффициенты можно определить из соотношений, получаемых из граничных условий (6), путем их алгебраизации. Характеристические параметры , входящие в уравнение колебаний кольцевой пластинки, являются корнями трансцендентного уравнения [4]:

(7)

При этом частоте основного тона (низшая гармоника) генерируемого акустического сигнала соответствует первый корень уравнения (7) [7]. Тогда, используя выражения (3) и (4), получим формулу для расчета частоты основной гармоники жидкоструйного излучателя с круговым щелевым соплом в виде соосных дисков

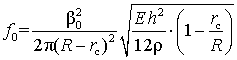. (8)

Для проверки соответствия предложенной математической модели параметрам реального устройства в акустическом бассейне исследовались частотные характеристики пяти излучателей, у которых радиус сопла принимал значения: мм (рис. 1). Исследования показали, что все испытуемые жидкоструйные излучатели начинают генерировать тональный акустический сигнал при ширине кольцевой струйной пластинки мм. На рис. 2 для трех излучателей представлена зависимость частоты основного тона сигнала от относительной ширины кольцевой пластинки в диапазоне значений . Здесь точки соответствуют экспериментальным измерениям частоты основной гармоники генерируемого сигнала, сплошные линии – результаты расчета по формуле (8).

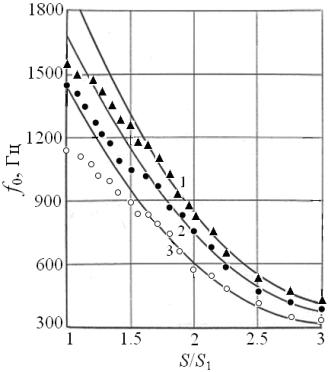
Рисунок 2 – Зависимость частоты основной гармоники звукового сигнала от относительной ширины кольцевой струйной пластинки: 1 – мм; 2 – мм; 3 – мм

Видно, что с увеличением параметра и, соответственно, с возрастанием площади колеблющейся кольцевой струйной пластинки, частота основной гармоники генерируемого сигнала для всех расчетных кривых монотонно уменьшается. При этом между теоретическими и экспериментальными данными для значений ширины кольцевой пластинки мм наблюдается хорошая корреляция. Сравнение теории с экспериментом (рис. 2) позволяет предложить критерий применимости разработанной модели для расчета частотных характеристик модифицированного жидкоструйного излучателя:

. (9)

В заключение отметим, что в результате решения задачи собственных колебаний кольцевой струйной пластинки получена аналитическая зависимость частоты основного тона акустического сигнала жидкоструйного преобразователя от геометрических параметров струи и свойств рабочей жидкости. При выполнении условия (9) излучатель генерирует акустический сигнал максимальной интенсивности [2], а ошибка расчета частоты основной гармоники по формуле (8) по сравнению с экспериментальными данными не превышает 5 %.

Литература:

1. Сухарьков О.В. Гидроакустическая излучающая рупорная антенна на основе жидкоструйного преобразователя / О.В. Сухарьков // Акустичний вісник. – 2011. – 14, № 1. – С. 56 – 63.

2. Сухарьков О.В. Энергетические характеристики затопленной кольцевой струйной пластинки при наличии развитой кавитации / О.В. Сухарьков // Акустичний вісник. – 2010. – 13, № 2. – С. 45 – 52.

3. Перцев А.К. Динамика оболочек и пластин / А.К. Перцев, Э.Г. Платонов. – Л.: “Судостроение”, 1987. – 400 с.

4. Сухарьков О.В. Модель жидкоструйного излучателя с круговым щелевым соплом в виде соосных дисков / О.В. Сухарьков // Наукові праці ОНАЗ ім. О.С. Попова. – 2011. – №2. – С. 107 – 113.

5. Корнфельд М. Упругость и прочность жидкостей / М. Корнфельд. – М.: ГТТИ, 1951. – 200 с.

6. Коренев Б.Г. Введение в теорию бесселевых функций / Б.Г. Коренев. – М.: Наука, 1971. – 288 с.

7. Янке Е. Специальные функции (Формулы, графики, таблицы) / Е. Янке, Ф. Эмде, Ф. Лёш. – М.: Наука, 1964. – 344 с.