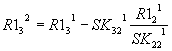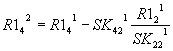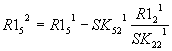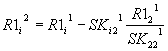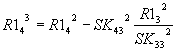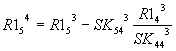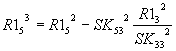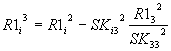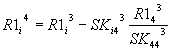Современные
информационные технологии/Вычислительная техника и программирование
Мясищев А.А.
Хмельницкий национальный
университет, Украина
Решение систем линейных уравнений на
двуядерных процессорах с использованием технологии OpenMP
При решении ряда прикладных
задач, описываемых дифференциальными уравнениями в частных производных,
возникает необходимость в решении систем линейных уравнений. В частности при
решении задач теории упругости, пластичности которые сводятся к решению систем
дифференциальных уравнений в напряжениях и скоростях, используется метод
конечных элементов. В свою очередь данный метод сводится к построению матриц
жесткости и решению систем линейных уравнений, содержащей тысячи и даже десятки
тысяч неизвестных. При решении пластических задач решение системы уравнений
приходится выполнять сотни и тысячи раз для выявления конечной конфигурации
деформируемого материала. Решение этих задач требует вычислительных систем
высокой производительности. В настоящее время широкое распространение получили
компьютеры с многоядерными процессорами. Например, двуядерные и
четырехядерные процессоры фирмы Intel и AMD.
Причем прогрессирование технологии производства процессоров в настоящее время
идет по пути увеличения числа ядер. И как отмечают производители, обычный
персональный компьютер с одним из таких процессоров превращается в параллельную
вычислительную систему с общей памятью (SMP-система). Проблема заключается в
том, чтобы распараллелить, например задачу решения систем линейных уравнений
так, чтобы получить максимальную загрузку многоядерного процессора и выигрыш в
производительности примерно соответствующий числу ядер. В качестве примера
рассмотрим решение системы линейных уравнений с использованием технологии OpenMP
и компилятора Фортран под управлением операционной системы ASP
Linx 11.2 на персональных компьютерах с двуядерными процессорами
Pentium E2160 и Athlon
64x2 4000+ .
Идея технологии OpenMP состоит в следующем. За
основу берется последовательная программа, а для создания ее параллельной
версии предоставляется набор директив.
Стандарт OpenMP разработан для языков Фортран, С и С++. Весь текст программы
разбивается на последовательные и параллельные области. В начальный момент
времени порождается нить-мастер или "основная" нить, которая начинает
выполнение программы со стартовой точки. При входе в параллельную область
порождаются дополнительные нити. После порождения каждая нить получает свой
уникальный номер, причем нить-мастер всегда имеет номер 0. Все нити исполняют
один и тот же код, соответствующий параллельной области. При выходе из
параллельной области основная нить дожидается завершения остальных нитей, и
дальнейшее выполнение программы продолжает только она. В параллельной области
все переменные программы разделяются на два класса: общие (SHARED) и локальные
(PRIVATE). Общая переменная всегда существует лишь в одном экземпляре для всей
программы и доступна всем нитям под одним и тем же именем. Объявление локальной
переменной вызывает порождение своего экземпляра данной переменной для каждой нити.
Изменение нитью значения своей локальной переменной не влияет на изменение
значения этой же локальной переменной в других нитях.
Все директивы OpenMP представлены в
программе в виде комментариев и начинаются, согласно синтаксису Фортран,
на один из трех символов: !, C
или *.
Для определения параллельных областей
программы используется пара директив
!$OMP PARALLEL
< параллельный код программы >
!$OMP END PARALLEL
Для выполнения кода, расположенного между
данными директивами, дополнительно порождается OMP_NUM_THREADS()-1 нитей.
Процесс, выполнивший данную директиву (нить-мастер), всегда получает номер 0.
Все нити исполняют код, заключенный между данными директивами. После END
PARALLEL автоматически происходит неявная синхронизация всех нитей, и как только
все нити доходят до этой точки, нить-мастер продолжает выполнение последующей
части программы, а остальные нити уничтожаются.
Все
порожденные нити исполняют один и тот же код. Для распределения работы между
ними часто используется директива DO. Иными словами если в
последовательной программе встретился оператор цикла DO то, используя директивы
!$OMP
DO
<do цикл>
!$OMP END DO
его можно распараллелить в параллельной
части программы.
Рассмотрим далее
последовательность решения системы линейных уравнений и программу на Фортране,
которая позволит рассчитать задачу последовательно на одном ядре процессора и
параллельно на двух ядрах.
Рассмотрим приведенную
ниже систему 5-и линейных уравнений,
которая записана в матричной форме:
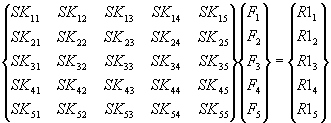(1)
Одним из наиболее эффективных методов
решения системы уравнений является метод исключения Гаусса. Матрица SK
системы уравнений преобразуется к треугольному виду (прямой ход) а затем
решение получается последовательным определением неизвестных, начиная с самого последнего уравнения
(обратный ход).
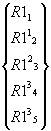
Рассмотрим прямой ход. В
этом случае матрица SK последовательно преобразуется к
треугольному виду за np-1 исключений. Здесь np –
число уравнений. Во время 1-го исключения из первого уравнения определяется
неизвестная 
. Затем она подставляется в оставшиеся 4-е уравнения и
исключается оттуда. Во время 2-го исключения из 2-го уравнения определяется
переменная 
и подставляется в
уравнения 3, 4 и 5 исключаясь из них. Далее поступают аналогично, пока в
последнем уравнении не останется только одна переменная 
. Во время таких исключений изменяются коэффициенты матриц SK
и R1
кроме первой строки.
1-е исключение:
=
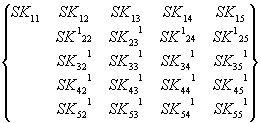
2-е исключение:
=
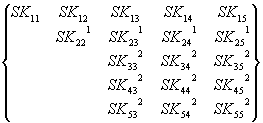
3-е исключение:
=
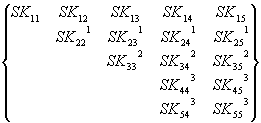
4-е исключение:
=
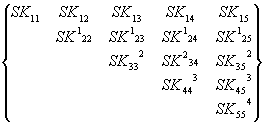
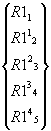(2)
Рассмотрим соотношения для определения
коэффициентов матрицы.
1-е исключение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Или в общем виде:
, i, j
> 1
2-е исключение:
|
|
|
|
|
|
|
|
|
|
|
|
Или в общем виде:
, i, j
> 2
3-е исключение:
|
|
|
|
|
|
Или в общем виде:
, i, j
> 3
4-е исключение:
Или в общем виде:
, i, j
> 5
После анализа
представленных выше зависимостей для n-го исключения можно
записать для членов матрицы SK общее соотношение вида:
, i, j
> n
Аналогично получается для вектора-столбца
R1.
|
1-е исключение: |
2-е исключение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий вид: |
Общий вид: |
|
3-е исключение: |
4-е исключение: |
|
|
|
|
|
|
|
Общий вид: |
Общий
вид:
|
После анализа представленных выше
зависимостей для n-го исключения можно записать для членов
вектора-столбца R1 общее соотношение вида:
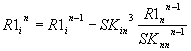, i>n
Рассмотрим
обратный ход. Из последнего уравнения соотношения (2) можно записать:
.
Подставляя значение 
в 4-е уравнение (2)
получим:
.
Аналогично можно получить и для 
, 
, 
:
;
;
;
Общее соотношение для неизвестной 
можно записать в виде
, 1 <= i < n
При i
= n
Анализ соотношений
показывает, что наибольшая вычислительная трудоемкость возникает при
преобразовании прямоугольной матрицы к
треугольному виду. Поэтому целесообразно вводить параллельные участки в этой
части вычислений. Ниже представлена программа на Фортране, составленная на
основе обобщенных зависимостей. В качестве компилятора использовался gfortran ver. 4.2.4 (gcc ver.4.2.4) под управлением ASP
Linux 11.2, который поддерживает технологию OpenMP.
program sys_line
parameter (np=5000)
real*8 sk(np,np), r1(np),f(np),sum,time1,time2
integer tickstart, tickstop, tickrate
integer ne,jj,i,j,nl
c Задание величин коэффициентов матриц
do 1 ii=1,np
do 1 jj=1,np
sk(ii,jj)=(ii+jj)/0.89d0
if(ii.eq.jj-1) then
sk(ii,jj)=10.0d0
end if
if(ii.eq.jj+1) then
sk(ii,jj)=2.0d0
end if
1 continue
do 2 ii=1,np
2 r1(ii)=(ii*21.d0+101.d0)/1.3d0
do 3 ii=1,np
3 f(ii)=0.0d0
c
c Прямой ход (выполняется параллельно)
c
call system_clock (tickstart, tickrate)
do nl=1,np-1
c Исключение с номером nl
!$OMP
PARALLEL shared(sk,r1),private(i,j)
!$OMP
DO
do i=nl+1,np
do j=nl+1,np
sk(i,j)=sk(i,j)-sk(i,nl)*sk(nl,j)/sk(nl,nl)
end do
r1(i)=r1(i)-sk(i,nl)*r1(nl)/sk(nl,nl)
sk(i,nl)=0.d0
end do
!OMP
END DO
!$OMP
end parallel
c Конец исключения
end do
c
c Конец прямого
хода
c
call system_clock (tickstop)
time1 = float (tickstop - tickstart) /
float(tickrate)
c
c Обратный ход (выполняется последовательно)
c
call system_clock (tickstart, tickrate)
f(np)=r1(np)/sk(np,np)
do k=1, np-1
i=np-k
sum=0.d0
ne=np-k+1
do j=np,ne,-1
sum=sum+sk(i,j)*f(j)
end do
f(i)=(r1(i)-sum)/sk(i,i)
end do
c
c Конец обратного хода
c
call system_clock (tickstop)
time2 = float (tickstop - tickstart) /
float(tickrate)
time=time1+time2
print *, 'Результат счета'
print 11, time1,time2
11 format('Time1=',f10.4,' Time2=',f10.4)
print *,'Общее время
счета=',time
print 10 ,f(np-4),f(np-3),f(np-2),f(np-1),f(np)
10
format(1x,5f12.7)
end
Компиляция и запуск программы проводился
последовательностью команд:
export LD_LIBRARY_PATH=/usr/local/lib
gfortran
–O2 -fopenmp -o sys_line
sys_line.f
./sys_line
при параллельном исполнении программы
и
gfortran
–O2 -o sys_line sys_line.f
./sys_line
при последовательном. Параметр –O2
сообщает компилятору о необходимости оптимизации кода.
Расчет проводился на
двух компьютерах с процессорами Pentium E2160
и Athlon 64x2 4000+ для разного
числа линейных уравнений и для параллельного и последовательного исполнения
программы. Результат экспериментального счета для компьютера с процессором Athlon
64x2 4000+ представлен в таблице 1, для компьютера с
процессором Pentium E2160 – в таблице 2.
Таблица 1.
|
Число уравнений в
системе |
Время счета одним
ядром, с. |
Время счета двумя
ядрами, с. |
Ускорение |
|
400 |
0.28 |
0.23 |
1.22 |
|
500 |
0.56 |
0.30 |
1.87 |
|
1000 |
9.56 |
5.52 |
1.73 |
|
2000 |
112.48 |
62.02 |
1.81 |
|
3000 |
452.26 |
245.51 |
1.84 |
|
4000 |
2049.03 |
1691.93 |
1.21 |
|
5000 |
6145.15 |
3779.92 |
1.63 |
Таблица 2.
|
Число уравнений в
системе |
Время счета одним
ядром, с. |
Время счета двумя
ядрами, с. |
Ускорение |
|
400 |
0.72 |
0.37 |
1.95 |
|
500 |
1.38 |
0.76 |
1.82 |
|
1000 |
8.84 |
4.72 |
1.87 |
|
2000 |
72.98 |
42.19 |
1.73 |
|
3000 |
249.03 |
156.91 |
1.59 |
|
4000 |
1125.48 |
1054.40 |
1.07 |
|
5000 |
2275.32 |
1819.37 |
1.25 |
При работе программы выводилось время
прямого хода (time1) и обратного (time2). Ни в одном случае
расчета отношение времен прямого и обратного хода не было меньше значения 3000
для последовательного варианта расчета (на одном ядре). Поэтому в программе
обратный ход не распараллеливался. Из таблиц видно, что для процессора Athlon
64x2 4000+ распараллеливание целесообразно, если число
уравнений системы 500<np<3000 и np>5000. А для Pentium
E2160 np<
2000. В этом случае эффект от распараллеливания будет наилучшим. Также видно,
что при np<1000 уравнений Athlon выигрывает в
производительности, но при большем числе начинает сильно проигрывать. Поэтому Athlon
целесообразно использовать для решения малых систем уравнений, а E2160 для больших.
Литература.
1. Воеводин В.В., Воеводин Вл.В.
Параллельные вычисления. –СПб: БХВ – Петербург, 2004.-608 с.: ил.
2. Гергель В.П. Теория и практика
параллельных вычислений. http://www.intuit.ru/department/calculate/paralltp/ - 2007.