Математика / 4. Прикладная математика

К.ф.-м.н. Айпанов Ш.А., Сатов А.Е.

КазНУ им. аль-Фараби, РСФМСШИ им. О.Жаутыкова,

г. Алматы, Казахстан

ДИАГРАММА АЙНСА – СТРЕТТА И ОРБИТАЛЬНАЯ

УСТОЙЧИВОСТЬ КОСМИЧЕСКОГО АППАРАТА

Введение. Работа посвящена исследованию устойчивости движения космического аппарата (КА), вращающегося вокруг Земли по круговой орбите. Рассмотрены уравнения возмущенного движения КА при учете силы притяжения Луны. Показано, что в первом приближении эти уравнения соответствуют уравнениям движения математического маятника с вибрирующей точкой подвеса, который относится к хорошо исследованному классу механических систем. Тем самым становится возможным использование известных математических методов исследования устойчивости колебательных систем [1].

Для исследования устойчивости решений систем дифференциальных уравнений с периодическими коэффициентами можно использовать метод Ляпунова, метод усреднения [1, 2] и др. методы. Устойчивость маятника с вибрирующей точкой подвеса, исследована, например, в [2] с использованием метода усреднения и показано, что при некоторых частотах вибрации нижнее устойчивое состояние маятника может стать неустойчивым из-за резонансных явлений, и наоборот, верхнее неустойчивое состояние маятника можно сделать устойчивым с помощью высокочастотной вибрации.

Теория резонансных явлений в колебательных системах находит широкое применение в исследовании динамики небесных тел. Например, наличие узких «щелей» между кольцами Сатурна можно объяснить резонансными явлениями (как следствие влияния Сатурна и его многочисленных спутников), которые приводят к появлению орбит, движение по которым является неустойчивым. Аналогично, орбиты планет Солнечной системы также могут «квантоваться». Тем самым, приходим к идее о возможности квантования орбит космических объектов: существуют орбиты, движение по которым является устойчивым. Это напоминает планетарную модель атома Бора – Резерфорда, в которой электроны движутся вокруг ядра по некоторым «разрешенным» орбитам, соответствующим определенным квантовым уровням.

Целью данной работы является исследование устойчивости орбит КА с использованием упрощенной модели задачи трех тел «Земля – КА –Луна».

1. Устойчивость математического маятника с вибрирующей точкой подвеса. Рассмотрим уравнения движения математического маятника с вибрирующей точкой подвеса, а также приведем известные результаты об условиях возникновения параметрического резонанса (когда нижнее положение равновесия маятника становится неустойчивым) и об условиях, когда верхнее положение равновесия можно сделать устойчивым за счет вибрации (при этом маятник будет совершать устойчивые колебания в перевернутом состоянии). Эти результаты в дальнейшем будут использованы для исследования устойчивости орбит КА.

Пусть материальная точка с массой m закреплена на конце стержня длины l, который может вращаться вокруг горизонтальной оси O. Обозначим через угол отклонения маятника от вертикали. Очевидно, что такой маятник имеет два положения равновесия: нижнее устойчивое и верхнее неустойчивое. Исследуем влияние вертикальных колебаний точки подвеса O на характер равновесия маятника. Будем считать, что точка подвеса вибрирует по гармоническому закону .

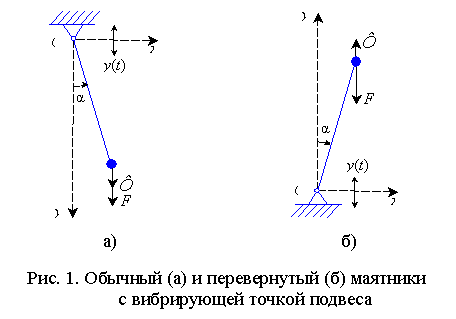
а) Рассмотрим колебания маятника около нижнего положения равновесия (рис. 1а). Перейдем в неинерциальную систему координат, связанную с точкой подвеса O. В этой системе координат на маятник действуют сила тяжести и переносная сила инерции . По второму закону Ньютона можно написать уравнение движения:

, (1)

где . Для малых значений угла отклонения уравнение (1) принимает вид

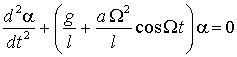. (2)

Вводя обозначение , уравнение (2) можно привести к виду

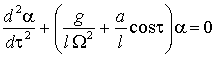. (3)

Таким образом, имеем уравнение вида

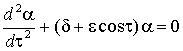, (4)

которое называется уравнением Матье. Отметим, что для рассматриваемой задачи параметр является положительным: (здесь через 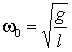обозначена частота свободных колебаний маятника при отсутствии вибрации точки подвеса).

Известно, что вблизи значений наступает так называемый параметрический резонанс [2] и положение равновесия становится неустойчивым. Последовательно присваивая параметру значения , 1, , 4, , 9, ... , получаемые соответственно при , имеем, что параметрический резонанс наступает вблизи частот

, , , , , , ... . (5)

б) Для вывода уравнения движения маятника вблизи верхнего положения равновесия (рис. 1б) достаточно в уравнении (3) заменить g на :

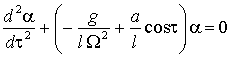, (6)

т.е. перевернутый маятник с вибрирующей точкой подвеса также описывается уравнением Матье (4), где параметр является отрицательным: .

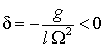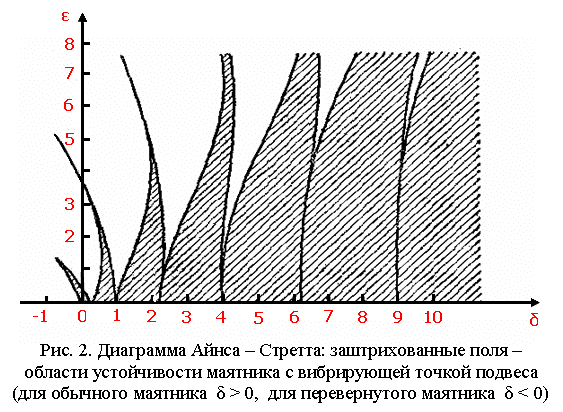
Устойчивость решения уравнения (4) достаточно хорошо исследована (см. например, [2]). Область устойчивости уравнения Матье на плоскости параметров представлена на рис. 2 в виде диаграммы Айнса – Стретта. Диаграмма дана только для значений , а для значений она получается зеркальным отображением относительно оси .

Как видно из диаграммы, при малых значениях (т.е. ) нижнее положение равновесия маятника становится неустойчивым вблизи значений , , , , , , ... из-за параметрического резонанса.

Из диаграммы также следует, что в принципе возможно обеспечение устойчивости при (т.е. можно стабилизировать движение перевернутого маятника с помощью вибрации). Для значений << 1 условия устойчивости перевернутого маятника записываются в виде [2]

. (7)

Будем считать, что амплитуда колебаний точки подвеса мала по сравнению с длиной маятника . Тогда и из (7) можно получить соотношения

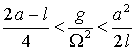. (8)

При первое неравенство выполняется всегда, а из второго неравенства имеем

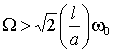, (9)

т.е. для стабилизации движения перевернутого маятника частота вибрации точки подвеса должна быть достаточно большой по сравнению с частотой свободных колебаний маятника .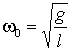

Основной вывод, который можно сделать из вышесказанного, заключается в том, при изменении частоты вибрации точки подвеса происходит чередование свойств устойчивости и неустойчивости (маятник становится неустойчивым вблизи частот (5) из-за параметрического резонанса). Данный результат особо важен для обоснования квантования орбит космических объектов, т.е. факта существования устойчивых орбит, между которыми имеются «щели», соответствующие неустойчивым орбитам.

Следует особо отметить также, что условия параметрического резонанса (5) не зависят от – амплитуды внешнего воздействия , а зависят только от его частоты . Это говорит о том, при исследовании устойчивости космических объектов слабые взаимодействия (например, сила притяжения Луны для КА) могут играть существенную роль, поскольку здесь имеет значение именно частота, а не амплитуда.

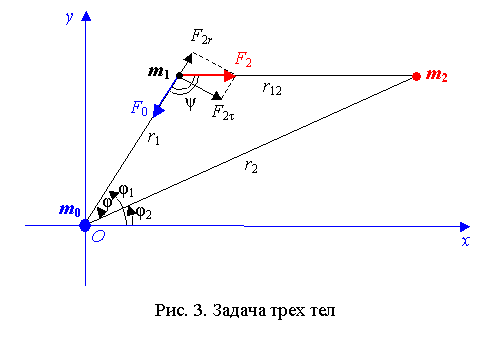
2. Космический аппарат как маятник с вибрирующей точкой подвеса. Перейдем теперь к выводу уравнений движения КА. Конечно, траектория движения КА, рассчитанная с учетом влияния Земли, Луны и Солнца, представляет собой довольно сложную кривую в пространстве. Но мы рассмотрим здесь упрощенную математическую модель задачи трех тел «Земля – КА – Луна» в «плоском» варианте (рис. 3): предположим, что орбита КА расположена в плоскости орбиты Луны. Обозначим через и массы Земли, КА и Луны соответственно (, ). Будем считать, что Луна движется по круговой орбите радиуса относительно центра Земли, а невозмущенная траектория КА является окружностью радиуса относительно центра Земли, где – радиус Земли, – высота орбиты КА над поверхностью Земли. Вследствие влияния Луны траектория КА будет отклоняться от невозмущенной круговой орбиты. Влияние Солнца на траекторию КА мы здесь не учитываем.

Для дальнейших расчетов нам понадобятся и – угловые скорости вращения КА и Луны относительно центра Земли. Угловая скорость КА равна

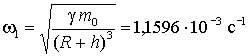, (10)

что соответствует периоду вращения 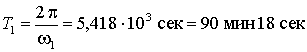; а угловая скорость вращения Луны равна

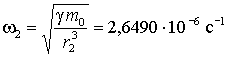, (11)

где 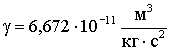– гравитационная постоянная.

Векторы скоростей тел и обозначим через и соответственно. Разложим вектор на составляющие: , где и – радиальная и тангенциальная составляющие скорости . Аналогично, . Поскольку радиальная и тангенциальная компоненты скорости перпендикулярны между собой, имеют место следующие соотношения:

, ,

где , , , .

Кинетическая энергия равна:

.

Потенциальная энергия вычисляется следующим образом:

.

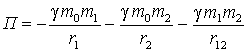Для определения расстояния рассмотрим треугольник с вершинами в (рис. 3). Обозначая угол при вершине через , можно вычислить расстояние между и :

.

Для упрощения расчетов будем предполагать, что , где и – угловые скорости КА и Луны определяются по формулам (10) и (11) соответственно; .

Далее найдем частные производные функции по переменным :

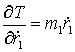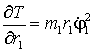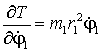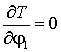, , , (12)

и частные производные функции по переменным и :

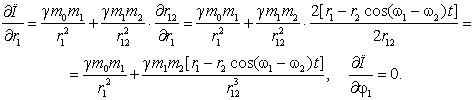(13)

Для вывода дифференциальных уравнений, описывающих движение тела относительно переменных и , воспользуемся уравнениями Лагранжа второго рода [2]:

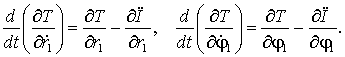(14)

Подставляя в (14) найденные ранее выражения для частных производных из (12), (13), получим

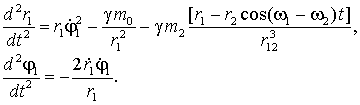(15)

где 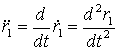, 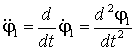. В качестве невозмущенного движения выберем частное решение системы дифференциальных уравнений (15) при некоторых начальных условиях , , , . Обозначим отклонения от невозмущенного движения через , , , . Разлагая в ряд Тейлора правые части уравнений (15) относительно невозмущенного движения и ограничиваясь только линейными членами разложения, получим дифференциальные уравнения первого приближения:

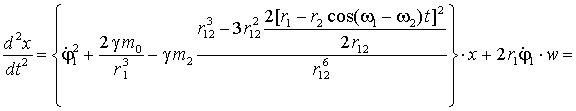
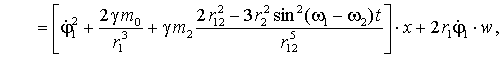
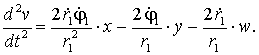
Расстояние между и изменяется в пределах , т.е. . Для упрощения расчетов примем , , , . Тогда с учетом формул (10), (11) получим

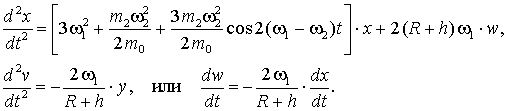(16)

Из второго уравнения системы (16) следует, что , причем константа , поскольку на невозмущенной траектории имеем , . Таким образом, первое уравнение системы (16) можно записать в виде

,

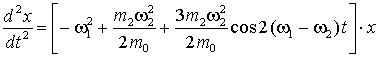или

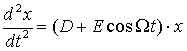, (17)

где 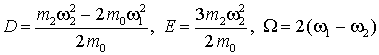. Разделим обе части уравнения (17) на :

.

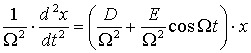Далее, вводя новую переменную , получим дифференциальное уравнение

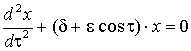, (18)

где

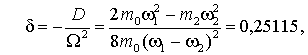
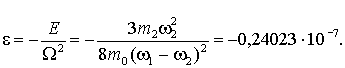(19)

Как видим, полученное соотношение (18) представляет собой уравнение Матье (4), причем , что соответствует уравнению движения обычного (не перевернутого) маятника с вибрирующей точкой подвеса.

Таким образом, показано, что уравнения движения КА на околоземной орбите, составленные с учетом влияния Луны, в первом приближении соответствуют уравнениям движения маятника с вибрирующей точкой подвеса и для исследования устойчивости КА можно воспользоваться диаграммой Айнса – Стретта (рис. 2). При вблизи точки параметрический резонанс наступает при выполнении неравенств [2]

. (20)

Для вычисленных нами значений и (19) условия (20) не выполняются, следовательно, в рассматриваемой задаче орбита КА является устойчивой.

Выводы. Работа посвящена исследованию устойчивости орбит КА при учете влияния Луны. Показано, что в первом приближении уравнения движения КА соответствуют уравнениям движения маятника с вибрирующей точкой подвеса, для которого известны такие интересные свойства как чередование свойств устойчивости и неустойчивости при изменении частоты вибрации, устойчивость перевернутого маятника при некоторых частотах вибрации. Математический маятник относится к классу достаточно хорошо изученных колебательных систем. Основной результат работы заключается в том, что показана возможность использования ранее известных результатов об устойчивости движения маятника для исследования свойств орбит КА.

О возможности чередования устойчивых и неустойчивых околопланетных орбит наглядно свидетельствует структура колец Сатурна. Это наталкивает на мысль о том, что орбиты КА, вращающихся вокруг Земли, в принципе тоже могут «квантоваться». Аналогичным образом может быть исследована устойчивость движения планет Солнечной системы при учете влияния других планет. Самой первой гипотезой о возможности квантования орбит планет Солнечной системы было правило Тициуса – Боде [3]. Существуют несколько попыток его обоснования, в частности, принадлежащие О.Ю. Шмидту и В.Г. Фесенкову. Однако в настоящее время данное правило относят к области нумерологии, считая его «игрой чисел», случайным совпадением, а не научным законом.

Для космического аппарата силы притяжения спутников планеты могут быть в миллионы раз меньше силы притяжения самой планеты и на первый взгляд может показаться, что можно в принципе пренебречь этими слабыми взаимодействиями. Но как отмечено в работе, для возникновения резонансных явлений существенную роль играет не амплитуда, а частота внешнего возмущения. Так что «слабые» взаимодействия могут иметь «сильные» последствия и привести к неустойчивости орбит КА.

Рассмотренная в работе математическая модель задачи трех тел «Земля – КА – Луна» дает упрощенное описание динамики КА в первом приближении и позволяет представить лишь общую картину влияния Луны на устойчивость орбит КА. Более сложной является математическая модель, где орбиты КА и Луны могут лежать в разных плоскостях, кроме того, надо учесть вращение Земли и Луны относительно их центра масс и движение этого центра масс относительно Солнца и т.д. Таким образом, в дальнейшем требуется использование более точных математических моделей и более сложных математических методов.

Литература

1. Боголюбов Н.Н., Митропольский Ю.А.. Асимптотические методы в теории нелинейных колебаний. – М: ГИФМЛ, 1963. – 412 с.

2. Меркин Д.Р. Введение в теорию устойчивости движения. – СПб: Лань, 2003. – 304 с.

3. Маженов Н. Маленькая книжка о большой Вселенной. – Алматы, 2000. – 112 с.