Математика / 4.Прикладная математика

К.ф.-м.н., доцент Быкова И.Ю.

Восточно-Казахстанский государственный технический университет, Казахстан

Агрегирование индивидуальных предпочтений

в условиях неопределенности

Большинство действий предпринимаемых лицами, принимающими решения, может быть объяснено лишь как результат проявления различных взаимодействующих сил и действий, предпринимаемых многими другими лицами, руководствующимися разнообразными мотивами. С другой стороны, поскольку процесс принятия решения синтезируется в сознании совершенно конкретных людей, а, значит, каждый групповой выбор решения определяется личным решением индивидуумов.

Для выбора лучшей альтернативы в условиях неопределённости нам потребуется функция полезности лица, принимаемого решение, обозначим её через u для последствий x. Обозначим через U1,U2,..,UN критерии, по которым выражается с помощью функций полезности индивидов u1, u2,..uN. Когда рассматривается “чистая” модель принятия решения в условиях неопределённости, то ставится задача найти подходящий вид функции uD, такой, что u(x)= uD [u1(x), u2(x), .. , uN(x)], где u, uD - функции полезности лица, принимающего решение.

Эта модель основана на ряде допущений. Харшаньи Дж.К. сформулировал совокупность необходимых и достаточных условий для того, чтобы групповая функция полезности могла быть выражена в виде взвешенной суммы функций полезности от u1 до uN, т.е. .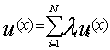

Принципиальную роль в рассуждениях Харшаньи играет следующее допущение.

Допущение Харшаньи. Если две альтернативы, определяемые распределениями вероятностей реализации последствий x, одинаковы по их предпочтительности для каждого индивида, то они одинаковы по предпочтительности и для всей группы.

Сформулируем ещё несколько допущений.

Допущение об аддитивной независимости. Множество критериев U1,U2,..,UN аддитивно независимо.

Допущение о стратегической эквивалентности. Условная функция полезности лица, принимающего решение, ui* для критерия Ui, представляющего собой полезность для индивида i, стратегически эквивалентна функции полезности индивида i .

При N³ 2 допущение об аддитивной независимости и допущение о стратегической эквивалентности справедливы тогда и только тогда, когда , где ui, i=1,2,..,N - функция полезности индивида i со шкалой от 0 до 1, li - положительные шкалируемые коэффициенты и x - последствие.

Сравнение со стороны лица, принимающего решение, предпочтений индивидов необходимо для нахождения значений шкалируемых коэффициентов li.

Допущение о положительной связи предпочтений. Пусть некоторые альтернативы a и b будут для группы одинаковы по предпочтительности. Если a изменится и превратиться в альтернативу a* таким образом, что какой- либо индивид c предпочтёт альтернативу a* альтернативе a, в то время, как все остальные лица считают их равноценными, то тогда a* предпочитается альтернативе b всей группой.

Допущение о независимости по полезности. Каждый из критериев Uj, ji, j=1,2,..,N, не зависит по полезности от остальных критериев .

Согласно этому допущению функция полезности u(x) будет иметь следующий вид u(x)= uD(u1,..,ui,..,uN)= gi()+fi()ui*(ui), для всех i, где (u1,..,ui-1,ui+1,..,uN), все fi - положительны, а ui* - условная функция полезности лица, принимающего решение, для критерия Ui. При N³ 2 где шкалы для измерения u и ui выбраны так, чтобы значения этих функций лежали в диапазоне от 0 до 1, l - шкалирующие коэффициенты и 0<li<1 для всех i.

Допущение о всеобщем согласии. Если все члены группы имеют одну и ту же функцию полезности, тогда групповая функция полезности должна быть общей функцией полезности для всех членов.

Весь этот аппарат позволяет нам рассматривать агрегирование индивидуальных предпочтений как некоторую задачу нечеткого математического программирования. Об этом подробнее можно узнать из третьего параграфа данной главы. Выше изложенный аппарат позволит нам строить некоторую групповую функцию полезности, и, агрегируя каждые индивидуальные предпочтения, строить групповые предпочтения.

При исследовании процесса с целью принятия рационального решения лучше начать с множества всех допустимых решений или альтернатив. В зависимости от имеющейся информации это множество удается описать с той или иной степенью чёткости. Пусть X - некоторое универсальное множество альтернатив (например, множество недоминируемых альтернатив по Парето) и mC(x) - нечёткое описание его подмножества допустимых альтернатив. Значения функции mC описывают степени допустимости соответствующих альтернатив в данной задаче. Если кроме этой функции нет другой информации об исследуемой реальной ситуации, рациональным считается выбор любой альтернативы из множества

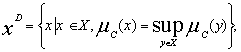
т.е. любой альтернативы, имеющей максимальную степень допустимости, поскольку нет оснований предпочесть какую-либо из этих альтернатив остальным.

Один из способов выявления отношения предпочтения при построении математической модели - консультации с лицом, принимающим решение, или экспертами. При этом имеется в виду, что лицо, принимающее решение, или эксперты обладают знаниями или представлениями об исследуемом объекте, которые не были формализованы в модели в силу чрезмерной сложности такой формализации или по другим причинам.

Допустим, что с помощью лица, принимающего решение, или экспертов выявлено чёткое отношение нестрогого предпочтения R в множестве допустимых альтернатив X. Это значит, что относительно любой пары альтернатив x,yÎ X высказано одно из следующих утверждений.

Утверждение 1. “x не хуже y”, т.е. x³ y или (x,y)Î R.

Утверждение 2. “y не хуже x”, т.е. у³ х или (x,y)Î R.

Утверждение 3.”x и y не сравнимы между собой “, т.е. (x,y)ÏR и (x,y)Ï R.

Информация в такой форме позволяют сузить класс рациональных выборов, включив в него лишь те, которые не доминируются ни одной альтернативой множества X .

Для того чтобы пояснить, какие альтернативы считаются недоминируемыми, выделим соответствующие отношению предпочтения R отношение строгого предпочтения RS и отношение безразличия RI .

Будем говорить, что альтернатива x строго лучше альтернативы y, если одновременно x³ y и yx, т.е. (x,y)Î R и (y,x)Ï R. Совокупность таких пар (x,y) назовём отношением строгого предпочтения RS на множестве X.

Пара (x,y)Î RI тогда и только тогда, когда либо не выполнено предпочтение x³ y, ни предпочтение y³ x, либо оба предпочтения выполнены одновременно. Иными словами, (x,y)Î RI, когда имеющаяся информация в форме отношения предпочтения недостаточна для того, чтобы сделать выбор между альтернативами x и y.

Если (x,y)Î RS, то будем говорить, что альтернатива х доминирует альтернативу у (ху). Альтернативу xÎX назовём недоминируемой в множестве (X,R), если (y,x) Ï RS для любой альтернативы yÎ X. Иными словами, если x -недоминируемая альтернатива, то в множестве X нет ни одной альтернативы, которая бы доминировала x. Недоминируемые альтернативы являются в определённом смысле неулучшаемыми на множестве (X,R), и их выбор в задаче принятия решений по праву считается рациональным.

Таким образом, информация в форме отношения предпочтения R позволяет сузить класс рациональных выборов в X до множества недоминируемых альтернатив вида

Чем больше имеется информации о реальной ситуации, тем уже отношение безразличия, уже множество Xн.д. и, следовательно, меньше неопределенность в рациональном выборе альтернатив.

Более гибким способом формализации имеющихся у экспертов знаний о реальной ситуации представляется такой, при котором они имеют возможность описывать степень своей убеждённости в предпочтениях между альтернативами числами из интервала [0,1]. В результате с помощью экспертов выявляется нечёткое отношение предпочтения в множестве альтернатив, в котором каждой паре (x,y) соответствует число, описывающее степень выполнения предпочтения x³ y . Этот способ описания отношения позволяет в более полной мере ввести в математическую модель знания и представления экспертов и тем самым сделать модель в определенном смысле более адекватной реальности.

Пусть задано множество альтернатив x и каждая альтернатива характеризуется несколькими признаками с номерами j=1,...,m. Информация о попарном сравнении альтернатив по каждому из признаков j представлена в форме отношения предпочтений Rj. Таким образом, имеется m отношений предпочтения Rj на множестве X . Пусть отношения Rj описываются заданными функциями полезности fj : X®R1, где R1 — числовая ось. Значение функции fj(x) можно понимать как числовую оценку альтернативы x по признаку j. Альтернатива с большей оценкой fj(x) полагается более предпочтительной по признаку j. Задача заключается в том, чтобы по имеющейся информации сделать рациональный выбор альтернатив на множестве (X,R1,...,Rm), т.е. выбрать альтернативу, имеющую по возможности большие оценки по всем признакам.

Рациональным в этом случае считается выбор альтернативы x0ÎX, обладающей свойствами fj(y)³ fj(x0), j=1,..,m Þfj(y)= fj(x0), j=1,..,m. Тогда, каждая из функций полезности fj описывает обычное отношение предпочтения на X следующего вида

Rj={(x,y)| x,yÎ X, fj(x)³ fj(y)}.

Множество - множество всех недоминируемых альтернатив в множестве (x,Q1), которое совпадает с набором недоминируемых альтернатив для набора функций fj, j=1,...,m.

Представим теперь пересечение отношений Rj в несколько иной форме. Пусть — функция принадлежности отношения Rj. Тогда Q1 соответствует функция принадлежности mQ1(x,y)=min{m1(x,y),...,mm(x,y)}, аналогичная свёртке критериев fj вида , применяемой в многокритериальных задачах. Числа lj в этой свёртке играют роль коэффициентов относительной важности рассматриваемых функций.

В результате свёртки исходных отношений Rj с коэффициентами lj такими, что , получаем функцию принадлежности вида

mQ1(x,y)=min{l1m1(x,y),.., lmmm(x,y)},

т.е. функцию принадлежности нечёткого отношения предпочтения.

Введём теперь свёртку другого вида . Такая свёртка по набору функций принадлежности позволяет получить дополнительную информацию об относительной степени недоминируемости альтернатив и тем самым сузить класс рациональных выборов до множества

,

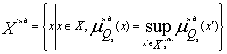где mQ2н.д.(x)=1-sup[mQ1(y,x)-mQ2(x,y)] - нечёткое подмножество недоминируемых альтернатив на множестве (X, mQ2), X2н.д. -подмножество недоминируемых альтернатив на множестве (X, mQ2).

Рациональным будет выбор альтернативы, имеющей максимальную степень недоминируемости, т.е. имеющей наибольшее значение функции m н.д..

Пусть теперь задано множество альтернатив (или объектов) X и задано множество признаков (или экспертов) P. Каждой альтернативе xÎX в той или иной степени присущ каждый из признаков множества P. Для каждого фиксированного признака pÎ P известно нечёткое отношение предпочтения j на множестве альтернатив X или, иными словами, известна функция принадлежности j : X´X´P® [0,1], значение j(x1,x2,p) которой понимается как степень предпочтительности альтернативы x1 альтернативе x2 по признаку p. Если P - множество экспертов, то j(x1,x2,p) - отношение предпочтения на множестве альтернатив, предлагаемое экспертом p. Таким образом, функция j описывает семейство нечётких отношений предпочтения на множестве X по параметру p. Элементы множества P, различны по важности. Пусть m:P´P®[0,1] — заданное нечёткое отношение важности признаков (экспертов); величина m(p1,p2)понимается как степень, с которой признак p1 считается менее важным, чем признак p2.

Пусть j н.д.(x, p) - нечёткое подмножество недоминируемых альтернатив, соответствующее нечёткому отношению предпочтения j(x1,x2,p) при фиксированном pÎP, т.е. справедлива следующая запись

.

Если бы выбор осуществился лишь с учётом одного признака p, то рациональным следовало бы считать выбор альтернатив, достигающих по возможности большее значение функции принадлежности jн.д.(x, p) (степени недоминируемости) на множестве X. В данном же случае нужно осуществить выбор с учётом совокупности признаков, различающихся по важности.

При фиксированном x0ÎX функция j н.д.(x0, p) описывает нечёткое подмножество признаков, по которым альтернатива x0 является недоминируемой. Если для двух альтернатив x1, x2 нечёткое множество признаков j н.д.(x1, p) “не менее важно”, чем нечёткое множество признаков j н.д.(x2, p), то альтернативу x1 следует считать не менее предпочтительной чем, альтернатива x2 .

В данном случае нужно обобщить заданное нечёткое отношение m(p1,p2)на множестве признаков P на класс нечётких подмножеств множества P и считать полученное нечёткое отношение результирующим нечётким отношением предпочтения на множестве альтернатив X. Введем нечёткое отношение предпочтения на множестве X, индуцированное функцией j н.д.(x, p) и нечётким отношением m,

Это нечёткое отношение предпочтения можно рассматривать как результат «свёртки» семейства нечётких отношений j(x1,x2,p) в единое нечёткое отношение предпочтения с учётом информации об относительной важности признаков, заданной в форме нечёткого отношения.

Построением нечеткого отношения предпочтения h исходная задача выбора сведена к задаче выбора с единственным отношением предпочтения. Для её решения достаточно определить соответствующее отношение h, скорректированное нечёткое множество недоминируемых альтернатив и выбрать альтернативы, доставляющие максимум функции h н.д.(x).