Òåõíè÷åñêèå íàóêè/Ìåòàëëóðãèÿ

Zhiguts Yu.Yu., Talabirchuk V.Yu., Batryn I.I.

Uzhgorod National University, Ukraine

EXTENSION OF THE HILLERT METHOD UPON COMPUTING OF COMPONENT ACTIVITIES OF TRIPLE SYSTEMS ON TWO- AND THREE-PHASE REGIONS OF ISOTERMIC SECTIONS OF STATE DIAGRAMS

While using classic Hillert method [1] and its modifications [2] the most significant initial value in computation of activities a_i along the tie-line of two phase region of given isothermal section of three-component (angle h of system h-i-j) diagram of state is the activity a_iº along the same name tie-line of double system hi. But it provides for two-phase region being situated closely to diagram hi. And what if this not so? In such a case it is necessary to know the activity a_iº along the least of one tie-line of three component two-phase region α+β and then this tie-line is taken as the base one although it is inclined to the axis hi (ν_j=0) and the latter is removed from the region α+β.

The isothermal section is done in Skreinemakers coordinates because it allows applying in the computations a wary simple and sharp Hillert-Zhukov equation, in which the coordinates of tie-points or of figurative points of alloys are absent:

(1)

where a_iº – component activity along the basic (“zero”) tie-line at X_i=0 (binary system h³, when the region α+β is contiguous after this tie-line to binary diagram hi); – tangent of the angle of tie-line inclination of two-phase balance in the system under investigation hij.

This allows in its turn for the case to make computation a_i along the tie-line α_²β_² by equation:

(2)

where and – tangents of angles of tie-line α_Ιβ_² and α₀β₀; a_i^b – known value a_i along basic tie-line α₀β_0.

Computation for tie-line α_²²β_²² is being made in the sawed way using the equation:

(3)

where – inclination of tie-line α_²²β_²².

It is easy to make sure that the original Hillert equation [1] that contains tie-line coordinates (to say nothing of great approximations needed while it was being deduced [2]) isn’t used for such computation as while coming from tie-line α₀β₀ to tie-line α_Ιβ_Ι and then to tie-line α_ΙΙβ_ΙΙ these coordinates change greatly.

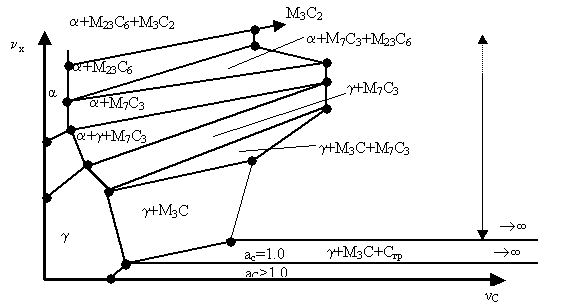In Fig. 1 as an example the applying of the method investigated is shown to isothermal section (in the region of supercritical temperatures) of systems Fe-C-X (where X – manganese, chromium or their analogs). In two-phase region g+C_gr (austenite+graphite) the activity of carbon is more than 1.0. In the tie-line triangle g+M₃C+C_gr (austenite+alloyed+graphite) the activity of carbon is constant after definition (a_C=1.0). These alloys aren’t able to graphitize above the given triangle a_C<1. The tie-line g+M₃C of the mentioned triangle serves as base tie-line α₀β₀ along its a_C=1.0.

Fig. 1. Schema isothermal section of state diagram of Fe-C-X, alloys in which under a_C>1,0 graphite is formed (under condition that graphite is been selected as a standard state of carbon) and carbide phases M₃C (cementite), M₇C₃, M₂₃C₆ and M₃C₂

Using of the computations according to equation of type (2) and (3) in the region g+M₃C (here the activity decreases monotonously to the value a_C<1,0) to the tie-line g+M₃C of the next tie-line triangle g+M₃C+M₇C₃ (activity a_C degreases because , and consequently, increase progressively). In the mentioned triangle carbon activity is constant and it allows us to use equations (2) and (3) for computations in tetragon g+M₇C₃, where the activity a_C continues to degrease with the increasing of the level of dopingness of alloys. The triangle α+γ+M₇C₃, in the inner part of which the carbon activity is constant allows to move the value a_C from the lower right tie-line of triangle to the upper tie-line and to continue computations by the equation of (2) and (3) type in the tetragon α+M₇C₃. Prolonging the above mentioned structure for the regions laying above the triangle α+M₂₃C₆+M₇C₃, the tetragon α+M₂₃C₆ and triangle α+M₂₃C₆+M₃C₂ we can lead the computations to the region of highchrome alloys but with large degree of approximation (because the Hillert method, in principal, is perfectly designed only for deluded systems).

Conclusions: 1. The Hillert method is also spread to tie-lines of two-phase regions of triangle simplexes of tree-component diagrams of state Må-C, when these regions are removed from those sides of the mentioned triangles which in two-component under investigation in the computations of its activity. 2. The original Hillert method proved to be unserviceable to solve this problem in contrast to modified method, which uses Screinemakers orthogonal system of coordinates. 3. The reason of this lies in the fact that the modified method doesn’t demand the definition and usage in the computations the coordinates of the corresponding tie-point.

References:

1. Hillert M. On isoactivity lines/ Acta metallurgica, Vol. 1 (1955), p. 34-37.

2. Zhukov A.A., Ramani A.S., Zhiguts Yu.Yu. Modifications of Hillert equation and their application in phase diagram computation. OPA. Amsterdam B.V. Metal Physics and Advanced Technologies. 1997. Vol.16. p. 821–839.