Отраслевое машиностроение-3
Корчак Н.Н.
Андреев А.А.
Подольский
государственный аграрно-технический университет
Динамические свойства
малоинерционных выравнивающих устройств
В настоящее время существуют и интенсивно
разрабатываются технологии, предназначенные
для тонкого выравнивания горизонтальных поверхностей сыпучих материалов.
Потребность в таких технологиях возникает в целом ряде отраслей промышленности,
а именно: в почвообрабатывающей, пищевой, фармакологической и т.д. Механические
устройства для реализации этих технологий могут быть различными, но самые
простые из них неизбежно имеют следующее свойство: чем более тонкое
выравнивание поверхности, тем менее массивными становятся исполнительные
рабочие органы. Иными словами, инерционность рабочих органов уменьшается до
такой степени, когда уже нельзя пренебрегать целым рядом динамических свойств,
несущественных для сравнительно массивных рабочих органов.
Совершенно очевидным является неизбежное
усложнение математического аппарата, используемого при проведении динамических
расчётов устройства. Это происходит за счёт повышения уровня математических моделей динамических систем,
принимающих участие в рассматриваемых технологиях. Получить “точные” решения
математических уравнений в аналитическом виде очень редко предоставляется
возможным, но даже существующие приближённые математические методы и
современные, практически неограниченные возможности электронно-вычислительной
техники позволяют ставить подобные задачи не на будущее, а решать их сегодня с
достаточной точностью.
В предлагаемой работе рассматривается
следующее устройство. На жесткой массивной раме 1, движущейся с поступательной
скоростью V0 консольно
закреплена призматическая упругая стойка 2 длинной L. На
другом конце стойки свободно вращается каток 3 радиусом R. Каток движется по поверхности почвы 4, которую следует
выровнять на расстоянии L+R−h от
точки крепления О консоли к раме (рис. 1).
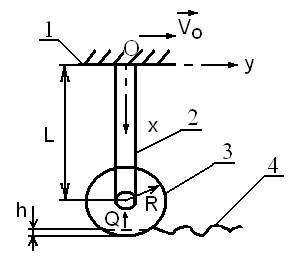
Рис. 1. Расчетная схема устройства
Усилия, возникающие в процессе функционирования
устройства незначительные, и позволяют с достаточной точностью пренебречь различного
рода нелинейными эффектами.
Рассмотрим уравнение Эйлера-Лагранжа для
функционала S [1]:
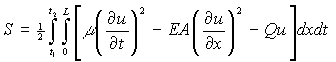 , (1)
, (1)
где µ −
погонная маса стержня;
А – площадь
поперечного сечения стержня;
E − модуль Юнга
материала;
Q − интенсивность внешней нагрузки.
Тогда динамическое уравнение имеет вид:
![]() (2)
(2)
Наличие катка массой М может быть учтено
краевыми условиями:
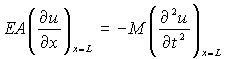 (3)
(3)
Стандартный расчёт подобных систем сводится к решению
частотного уравнения [1]:
![]()
![]()
![]()
![]() (4)
(4)
Решение приведено в [2].
Качественное
выравнивание почвы предполагает минимизацию рельефа после обработки. Сделаем
некоторые замечания относительно вида функции Q(t). Во-первых,
её вид зависит от применяемых ранее технологических операций. Иными словами, от
этих операций зависят параметры той функции, которой можна апроксимировать “рельеф”.
Безусловно, функция
рельефа является случайной и при выполнении условий Дирихле может быть
разложена в ряд Фурье:
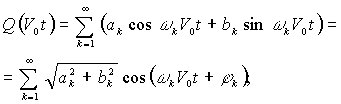 (5)
(5)
![]()
Применяя для каждой гармоники операционный метод и
приближая (5) ступенчатой функцией:
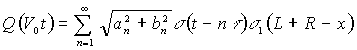 , (6)
, (6)
где σ(t) – ступенчатая
функция Хевисайда.
Получим:
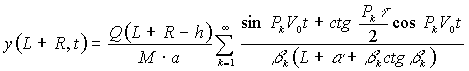 (7)
(7)
Здесь ![]() - амплитуда основной гармоники.
- амплитуда основной гармоники.
Дальнейшая
оптимизация устройства следует из минимизации выражения (7). Способов
минимизации, как и методов получения выражения типа (7) может быть довольно
много. Рассмотрим “минимизацию по полупериоду”, смысл которой сводится к следующему.
Интегрируя
выражение (7), определяем среднее значение выражения и производим минимизацию
среднего значения.
Получим:
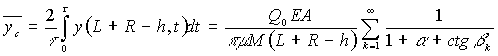 (8)
(8)
Дальнейшая
минимизация ![]() элементарна, особенно, если ограничится первыми членами
разложения ctg βk.
элементарна, особенно, если ограничится первыми членами
разложения ctg βk.
Литература:
1. Бабаков И.М.
Теория колебаний.−М., Наука, 1968;
2. Крылов А.Н.
Вибрации судов.−Изд. АН СССР, т. 10, 1948;
3. Бидерман В.Л. Прикладная теория механических колебаний.−М.,
Высшая школа, 1972;
4. Свешников А.А. Прикладные методы теории случайных функций.−М.,
Наука, 1968.