Николенко В.А.

Национальный технический университет Украины «Киевский политехнический институт», Украина

Реализация методики построения гибридных Байесовских сетей

Аннотация: исследовано различные методики построения гибридных Байесовских сетей. На основании проведенного исследования предложено методику построения гибридных Байесовских сетей и разработано программный продукт, реализующий данную методику. Проведено апробацию методики при построении Байесовской сети показателя ВВП Китая.

Ключевые слова: Байесовский подход, теория графов, гибридные сети, Байесовские сети, интеллектуальный анализ данных.

Введение. Технологическое развитие вычислительной техники последнего полувека характеризуется широким применением средств обработки цифровой информации, в различных сферах человеческой деятельности. При этом появился побочный продукт этой активности - сверхбольшие базы собранных данных.

Традиционная математическая статистика долгое время претендовала на роль основного инструмента анализа данных, но она не отвечала проблемам, которые возникали. Поэтому возникла необходимость в развитии новых современных методологий обработки и анализа данных. Такой новой методологии и стал интеллектуальный анализ данных (ИАД).

Технология ИАД (Data Mining) появилась в 1978 для решения задачи выявления скрытых взаимосвязей внутри больших баз данных. Большинство инструментов интеллектуального анализа данных основывается на двух технологиях: машинное обучение (machine learning) и визуализация (визуальное представление информации). Байесовские сети (БМ) как раз и сочетают в себе эти две технологии.

Это достаточно молодое направление развития науки, появившейся на стыке двух наук: теории вероятностей и теории графов (раздел дискретной математики). Идея внедрения БМ состоит в представлении причинно-следственных связей процесса в виде графа.

Байесовские сети (БС) представляют собой графические модели событий и процессов на основе объединения некоторых результатов теории вероятностей и теории графов. Они тесно связаны с диаграммами влияния, которые можно использовать для приятия решений. Несмотря на свое название, эти сети не обязательно подразумевают тесную связь с байесовскими методами. Название связано, прежде всего, с байесовским правилом вероятного вывода. БС представляют собой удобный инструмент для описания достаточно сложных процессов и событий с неопределенностями.

Гибридные БС - это сети, содержащие как узлы с дискретными переменными, так и с непрерывными.

Существуют различные методики построения гибридных БС, поэтому целесообразно определить наилучшую и реализовать ее в программном продукте. А также провести апробацию методики на основании данных такого макроэкономического показатель как ВВП, а именно ВВП Китая и США.

Особенности гибридных БС. Гибридная сеть Байеса Β = ( X , D, P) определяется через направленный ациклический граф G = ( X , E) и его функции , де — набор родительских узлов . X — набор переменных, разделенных на дискретные и непрерывные Г переменные, то есть . Структура графа ограничена тем, что непрерывные переменные не могут иметь дискретные переменные, как их узлы-потомки [1].

Исследование особенностей гибридных сетей Байеса показало, что гибридные сети являются обобщением обычных БМ для случаев, когда переменные в задаче имеют непрерывное распределение или очень большое количество возможных значений. Несмотря на сложность представления и формирования заключения в сети, гибридные сети целесообразно использовать для задач с большими объемами статистической информации.

Для гибридных сетей можно применять те же точные алгоритмы формирования выводов (алгоритм исключения переменной, передачи сообщения клик-дерева и т.п.), адаптируя их. Точный вывод в условных линейных гаусианах сложнее, чем в дискретных сетях Байеса. Поэтому неудивительно, что иногда приходится прибегать к приближенному алгоритму формирования вывода. При этом необходимо балансировать между необходимостью точного вывода и вычислительной сложности задачи, поскольку даже для простых структур сети, когда точный вывод в дискретных сетях может быть сформирован за линейное время, даже приближенный вывод гибридных моделях есть NP-сложной задачей.

Иногда есть смысл использовать дискретизацию непрерывных переменных при формировании вывода в гибридных сетях.

Этапы построения гибридной БС. Первый этап включает в себя построение структуры и оценивание параметров БС. Второй – построение вероятностного вывода БС. И, заключительный, третий – апробация модели на примерах анализа реальных статистических данных.

На сегодняшний день известно много методов решения задачи выбора оптимальной структуры сети Байеса. Оптимальной в том смысле, что выбранная структура МБ максимально правдоподобно будет отвечать процессу, который моделируется, или учебным данным. Вообще термин "построение сети Байеса" в англоязычной литературе в широком смысле означает реализацию таких процессов [2]:

а) поиск оптимальной структуры сети Байеса, то есть направленного ациклического графа, который наиболее адекватно соответствует учебным данным или исследуемом процесса;

б) вычисления значений таблиц условных вероятностей сети Байеса для узлов этого графа.

Большинство существующих методов построения структуры сети Байеса можно условно разделить на следующие категории [2]:

а) на основе оценочных функций (search & scoring): Чу и Лиу, Рибана и Перла, Кутато, К2 и т.д.;

б) применение тестов на условную независимость (dependency analysis): Вермута и Лоуренса, Перла, SRA и т.д.;

в) Методы для работы с неполными данными (когда часть данных отсутствует или некорректна): алгоритм максимизации математического ожидания, алгоритм сжатия границ.

Построение структуры БС состоит из двух подэтапов, причем на первом подэтапе возможны 2 случая (рис. 1).

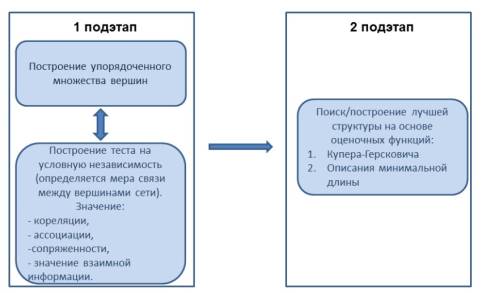
Рис. 1. Методы построения структуры (топологии) БС

В программном продукте был реализован алгоритм К2, предложенный Купером и Герсковичем, который выполняет поиск структуры с максимальным значением функции Купера-Герсковича. Для работы алгоритма нужно также иметь упорядоченное множество вершин [3].

Почти каждая система, которая использует сети Байеса, должна выполнять вероятностный вывод, то есть находить распределение определенных переменных при некоторых конкретных условиях. Для простых МБ разработаны точные и приближенные методы формирования вывода. Точные методы обычно дают точный результат, тогда как приближенные методы пытаются получить как можно ближе выходные данные. На практике существуют сети большого размера, для которых формирование точного заключения невозможно, поэтому применяют приближенные методы формирования выводу: отбора проб, выбора по значимости, взвешенной правдоподобия и другие.

Для приближенного к выводу наиболее известен стохастический отбор проб, он применяется для любого класса гибридных моделей.

Исследование показало, что одним из подходов к формированию выводу гибридной сети Байеса может быть предыдущая дискретизации непрерывных переменных (то есть сведения гибридной сети к дискретной) и использование известных алгоритмов формирования вывода для простых МБ.

Этот подход и был реализован в программном продукте, в силу своих преимуществ перед точными и приближенными методами формирования вывода. Идея заключается в разделении области каждой непрерывной переменной на некоторое определенное конечное число множеств. Например, такую непрерывную переменную, как возраст человека, можно разбить на 6 возрастных промежутков: 0-18, 18-25, 25-35, 35-50, 50-70, 70+. Таким образом, непрерывная переменная возраст представлена дискретной переменной, принимает одно из 6 значений. После чего условные вероятностные распределения дискретизируют и получают дискретную модель, с которой гораздо легче работать.

Наиболее известные методы дискретизации данных: иерархическая дискретизация, одинаковой ширины классов, равенство точек внутри классов.

В программном продукте было реализовано алгоритм Greedy Thick Thinning, который базируется на алгоритме К2, основанный на максимизации функции правдоподобия [4].

Анализ полученных результатов. В результате реализации методики построения гибридных БС было создано программный продукт, позволяющий строить гибридные БС. В качестве примера построения было выбрано сеть показателя ВВП Китая.

Для грамотного анализа данных было изучено теорию ВВП и определено, что для рационального анализа необходимо формализовать данные по арифметическим разницам (для расчета влияния факторов на отклонение результативного показателя).

При расчете ВВП в Китае учитывают следующие показатели: чистый экспорт (Net_export), потребительские расходы (Consumption_expenditure), расходы домохозяйств (Household_consumption_expenditure), правительственные расходы (Government_consumption_expenditure), внутренние инвестиции (Capital_formation), капитальные внутренние инвестиции (Fixed_capital_formation), добавленная стоимость (Value_added ), индекс сельского хозяйства (Agriculture), промышленность (Industry), строительное дело (Construction), торговля (Trade), транспорт (Transportation).

В качестве данных было выбрано показатель ВВП Китая за 1970 - 2013 г.г..

В результате получили БС ВВП Китая (рис. 2).

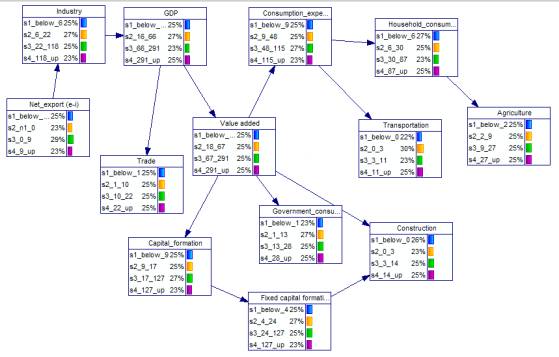
Рис. 2. Структура построенной БС для ВВП Китая

Проанализировав полученную сеть, можно сделать вывод, что полученная сеть соответствует нынешним реалиям экономики Китая. Как видим показатель ВВП имеет наиболее тесную связь со следующими показателями: добавленная стоимость (Value_added), промышленность (Industry), торговля (Trade). Это можно обосновать тем, что именно эти показатели занимают наибольшую долю в формирование ВВП Китая. Другие показатели ВВП также оказывают свое влияние и имеют соответствующие связи.

Заключение. Можем сделать вывод, что методика построения гибридной БС верна и дает нам точный и корректный результат. Выбранная методика построения гибридных БС состоит в следующем:

- на первом этапе происходит построение структуры и оценивание параметров (реализован алгоритм К2, который выполняет поиск структуры с максимальным значением функции Купера-Герсковича; для работы алгоритма нужно также иметь упорядоченное множество вершин);

- на втором этапе происходит формирование вероятностного вывода. Использовано методы формирования вывода, что и для обычных БС, но при условии предварительной дискретизации данных (реализовано алгоритм Greedy Thick Thinning, который базируется на алгоритме К2, основанный на максимизации функции правдоподобия).

Литература

1. Gogate, V. Approximate Inference Algorithms for Hybrid Bayesian Networks with Discrete Constraints / V. Gogate, R. Dechter // UAI. — 2005. — P. 209 — 216.

2. Згуровський М. З., Бідюк П. І., Терентьєв О. М., Просянкіна-Жарова Т. І. Байєсівські мережі в системах підтримки прийняття рішень — Київ : ТОВ «Видавниче Підприємство «Едельвейс», 2015. — 300 с.

3. Cooper G., Herskovits E. A Bayesian method for the induction of
probabilistic networks from data. // Machine Learning, 1992. – 9. – P. 309-347.

4. Smile — Structural Modelling, Inference, and Learning Engine [Электронный ресурс]. – Режим доступа:

http://smile.readthedocs.io/en/latest/greedythickthinning.html