Вариационное
генетическое программирование
для синтеза системы
управления робота
Ибадулла С.И.1, Дивеев А.И.2
1Кызылординский государственный университет имени
Коркыт Ата, (120000, Казахстан, ул.Тулькибаева 10), e-mail: sabit_sss@mail.ru
2Федеральное государственное бюджетное учреждение науки
Вычислительный центр им. А.А. Дородницына Российской академии наук, Москва,
Россия (119333, Москва, ул. Вавилова, 40), e-mail: aidiveev@mail.ru
В
последние два десятилетия область разработки и применения мобильных роботов
(МР) активно развивается. Благодаря небольшой массе, низкой стоимости, хорошей
гарантоспособности и гибким возможностям передвижения малые наземные роботы
стали мощным инструментом решения разнообразных задач многих направлений в
технике и научных исследованиях. Сегодня существует большое количество МР с
различными возможностями и дизайном (гусеничные, колесные, гибридные и др.),
[1] для которых ставятся и решаются задачи моделирования и синтеза системы
управления. Настоящая работа посвящена решению задачи синтеза управления МР.
Для данного вида решения задачи была разработана метод вариационного
генетического программирования.
Метод генетического
программирования [2] использует генетический алгоритм для строк символов. В
генетическом программировании символьная запись математического выражения
представляет собой бесскобочную строку символов. Каждый символ соответствует
некоторой операции или функции. Все функции характеризуется определенным
количеством аргументов. А функции без аргументов являются переменными или
параметрами. В настоящей работе представлена модификация метода генетического
программирования, метод вариационного генетического программирования [3].
Для кодирования
математических выражений введём множество упорядоченных наборов функций с
определённым количеством аргументов
, (1)
где
, 
, (2)
- функция под номером
с количеством
аргументов 
.
Математическое выражение
записываем в виде набора кодов функций
, (3)
где 
, 
- количество аргументов функции, 
- номер функции из
множества функций, 
,
Для определения
правильности записи функции введём понятие индекса для символа записи
математического выражения. Индекс 
символа 
математического
выражения (3) указывает на минимальное количество недостающих справа кодов
символов
, (4)
где
, 
, (5)
, (6)
- количество символов
в математическом выражении.
Поиск оптимального
математического выражения осуществляем методом малых вариаций базисного решения
(3). Для записи кода генетического программирования имеем пять малых вариаций:
0 – изменение значения второй компоненты кода элемента;
1 – удаление кода элемента с единичным значением первой компоненты;
2 – вставка в заданную позицию кода элемента с единичным значением первой
компоненты;
3 – увеличение значения первой компоненты кода элемента на единицу и
добавление в последнюю позицию кода с нулевым значением первой компоненты;
4 – уменьшение значения первой компоненты кода элемента на единицу и
Для описания малой
вариации используем вектор из трех компонент
, (7)
где 
- номер вариации, 
- номер варьируемого
элемента или позиция для вставки нового элемента, 
- значение второй
компоненты.
При решении задачи
синтеза управления методом вариационного генетического программирования
используем генетический алгоритм.
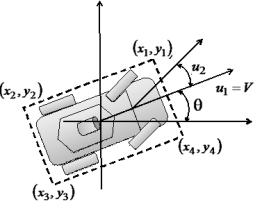
Пример. На рис. 1 приведена схема управления и геометрические параметры мобильного
робота.
Математическая модель объекта управления [4] имеет следующий вид:
, 
, 
,
где 
, 
- координаты центра
масс мобильного робота; 
- угол направления
вектора скорости, 
- обобщенный
габаритный параметр мобильного робота.
Рис. 1 Схема управления мобильным
роботом
На рис. 1 
, 
, 
, - координаты углов робота. Положение углов робота
определяются с помощью соотношений
,
, 
,
, 
,
, 
,
, 
,
, 
,
Значения управлений
ограничены 
, 
.
Задано множество
начальных условий
.
Задано терминальное
многообразие: 
, 
, 
,где 
, 
, 
- координаты
терминального положения центра масс робота.
Заданы пространственные
ограничения в виде логических функций
, 
,
где 
, 
, 
,
- число препятствий.
Необходимо найти
управление в форме функций от координат пространства состояний 
, 
.
Управление должно
обеспечивать перемещение робота из любого заданного в начального состояния в
терминальное положение, удовлетворяя ограничениям для углов робота за
минимальное время
. (8)
Для решения задачи
использовали вариационный генетический алгоритм. В численном эксперименте
использовали следующие значения параметров: 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
Множество начальных
значений имело следующий вид: 
. Терминальные условия имели значения: 
, 
, 
. Множество аргументов включало следующие элементы 
, где 
- числовые параметры,
которые также ищутся вместе со структурами функций .
Задаем базисное решение
в виде
, 
,
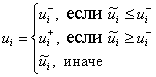где 
, 
, 
, 
, 
.
Для учета ограничения
использовали функцию штрафа,
, 
,
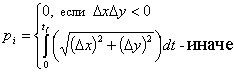где 
, 
.
При расчетах были
использованы следующие параметры генетического алгоритма: количество возможных
решений в начальной популяции 
; число поколений 128; число попыток скрещиваний в одном
поколении 512; число вариаций одного возможного решения 8; число бит для кода
целой части параметра 4; число бит для кода дробной части параметра 12; число
поколений между сменой базисного решения 24.
В результате синтеза
было получено следующее решение
, 
, 
,
.
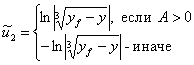На рис. 2-3 приведены
результаты моделирования синтезированной системы управления.
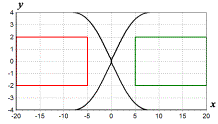
Рис. 2 Траектории движения центра масс объекта для различных начальных
состояний
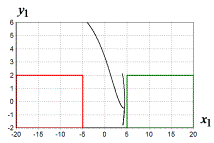
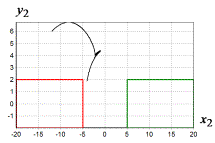
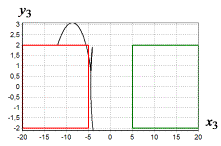
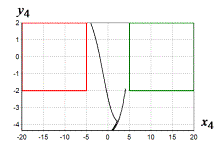
Рис. 3 Траектории движения углов
объекта для начального состояния 
, 
, 
Л и т е р
а т у р а
1.
Wong, J.Y. (Jo Yung). Theory of ground vehicles: 3rd ed. New
York: Wiley, 2001. 528 p.
2.
Koza J.R. Genetic Programming: On the Programming of
Computers by Means of Natural Selection. Cambridge, Massachusetts, London, MA:
MIT Press, 1992, 819 p.
3. Ибадулла С.И.,
Дивеев А.И., Софронова Е.А. Решение
задачи синтеза системы управления методом вариационного генетического
программирования // Современные проблемы науки и образования. 2013, № 6. http://www.science-education.ru/113-r11697
4.
Kentaro Oyama and Kenichiro Nonaka Model Predictive Parking Control for
Nonholonomic Vehicles using Time-State Control Form// 2013 European Control
Conference (ECC) July 17-19, 2013, Zürich, Switzerland. P. 458-465.
5.
Ибадулла С.И., Дивеев
А.И. Метод вариационного генетического программирования для синтеза систем
управления // Труды одиннадцатого международного симпозиума Интеллектуальные
системы INTELS’2014 под ред. К.А. Пупкова. – Москва. 30 июня – 04 июля. - 2014. - С. 74-77.
6.
9. Ибадулла С.И., Дивеев
А.И. Применение метода вариационного генетического
программирования для решения задачи синтеза управления мобильного робота //
Труды VII международная научно-практическая конференция. «Инженерные системы –
2014». – Москва, 16-18 апреля 2014г./ под общ.ред. Н.К. Пономорева. – М.: РУДН,
2014.- С. 6-10.
7.
14. Sager, Sebastian. A benchmark library of mixed-integer optimal
control problems // Mixed Integer Nonlinear Programming / ed. J. Lee and S. Leyffer. — 2012. - pp. 631–670.