Технические науки/2.Механика

D.of tech. sc. Artamonova E. N

Saratov State Technical University amed after Gagarin J.A., Russia

RELATIONS IN VISCOELASTICITY

In this article we propose a mathematical model of deformation and destruction elements, based on the relationship of both (macroscopic and microscopic) approaches allow for the dependence of the limiting critical conditions at which the destruction, the time of stress, temperature environmental exposure, exposure, etc. Physical relationships between stress and strain (constitutive equations) follow the principle of macroscopic definability [1, p. 295] and specified as the operator communication:

⦋

or

.

To close the equations of continuum mechanics must use the laws of thermodynamics, and other laws of physics for non-mechanical thermodynamic parameters.

t t

⦋, χ ⦋ - notation indicating the arguments in parentheses is in accordance with the

��=-∞ ��=-∞

postulate of the theory of simple materials, also satisfies the requirement of "decaying memory", ie materials, viscoelastic.

Operators t t

, χ - is the potential that is there are scalar operators that:

��=-∞ ��=-∞

= = ; (1)

ṿ = = . (2)

Physical relations (1, 2) – nonlinear, for description the strain state and fracture in the framework of a generalized model of inelasticity is necessary to consider the history of deformation of the sample depends on the loading path and on time.

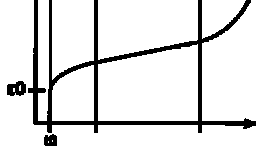
figure 1

Analysis of experimental data (fig.1) suggests characteristics of the temperature dependence of relaxation processes and fracture for viscoelastic polymers with the same value of energy activation for each material. Combining different approaches to describing these processes, i.e. formulation of a general mathematical theory of deformation and fracture of polymers depends on the study of the relationship of deformation, destruction and action of strain, temperature, aggressive factors in the whole time interval of operation of the element. Viscoelastic behavior reflects the combined viscous and elastic responses, under mechanical stress, of materials which are intermediate between liquids and solids in character. Viscoelastic Properties of Polymers examines, in detail, the effects of the many variables on which the basic viscoelastic properties depend. These include temperature, pressure, and time; polymer chemical composition, molecular weight and weight distribution, branching and crystallinity; dilution with solvents or plasticizers; and mixture with other materials to form composite systems.

According to (1, 2) can be written:

U - voltage potential (free energy).

= .

Deformation potential �� is determined by means of the Legendre transformation.

Way to represent U according to the hypothesis of memory:

(t, τ, ω);

Using the combined ratio of the basic laws of thermodynamics represent:

(τ)()≥ 0.

Consider different views . From the Stone-Weierstrass theorem continuous integral can be uniformly approximated by polynomials

U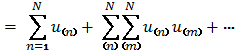, (3)

where the functionals can be represented as Stieltjes integrals:

= , (4)

- integrand. At τ ˂ 0 =0.

Substituting (4) (3) and differentiating with respect to e, we can obtain the relation between theory of Volterra-Frechet. The number of state parameters can be infinite, but the state of a thermodynamic system is defined by a finite number of parameters.

References:

1. Suvorova J.V., Ohlson N.G., Alexeeva S.I. An approach to the description of time-dependent materials // Materials and Design, Vol.24. Issue 4, June 2003. - P. 293-297.

2. Biing-Lin Lee, Lawrence E.N. Temperature Dependence of the Dynamic Mechanical Properties of Filled Polymers // J. of Polymer Science, Vol.15, 1977. - P.683-692.

3. Young J.F., Mindness S., Gray R.J. and Bentur A. The science and technology of civil engineering materials // Prentice Hall, 1998. - P.10-19.