А. Н. Хомченко

Черноморский государственный университет им. Петра Могилы,
г. Николаев, Украина

ЧЕТЫРЕ МОДИФИКАЦИИ ЭЛЕМЕНТА Н44

Введение. В семействе серендиповых конечных элементов высших порядков наиболее таинственным считается двумерный элемент четвертого порядка Q16 – quadrilateral с 16 узлами, расположенными на сторонах квадрата (включая вершины). Еще более загадочным является его трёхмерный аналог Н44-hexahedron с 44-мя узлами, равномерно расположенными на ребрах (включая вершины шестигранника). Информация о пространственных элементах высших порядков весьма ограничена, а об элементе Н44 она практически отсутствует. Правда, о специфических особенностях трехмерных моделей высших порядков некоторые авторы все же упоминают. Так, Норри и де Фриз[1], ссылаясь на Тейлора[2], утверждают, что на трехмерных элементах какие-либо модификации серендиповых базисов можно получить только путем использования дополнительных узлов (например, в центрах граней). К сожалению, этой точки зрения придерживаются многие специалисты, применяющие МКЭ. Нетрудно предположить, что большинство из них являются приверженцами методов матричной алгебры. Кстати, в случае с Н44 приходится составлять и решать СЛАУ 50х50. Между тем, за последние 40 лет (после публикаций Уачспресса) появились достаточно эффективные методы конструирования базисных функций (например, геометрические). Приведенные в статье 4 модели серендиповых базисов Н44 можно получить геометрически, используя фрагменты подходящих плоскостей и поверхностей. Это полезный способ конструирования и очень увлекательное занятие. Показывая четыре модификации базиса Н44, мы предлагаем читателю попытаться установить, из каких фрагментов составлена та или иная функция формы. Надеемся, что заинтересованные читатели смогут пополнить серендипово семейство новыми моделями.

Основная часть. На рис.1 показан конечный элемент Н44.

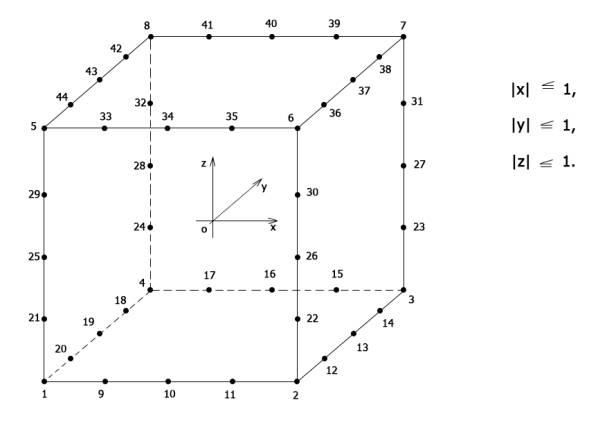
Рис. 1 Конечный элемент Н44.

Напомним, что базисные функции конечного элемента должны удовлетворять требованиям интерполяционной гипотезы Лагранжа.

,

где i – номер функции, k – номер узла. Чтобы составить полное представление о базисе Н44, достаточно писать только три функции: «узловую» (в вершине элемента) и «промежуточную» (в промежуточных узлах).

1-я модификация:

2-я модификация:

«центральные» функции во всех модификациях одинаковы.

3-я модификация (отличается от 1-й модификации только «промежуточными» функциями):

4-я модификация (отличается от 2-й модификации только «промежуточными» функциями):

,
i = 9, 11, 15, 17, 33, 35, 39, 41;

Множество других модификаций можно получить путем взвешенного усреднения известных модификаций.

Если пользоваться матричным методом, то после определения 50-ти базисных функций возникает задача устранения шести лишних функций и шести узлов. Речь идет о функциях, которые ассоциируются с узлами в серединах граней куба. Эту процедуру называют конденсацией. Геометрическое конструирование позволяет обойтись без конденсации.

Литература:

1. Нарри Д. Введение в метод конечных элементов / Д.Норри, Ж. де Фриз .- М.:Мир, 1981.-304с.

2. Taylor R.L. On the completeness of shape functions for finite element analysis / R.L. Taylor // Internat.J.Numer. Methods Eng .- 1972 .- v.4.-№1 .- P.17-22.