д.т.н.,
профессор. Пиль Э.А., Санкт-Петербургский государственный морской
технический университет,
область существования
экономической оболочки
В экономике часто встает вопрос, в каких
пределах может существовать экономика, чтобы не попасть в кризис. В данной
статье предлагаются графики, показывающие верхние и нижние области
существования экономической оболочки. Так на рис. 1 показаны две зависимости: Veuc
- максимальный объем
экономической оболочки, ед.3 и Velc - минимальный объем экономической оболочки, ед.3.
Как видно из рисунка здесь значения Veuc уменьшаются в 30 раз, а значения Velc
практически сливаются с осью Х, т.к. находятся в следующих пределах Velc = 0,08-0,258. Здесь следует сразу отметить, что все полученные
при расчетах значения Velc очень маленькие по сравнению с Velc.
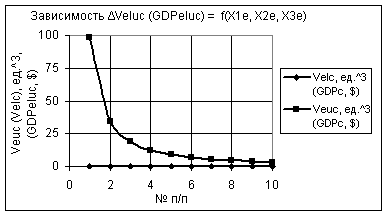
Рис. 1. Зависимости Veuc и Velc при Х1е = Х2е = 1, Х3е
= 10
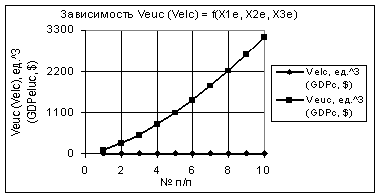
Рис. 2. Зависимости Veuc и Velc при Х1е = 1, Х2е = Х3е
= 10
Из следующего рис. 2 видно, что значения Veuc
увеличиваются по отношению к начальному в 31,62 раза. Если же все переменные
Х1е, Х2е и Х3е увеличатся в 10 раз, то в этом случае значение Veuc = 98124,68,
т.е. увеличится в 1000 раз, что и представлено на рис. 3.
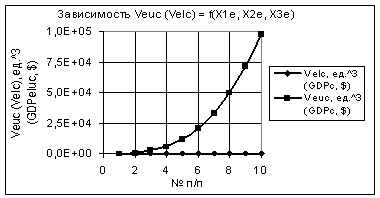
Рис. 3. Зависимости Veuc и Velc при Х1е = Х2е = Х3е =
10
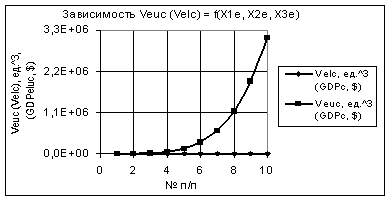
Рис. 4. Зависимости Veuc и Velc при Х1е = Х2е = 10,
Х3е = 1
При следующих значениях переменных Х1е = Х2е
= 10, Х3е = 1 величина Veuc достигнет еще большего значения Veuc = 3100000,
т.е. увеличится в 31593,97 раз.
Если же значения переменных будут
следующими: Х1е = Х3е = 10, Х2е = 1, то в этом случае построенные Veuc и Velc
представляют собой прямые линии, что и отображено на рис. 5.
Самые большие значения Veuc и Velc были
получены, когда переменные были следующими: Х1е = Х3е = 10, Х2е = 1…0,1 (см.
рис. 6).
На рис. 7 и 8 были получены зависимости,
имеющие максимумы.
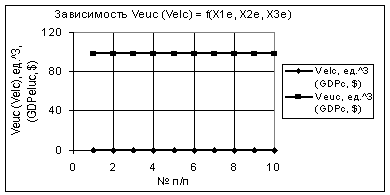
Рис. 5. Зависимости Veuc и Velc при Х1е = Х3е = 10,
Х2е = 1
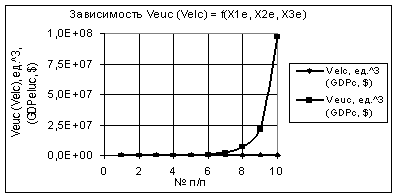
Рис. 6. Зависимости Veuc и Velc при Х1е = Х3е = 10,
Х2е = 1…0,1
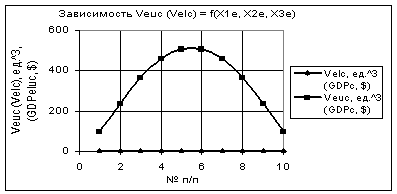
Рис. 7. Зависимости Veuc и Velc при Х1е = 10, Х2е =
Х3е = 1…0,1
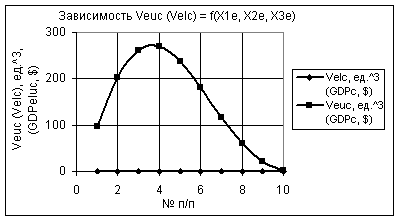
Рис. 8. Зависимости Veuc и Velc при Х1е = 10, Х2е =
Х3е = 1…0,1